
题目列表(包括答案和解析)
60.(09年吉林长春)26.如图,直线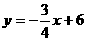 分别与x轴、y轴交于A、B两点;直线
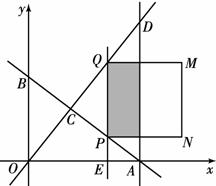
分别与x轴、y轴交于A、B两点;直线 与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿x轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).
与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿x轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).
(1)求点C的坐标.(1分)
(2)当0<t<5时,求S与t之间的函数关系式.(4分)
(3)求(2)中S的最大值.(2分)
(4)当t>0时,直接写出点(4,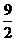 )在正方形PQMN内部时t的取值范围.(3分)
)在正方形PQMN内部时t的取值范围.(3分)
[参考公式:二次函数y=ax2+bx+c图象的顶点坐标为(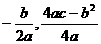 ).]
).]
(09年吉林长春26题解析)解:(1)由题意,得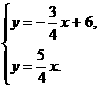 解得
解得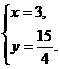
∴C(3,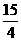 ).
(1分)
).
(1分)
(2)根据题意,得AE=t,OE=8-t.
∴点Q的纵坐标为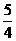 (8-t),点P的纵坐标为
(8-t),点P的纵坐标为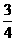 t,
t,
∴PQ=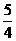 (8-t)-
(8-t)-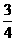 t=10-2t.
t=10-2t.
当MN在AD上时,10-2t=t,∴t=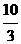 .
(3分)
.
(3分)
当0<t≤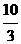 时,S=t(10-2t),即S=-2t2+10t.
时,S=t(10-2t),即S=-2t2+10t.
当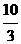 ≤t<5时,S=(10-2t)2,即S=4t2-40t+100.
(5分)
≤t<5时,S=(10-2t)2,即S=4t2-40t+100.
(5分)
(3)当0<t≤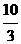 时,S=-2(t-
时,S=-2(t-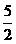 )2+
)2+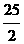 ,∴t=
,∴t=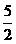 时,S最大值=
时,S最大值=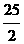 .
.
当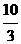 ≤t<5时,S=4(t-5)2,∵t<5时,S随t的增大而减小,
≤t<5时,S=4(t-5)2,∵t<5时,S随t的增大而减小,
∴t=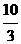 时,S最大值=
时,S最大值=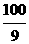 .
.
∵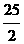 >
>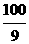 ,∴S的最大值为
,∴S的最大值为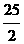 .
(7分)
.
(7分)
(4)4<t<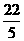 或t>6.
(10分)
或t>6.
(10分)
59.(09年湖南株洲)23.(本题满分12分)如图,已知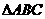 为直角三角形,
为直角三角形,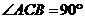 ,
,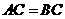 ,点
,点 、
、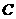 在
在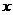 轴上,点
轴上,点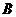 坐标为(
坐标为(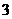 ,
, )(
)(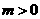 ),线段
),线段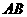 与
与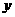 轴相交于点
轴相交于点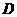 ,以
,以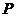 (1,0)为顶点的抛物线过点
(1,0)为顶点的抛物线过点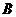 、
、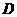 .
.
(1)求点 的坐标(用
的坐标(用 表示);
表示);
(2)求抛物线的解析式;
 (3)设点
(3)设点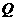 为抛物线上点
为抛物线上点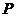 至点
至点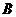 之间的一动点,连结
之间的一动点,连结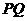 并延长交
并延长交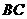 于点
于点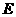 ,连结
,连结 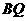 并延长交
并延长交 于点
于点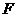 ,试证明:
,试证明: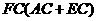 为定值.
为定值.
(09年湖南株洲23题解析)(1)由 可知
可知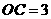 ,
,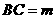 ,又△ABC为等腰直角三角形,∴
,又△ABC为等腰直角三角形,∴ ,
,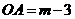 ,所以点A的坐标是(
,所以点A的坐标是(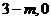 ).
………………… 3分
).
………………… 3分
(2)∵ ∴
∴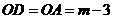 ,则点
,则点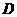 的坐标是(
的坐标是(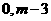 ).
).
又抛物线顶点为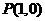 ,且过点
,且过点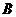 、
、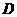 ,所以可设抛物线的解析式为:
,所以可设抛物线的解析式为: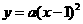 ,得:
,得:
 解得
解得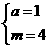 ∴抛物线的解析式为
∴抛物线的解析式为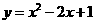 ………7分
………7分
(3)过点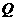 作
作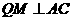 于点
于点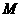 ,过点
,过点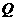 作
作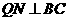 于点
于点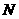 ,设点
,设点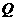 的坐标是
的坐标是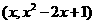 ,则
,则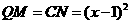 ,
, .
.
∵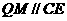 ∴
∴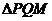 ∽
∽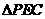 ∴
∴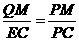 即
即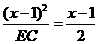 ,得
,得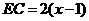
∵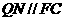 ∴
∴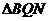 ∽
∽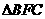 ∴
∴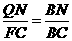 即
即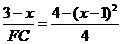 ,得
,得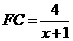
又∵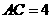
∴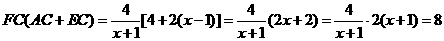
即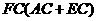 为定值8.
……………………12分
为定值8.
……………………12分
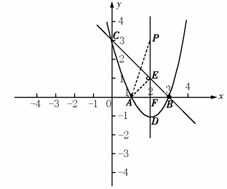
57.(09年湖南湘西自治州)25.(本题20分)在直角坐标系xoy中,抛物线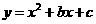 与x轴交于两点A、B,与y轴交于点C,其中A在B的左侧,B的坐标是(3,0).将直线
与x轴交于两点A、B,与y轴交于点C,其中A在B的左侧,B的坐标是(3,0).将直线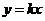 沿y轴向上平移3个单位长度后恰好经过点B、C.
沿y轴向上平移3个单位长度后恰好经过点B、C.
(1) 求k的值;
(2) 求直线BC和抛物线的解析式;
(3) 求△ABC的面积;
(4)  设抛物线顶点为D,点P在抛物线的对称轴上,且∠APD=∠ACB,求点P的坐标.
设抛物线顶点为D,点P在抛物线的对称轴上,且∠APD=∠ACB,求点P的坐标.
(09年湖南湘西自治州25题解析)解(1)直线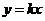 沿y轴向上平移3个单位后,过两点B,C
沿y轴向上平移3个单位后,过两点B,C
从而可设直线BC的方程为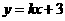 ············································································ 2分
············································································ 2分
令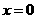 ,得C(0,3)································································································ 3分
,得C(0,3)································································································ 3分
又B(3,0)在直线上,
∴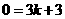
∴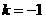 ······················································································································ 5分
······················································································································ 5分
(2)由(1),直线BC的方程为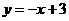 ·································································· 7分
·································································· 7分
又抛物线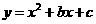 过点B,C
过点B,C
∴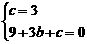
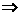
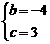
∴抛物线方程为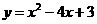 ··················································································· 10分
··················································································· 10分
(3)由(2),令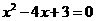
得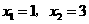 ·········································································································· 12分
·········································································································· 12分
即A(1,0),B(3,0),而C(0,3)
∴△ABC的面积S△ABC=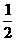 (3-1)·3=3平方单位··························································· 15分
(3-1)·3=3平方单位··························································· 15分
(4)由(2),D(2,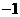 ),设对称轴与x轴交于点F,与BC交于E,可得E(2,1),
),设对称轴与x轴交于点F,与BC交于E,可得E(2,1),
连结AE.
∵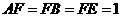
 ∴AE⊥CE,且AE=
∴AE⊥CE,且AE=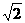 ,CE=
,CE=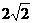
(或先作垂线AE⊥BC,再计算也可)
在Rt△AFP与Rt△AEC中,
∵∠ACE=∠APE(已知)
∴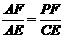 即
即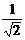 =
=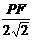
∴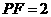 ······································································ 18分
······································································ 18分
∴点P的坐标为(2,2)或(2,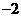 )·························· 20分
)·························· 20分
(x轴上、下方各一个)
(注:只有一个点扣1分)
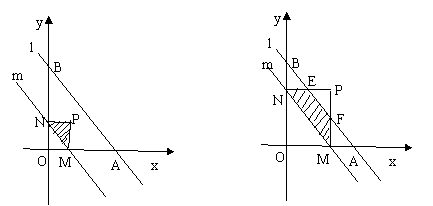
56.(09年湖南邵阳)25、如图(十二)直线l的解析式为y=-x+4, 它与x轴、y轴分
相交于A、B两点,平行于直线l的直线m从原点O出发,沿x
轴的正方向以每秒1个单位长度的速度运动,它与x轴、y轴分别
相交于M、N两点,运动时间为t秒(0<t≤4)
(1)求A、B两点的坐标;
(2)用含t的代数式表示△MON的面积S1;
(3)以MN为对角线作矩形OMPN,记 △MPN和△OAB重合部分的面积为S2 ;
当2<t≤4时,试探究S2 与之间的函数关系;
|
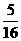 ?
?
(09年湖南邵阳25题解析)(1)当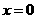 时,
时,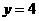 ;当
;当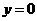 时,
时, .
.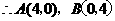 ; 2分
; 2分
(2)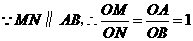 ,
,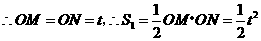 ;···· 4分
;···· 4分
(3)①当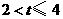 时,易知点
时,易知点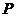 在
在 的外面,则点
的外面,则点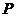 的坐标为
的坐标为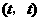 ,
,
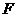 点的坐标满足
点的坐标满足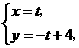 即
即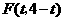 ,
,
同理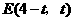 ,则
,则 ,··················································· 6分
,··················································· 6分
所以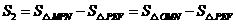
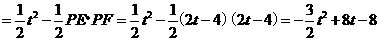 ;··································· 8分
;··································· 8分
②当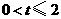 时,
时,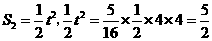 ,
,
解得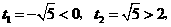 两个都不合题意,舍去;··········································· 10分
两个都不合题意,舍去;··········································· 10分
当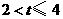 时,
时,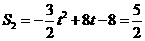 ,解得
,解得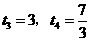 ,
,
综上得,当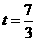 或
或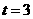 时,
时,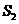 为
为 的面积的
的面积的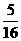 .·········································· 12分
.·········································· 12分
注:解答题用其它方法解答,请参照评分.
55.(09年湖南娄底)25.(本小题12分)如图11,在△ABC中,∠C=90°,BC=8,AC=6,另有一直角梯形DEFH
(HF∥DE,∠HDE=90°)的底边DE落在CB上,腰DH落在CA上,且DE=4,∠DEF=∠CBA,AH∶AC=2∶3
(1)延长HF交AB于G,求△AHG的面积.
(2)操作:固定△ABC,将直角梯形DEFH以每秒1个
单位的速度沿CB方向向右移动,直到点D与点B
重合时停止,设运动的时间为t秒,运动后的直角梯
形为DEFH′(如图12).
探究1:在运动中,四边形CDH′H能否为正方形?若能,
请求出此时t的值;若不能,请说明理由.
探究2:在运动过程中,△ABC与直角梯形DEFH′重叠
部分的面积为y,求y与t的函数关系.?
(09年湖南娄底25题解析)解:(1)∵AH∶AC=2∶3,AC=6
∴AH=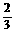 AC=
AC=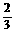 ×6=4
×6=4
又∵HF∥DE,∴HG∥CB,∴△AHG∽△ACB…………………………1分
∴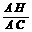 =
=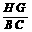 ,即
,即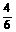 =
= ,∴HG=
,∴HG=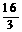 …………………………………2分
…………………………………2分
∴S△AHG=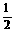 AH·HG=
AH·HG=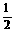 ×4×
×4×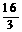 =
=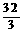 ……………………………………3分
……………………………………3分
(2)①能为正方形…………………………………………………………………4分
∵HH′∥CD,HC∥H′D,∴四边形CDH′H为平行四边形
又∠C=90°,∴四边形CDH′H为矩形…………………………………5分
又CH=AC-AH=6-4=2
∴当CD=CH=2时,四边形CDH′H为正方形
此时可得t=2秒时,四边形CDH′H为正方形…………………………6分
②(Ⅰ)∵∠DEF=∠ABC,∴EF∥AB
∴当t=4秒时,直角梯形的腰EF与BA重合.
当0≤t≤4时,重叠部分的面积为直角梯形DEFH′的面积.…………7分
过F作FM⊥DE于M,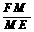 =tan∠DEF=tan∠ABC=
=tan∠DEF=tan∠ABC=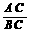 =
=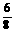 =
=
∴ME=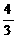 FM=
FM=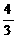 ×2=
×2=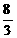 ,HF=DM=DE-ME=4-
,HF=DM=DE-ME=4-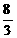 =
=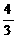
∴直角梯形DEFH′的面积为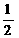 (4+
(4+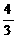 )×2=
)×2=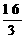
∴y=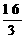 ………………………………………………………………8分
………………………………………………………………8分
(Ⅱ)∵当4<t≤5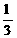 时,重叠部分的面积为四边形CBGH的面积-矩形CDH′H的面积.…………………………………………………………9分
时,重叠部分的面积为四边形CBGH的面积-矩形CDH′H的面积.…………………………………………………………9分
而S边形CBGH=S△ABC-S△AHG=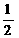 ×8×6-
×8×6-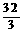 =
=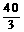
S矩形CDH′H?=2t
∴y=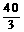 -2t……………………………………………………………………10分
-2t……………………………………………………………………10分
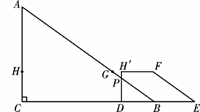 (Ⅲ)当5
(Ⅲ)当5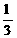 <t≤8时,如图,设H′D交AB
<t≤8时,如图,设H′D交AB
于P.
BD=8-t
又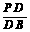 =tan∠ABC=
=tan∠ABC=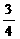
∴PD=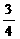 DB=
DB=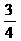 (8-t)………………11分
∴重叠部分的面积y=S??
(8-t)………………11分
∴重叠部分的面积y=S??
△PDB=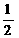 PD·DB
PD·DB
=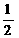 ·
·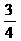 (8-t)(8-t)
(8-t)(8-t)
=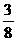 (8-t)2=
(8-t)2=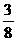 t2-6t+24
t2-6t+24
∴重叠部分面积y与t的函数关系式:

 y=
y=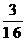 (0≤t≤4)
(0≤t≤4)
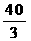 -2t(4<t≤5
-2t(4<t≤5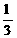 )
)
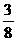 t2-6t+24(5
t2-6t+24(5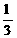 <t≤8)
<t≤8)
(注:评分时,考生未作结论不扣分)?
54.(09年湖南怀化)26. (本题满分10分)
如图12,在直角梯形OABC中, OA∥CB,A、B两点的坐标分别为A(15,0),B(10,12),动点P、Q分别从O、B两点出发,点P以每秒2个单位的速度沿OA向终点A运动,点Q以每秒1个单位的速度沿BC向C运动,当点P停止运动时,点Q也同时停止运动.线段OB、PQ相交于点D,过点D作DE∥OA,交AB于点E,射线QE交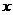 轴于点F.设动点P、Q运动时间为t(单位:秒).
轴于点F.设动点P、Q运动时间为t(单位:秒).
(1)当t为何值时,四边形PABQ是等腰梯形,请写出推理过程;
(2)当t=2秒时,求梯形OFBC的面积;
(3)当t为何值时,△PQF是等腰三角形?请写出推理过程.
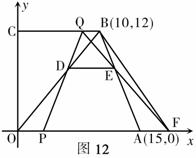
(09年湖南怀化26题解析)解:(1)如图4,过B作
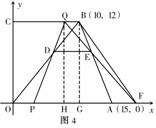 则
则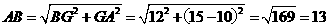 ······ (1分)
······ (1分)
过Q作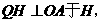
则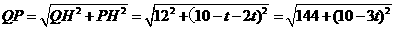
························································································· (2分)
要使四边形PABQ是等腰梯形,则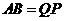 ,
,
即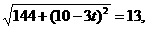
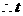
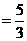 或
或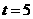 (此时
(此时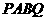 是平行四边形,不合题意,舍去)························· (3分)
是平行四边形,不合题意,舍去)························· (3分)
(2)当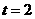 时,
时,
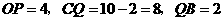 。
。
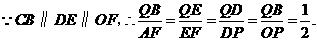 ··············································· (4分)
··············································· (4分)

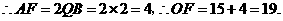 ···················································· (5分)
···················································· (5分)

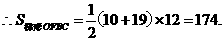 ··································································· (6分)
··································································· (6分)
(3)①当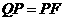 时,则
时,则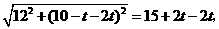
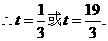 ···························································································· (7分)
···························································································· (7分)
②当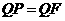 时,
时,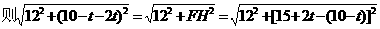
即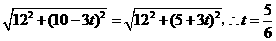 ······················································ (8分)
······················································ (8分)
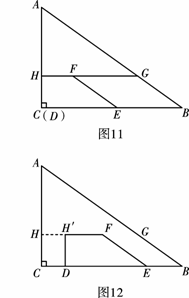 ③当
③当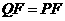 时,
时, 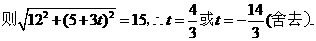 ········· (9分)
········· (9分)
综上,当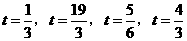 时,△PQF是等腰三角形.·············· (10分)
时,△PQF是等腰三角形.·············· (10分)
53.(09年湖南衡阳)26、(本小题满分9分)
如图12,直线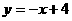 与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
(1)当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;
(2)当点M运动到什么位置时,四边形OCMD的面积有最大值?最大值是多少?
(3)当四边形OCMD为正方形时,将四边形OCMD沿着x轴的正方向移动,设平移的距离为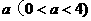 ,正方形OCMD与△AOB重叠部分的面积为S.试求S与
,正方形OCMD与△AOB重叠部分的面积为S.试求S与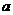 的函数关系式并画出该函数的图象.
的函数关系式并画出该函数的图象.


(09年湖南衡阳26题解析)(1)设点M的横坐标为x,则点M的纵坐标为-x+4(0<x<4,x>0,-x+4>0);
则:MC=∣-x+4∣=-x+4,MD=∣x∣=x;
∴C四边形OCMD=2(MC+MD)=2(-x+4+x)=8
∴当点M在AB上运动时,四边形OCMD的周长不发生变化,总是等于8;
(2)根据题意得:S四边形OCMD=MC·MD=(-x+4)· x=-x2+4x=-(x-2)2+4
∴四边形OCMD的面积是关于点M的横坐标x(0<x<4)的二次函数,并且当x=2,即当点M运动到线段AB的中点时,四边形OCMD的面积最大且最大面积为4;
(3)如图10(2),当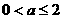 时,
时,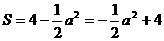 ;
;
如图10(3),当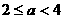 时,
时,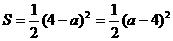 ;
;
∴S与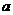 的函数的图象如下图所示:
的函数的图象如下图所示:


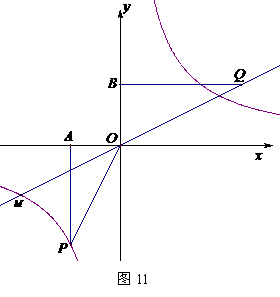
52.(09年湖南郴州)27. 如图11,已知正比例函数和反比例函数的图像都经过点M(-2,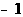 ),且P(
),且P(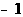 ,-2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.
,-2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.
(1)写出正比例函数和反比例函数的关系式;
(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;
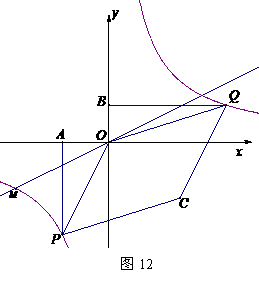
(3)如图12,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.
(09年湖南郴州27题解析)(1)设正比例函数解析式为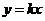 ,将点M(
,将点M(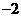 ,
,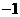 )坐标代入得
)坐标代入得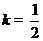 ,所以正比例函数解析式为
,所以正比例函数解析式为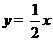 ······························································································ 2分
······························································································ 2分
同样可得,反比例函数解析式为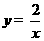 ···························································· 3分
···························································· 3分
(2)当点Q在直线DO上运动时,
设点Q的坐标为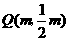 , ················································································ 4分
, ················································································ 4分
于是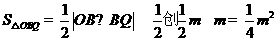 ,
,
而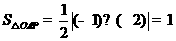 ,
,
所以有,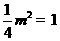 ,解得
,解得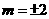 ········································································· 6分
········································································· 6分
所以点Q的坐标为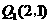 和
和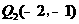 ······························································ 7分
······························································ 7分
(3)因为四边形OPCQ是平行四边形,所以OP=CQ,OQ=PC,
而点P(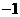 ,
,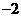 )是定点,所以OP的长也是定长,所以要求平行四边形OPCQ周长的最小值就只需求OQ的最小值.······························································································································ 8分
)是定点,所以OP的长也是定长,所以要求平行四边形OPCQ周长的最小值就只需求OQ的最小值.······························································································································ 8分
因为点Q在第一象限中双曲线上,所以可设点Q的坐标为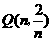 ,
,
由勾股定理可得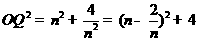 ,
,
所以当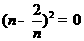 即
即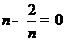 时,
时,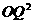 有最小值4,
有最小值4,
又因为OQ为正值,所以OQ与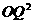 同时取得最小值,
同时取得最小值,
所以OQ有最小值2. ····························································································· 9分
由勾股定理得OP=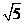 ,所以平行四边形OPCQ周长的最小值是
,所以平行四边形OPCQ周长的最小值是
 .······························································ 10分
.······························································ 10分
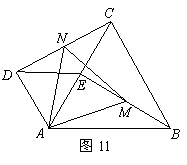
51.(09年湖南常德)26.如图9,若△ABC和△ADE为等边三角形,M,N分别EB,CD的中点,易证:CD=BE,△AMN是等边三角形.
(1)当把△ADE绕A点旋转到图10的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由;(4分)
(2)当△ADE绕A点旋转到图11的位置时,△AMN是否还是等边三角形?若是,请给出证明,并求出当AB=2AD时,△ADE与△ABC及△AMN的面积之比;若不是,请说明理由.(6分)

(09年湖南常德26题解析)解:(1)CD=BE.理由如下: 1分
∵△ABC和△ADE为等边三角形
∴AB=AC,AE=AD,∠BAC=∠EAD=60o
∵∠BAE =∠BAC-∠EAC =60o-∠EAC,
∠DAC =∠DAE-∠EAC =60o-∠EAC,
∴∠BAE=∠DAC, ∴△ABE ≌ △ACD·········································· 3分
∴CD=BE······························································· 4分
(2)△AMN是等边三角形.理由如下:·························· 5分
 ∵△ABE ≌ △ACD, ∴∠ABE=∠ACD.
∵△ABE ≌ △ACD, ∴∠ABE=∠ACD.
∵M、N分别是BE、CD的中点,
∴BM=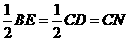
∵AB=AC,∠ABE=∠ACD, ∴△ABM ≌ △ACN.
∴AM=AN,∠MAB=∠NAC.··································· 6分
∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC=60o
∴△AMN是等边三角形.·········································· 7分
设AD=a,则AB=2a.
∵AD=AE=DE,AB=AC, ∴CE=DE.
∵△ADE为等边三角形, ∴∠DEC=120 o, ∠ADE=60o,
∴∠EDC=∠ECD=30o , ∴∠ADC=90o.·················································· 8分
∴在Rt△ADC中,AD=a,∠ACD=30 o , ∴ CD=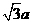 .
.
∵N为DC中点,
∴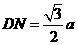 , ∴
, ∴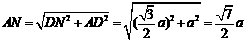 .························ 9分
.························ 9分
∵△ADE,△ABC,△AMN为等边三角形,
∴S△ADE∶S△ABC∶ S△AMN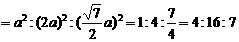 ························ 10分
························ 10分
解法二:△AMN是等边三角形.理由如下:··································································· 5分
∵△ABE ≌ △ACD,M、N分别是BE、CN的中点,∴AM=AN,NC=MB.
∵AB=AC,∴△ABM ≌ △ACN,∴∠MAB=∠NAC ,
∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC=60o
∴△AMN是等边三角形··························································································· 7分
设AD=a,则AD=AE=DE= a,AB=BC=AC=2a
易证BE⊥AC,∴BE=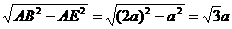 ,
,
∴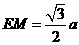 ∴
∴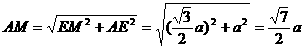
∵△ADE,△ABC,△AMN为等边三角形
∴S△ADE∶S△ABC∶ S△AMN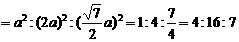 ···························· 10分
···························· 10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com