
题目列表(包括答案和解析)
46.(09年湖北武汉)25.(本题满分12分)
如图,抛物线 经过
经过 、
、 两点,与
两点,与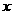 轴交于另一点
轴交于另一点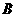 .
.
(1)求抛物线的解析式;
(2)已知点 在第一象限的抛物线上,求点
在第一象限的抛物线上,求点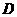 关于直线
关于直线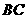 对称的点的坐标;
对称的点的坐标;
 (3)在(2)的条件下,连接
(3)在(2)的条件下,连接 ,点
,点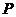 为抛物线上一点,且
为抛物线上一点,且 ,求点
,求点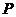 的坐标.
的坐标.
(09年湖北武汉25题解析)解:(1) 抛物线
抛物线 经过
经过 ,
, 两点,
两点,

解得
 抛物线的解析式为
抛物线的解析式为 .
.
 (2)
(2) 点
点 在抛物线上,
在抛物线上, ,
,
即 ,
, 或
或 .
.
 点
点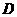 在第一象限,
在第一象限, 点
点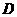 的坐标为
的坐标为 .
.
由(1)知 .
.
设点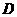 关于直线
关于直线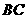 的对称点为点
的对称点为点 .
.
 ,
, ,且
,且 ,
,
 ,
,
 点在
点在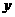 轴上,且
轴上,且 .
.

 ,
, .
.
即点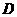 关于直线
关于直线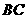 对称的点的坐标为(0,1).
对称的点的坐标为(0,1).
(3)方法一:作 于
于 ,
, 于
于 .
.
由(1)有: ,
,
 .
.
 ,
, 且
且 .
.
 ,
,
 .
.
 ,
, ,
, ,
,

 .
.
设 ,则
,则 ,
, ,
,
 .
.
 点在抛物线上,
点在抛物线上,

 ,
,
 (舍去)或
(舍去)或 ,
, .
.
方法二:过点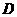 作
作 的垂线交直线
的垂线交直线 于点
于点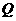 ,过点
,过点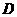 作
作 轴于
轴于 .过
.过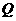 点作
点作 于
于 .
.
 .
.

 ,
,
又 ,
, .
.
 ,
, ,
, .
.
由(2)知 ,
, .
.
 ,
, 直线
直线 的解析式为
的解析式为 .
.
解方程组 得
得

 点
点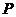 的坐标为
的坐标为 .
.
45.(09年湖北十堰)25.(12分)如图①, 已知抛物线 (a≠0)与
(a≠0)与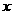 轴交于点A(1,0)和点B (-3,0),与y轴交于点C.
轴交于点A(1,0)和点B (-3,0),与y轴交于点C.
(1) 求抛物线的解析式;
 (2) 设抛物线的对称轴与
(2) 设抛物线的对称轴与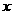 轴交于点M ,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
轴交于点M ,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
(3) 如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.

(09年湖北十堰25题解析)解: (1)由题知:  ……………………………………1 分
……………………………………1 分
解得:  ……………………………………………………………2分
……………………………………………………………2分
∴ 所求抛物线解析式为:  ……………………………3分
……………………………3分
(2) 存在符合条件的点P, 其坐标为P (-1,  )或P(-1,-
)或P(-1,-  )
)
或P (-1, 6) 或P (-1,  )………………………………………………………7分
)………………………………………………………7分
(3)解法①:
过点E 作EF⊥x 轴于点F , 设E ( a ,- -2a+3 )( -3< a < 0 )
-2a+3 )( -3< a < 0 )
∴EF=- -2a+3,BF=a+3,OF=-a ………………………………………………8
分
-2a+3,BF=a+3,OF=-a ………………………………………………8
分
∴S四边形BOCE
=  BF·EF
+
BF·EF
+  (OC +EF)·OF
(OC +EF)·OF
= ( a+3 )·(-
( a+3 )·(- -2a+3) +
-2a+3) +  (-
(- -2a+6)·(-a)……………………………9 分
-2a+6)·(-a)……………………………9 分
= ………………………………………………………………………10
分
………………………………………………………………………10
分
=-
 +
+
∴ 当a =- 时,S四边形BOCE
最大,
且最大值为
时,S四边形BOCE
最大,
且最大值为  .……………………………11 分
.……………………………11 分
此时,点E 坐标为 (- ,
, )……………………………………………………12分
)……………………………………………………12分
解法②:
过点E 作EF⊥x 轴于点F, 设E ( x , y ) ( -3< x < 0 ) …………………………8分
则S四边形BOCE
=  (3 + y )·(-x) +
(3 + y )·(-x) +  ( 3 + x )·y
………………………………………9分
( 3 + x )·y
………………………………………9分
=  ( y-x)=
( y-x)=  (
( ) …………………………………10 分
) …………………………………10 分
= -
 +
+ 
∴ 当x =- 时,S四边形BOCE
最大,且最大值为
时,S四边形BOCE
最大,且最大值为  . …………………………11分
. …………………………11分
此时,点E 坐标为 (- ,
, ) ……………………………………………………12分
) ……………………………………………………12分
说明:(1)抛物线解析式用其它形式表示,只要正确不扣分.
(2)直接应用公式法求抛物线顶点坐标或最大值不扣分.
(3)其它解法请参照评分说明给分.
44.(09年湖北荆门)25.(本题满分12分)一开口向上的抛物线与x轴交于A(m-2,0),B(m+2,0)两点,记抛物线顶点为C,且AC⊥BC.
(1)若m为常数,求抛物线的解析式;
(2)若m为小于0的常数,那么(1)中的抛物线经过怎么样的平移可以使顶点在坐标原点?
(3)设抛物线交y轴正半轴于D点,问是否存在实数m,使得△BCD为等腰三角形?若存在,求出m的值;若不存在,请说明理由.


(09年湖北荆门25题解析)解:(1)设抛物线的解析式为:y=a(x-m+2)(x-m-2)=a(x-m)2-4a.…………2分
∵AC⊥BC,由抛物线的对称性可知:△ACB是等腰直角三角形,又AB=4,
∴C(m,-2)代入得a= .∴解析式为:y=
.∴解析式为:y= (x-m)2-2.…………………………5分
(x-m)2-2.…………………………5分
(亦可求C点,设顶点式)
(2)∵m为小于零的常数,∴只需将抛物线向右平移-m个单位,再向上平移2个单位,可以使抛物线y= (x-m)2-2顶点在坐标原点.………………………………………7分
(x-m)2-2顶点在坐标原点.………………………………………7分
(3)由(1)得D(0, m2-2),设存在实数m,使得△BOD为等腰三角形.
m2-2),设存在实数m,使得△BOD为等腰三角形.
∵△BOD为直角三角形,∴只能OD=OB.……………………………………………9分
∴ m2-2=|m+2|,当m+2>0时,解得m=4或m=-2(舍).
m2-2=|m+2|,当m+2>0时,解得m=4或m=-2(舍).
当m+2<0时,解得m=0(舍)或m=-2(舍);
当m+2=0时,即m=-2时,B、O、D三点重合(不合题意,舍)
综上所述:存在实数m=4,使得△BOD为等腰三角形.……………………………12分
43.(09年湖北黄石)25.(本小题满分10分)
正方形 在如图所示的平面直角坐标系中,
在如图所示的平面直角坐标系中, 在
在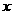 轴正半轴上,
轴正半轴上,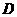 在
在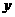 轴的负半轴上,
轴的负半轴上, 交
交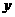 轴正半轴于
轴正半轴于 交
交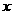 轴负半轴于
轴负半轴于 ,
, ,抛物线
,抛物线 过
过 三点.
三点.
(1)求抛物线的解析式;(3分)
(2)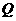 是抛物线上
是抛物线上 间的一点,过
间的一点,过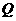 点作平行于
点作平行于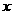 轴的直线交边
轴的直线交边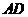 于
于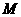 ,交
,交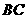 所在直线于
所在直线于 ,若
,若 ,则判断四边形
,则判断四边形 的形状;(3分)
的形状;(3分)
(3)在射线 上是否存在动点
上是否存在动点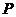 ,在射线
,在射线 上是否存在动点
上是否存在动点 ,使得
,使得 且
且 ,若存在,请给予严格证明,若不存在,请说明理由.(4分)
,若存在,请给予严格证明,若不存在,请说明理由.(4分)

(09年湖北黄石25题解析)解:(1)依条件有 ,
, .
.
 由
由 知
知 .
.
∴ 由
由 得
得 .
.
∴ .
.
将 的坐标代入抛物线方程,
的坐标代入抛物线方程,
得
 .
.
∴抛物线的解析式为 .····································································· 3分
.····································································· 3分
(2)设 ,
, ,
, .
.
∴
设 ,则
,则
∴
 ,
, (舍去
(舍去 )
)
此时点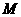 与点
与点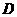 重合,
重合, ,
, ,
, ,
,
则 为等腰梯形.······························································································· 3分
为等腰梯形.······························································································· 3分
(3)在射线 上存在一点
上存在一点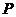 ,在射线
,在射线 上存在一点
上存在一点 .
.
使得 ,且
,且 成立,证明如下:
成立,证明如下:
当点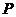 如图①所示位置时,不妨设
如图①所示位置时,不妨设 ,过点
,过点 作
作 ,
, ,
, ,垂足分别为
,垂足分别为 .
.
 若
若 .由
.由 得:
得:


 ,
,
 .
.
又

 .············································································································· 2分
.············································································································· 2分
当点 在如图②所示位置时,
在如图②所示位置时,
过点 作
作 ,
, ,
,
垂足分别为 .
.
同理可证 .
.
 .
.
又 ,
,
 ,
,
 .············································································································· 1分
.············································································································· 1分
当 在如图③所示位置时,过点
在如图③所示位置时,过点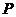 作
作 ,垂足为
,垂足为 ,
, 延长线,垂足为
延长线,垂足为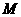 .
.
同理可证 .
.
 .············································································································· 1分
.············································································································· 1分
注意:分三种情况讨论,作图正确并给出一种情况证明正确的,同理可证出其他两种情况的给予4分;若只给出一种正确证明,其他两种情况未作出说明,可给2分,若用四点共圆知识证明且证明过程正确的也没有讨论三种情况的.只给2分.
42.(09年湖北黄冈) 20.(满分14分)如图,在平面直角坐标系xoy中,抛物线
20.(满分14分)如图,在平面直角坐标系xoy中,抛物线 与x轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动,线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
与x轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动,线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
(1)求A,B,C三点的坐标和抛物线的顶点的坐标;
(2)当t为何值时,四边形PQCA为平行四边形?请写出计算过程;
(3)当0<t< 时,△PQF的面积是否总为定值?若是,求出此定值,若不是,请说明理由;
时,△PQF的面积是否总为定值?若是,求出此定值,若不是,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?请写出解答过程.
(09年湖北黄冈20题解析)解:(1) ,令
,令 得
得 ,
,
∴ 或
或 ∴
∴ ;………………………1′
;………………………1′
在 中,令
中,令 得
得 即
即 ;………………2′
;………………2′
由于BC∥OA,故点C的纵坐标为-10,由 得
得 或
或
即 且易求出顶点坐标为
且易求出顶点坐标为 ……………………………………3′
……………………………………3′
于是, ,顶点坐标为
,顶点坐标为 。…………………4′
。…………………4′
(2)若四边形PQCA为平行四边形,由于QC∥PA。故只要QC=PA即可,而 故
故 得
得 ;……………………7′
;……………………7′
(3)设点P运动 秒,则
秒,则 ,
, ,说明P在线段OA上,且不与点OA、重合,
,说明P在线段OA上,且不与点OA、重合,
由于QC∥OP知△QDC∽△PDO,故
∴ ∴
∴ …………………9′
…………………9′
又点Q到直线PF的距离 ,∴
,∴ ,
,
于是△PQF的面积总为90。…………………………10′
(4)由上知, ,
, 。构造直角三角形后易得
。构造直角三角形后易得
 ,
,
①
若FP=PQ,即 ,故
,故 ,
,
∵ ∴
∴ ∴
∴ ……………………11′
……………………11′
②
若QP=QF,即 ,无
,无 的
的 满足条件;……………12′
满足条件;……………12′
③
若PQ=PF,即 ,得
,得 ,∴
,∴ 或
或 都不满足
都不满足 ,故无
,故无 的
的 满足方程;………………………13′
满足方程;………………………13′
综上所述:当 时,△PQR是等腰三角形。…………………………14′
时,△PQR是等腰三角形。…………………………14′
41.(09年湖北恩施州)24.如图,在 中,∠
中,∠
 °,
°, ,
,  的面积为
的面积为 ,点
,点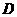 为
为 边上的任意一点(
边上的任意一点(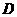 不与
不与 、
、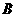 重合),过点
重合),过点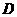 作
作 ∥
∥ ,交
,交 于点
于点 .设
.设 以
以 为折线将△
为折线将△ 翻折,所得的
翻折,所得的 与梯形
与梯形 重叠部分的面积记为y.
重叠部分的面积记为y.
 (1).用x表示∆ADE的面积;
(1).用x表示∆ADE的面积;
(2).求出 ﹤
﹤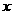 ≤
≤ 时y与x的函数关系式;
时y与x的函数关系式;
(3).求出 ﹤
﹤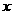 ﹤
﹤ 时y与x的函数关系式;
时y与x的函数关系式;
(4).当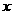 取何值时,
取何值时,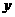 的值最大?最大值是多少?
的值最大?最大值是多少?

(09年湖北恩施州24题解析)解:(1) ∵ DE∥BC ∴∠ADE=∠B,∠AED=∠C
∴△ADE∽△ABC ∴

即 3分
3分
(2)∵BC=10 ∴BC边所对的三角形的中位线长为5
∴当0﹤ 时
时  6分
6分
(3) ﹤10时,点A'落在三角形的外部,其重叠部分为梯形
﹤10时,点A'落在三角形的外部,其重叠部分为梯形
∵S△A'DE=S△ADE=
 ∴DE边上的高AH=AH'=
∴DE边上的高AH=AH'=
由已知求得AF=5
∴A'F=AA'-AF=x-5
由△A'MN∽△A'DE知


∴ 9分
9分
(4)在函数 中
中
∵0﹤x≤5
∴当x=5时y最大为: 10分
10分
在函数
 中
中
当 时y最大为:
时y最大为: 11分
11分
∵ ﹤
﹤
∴当 时,y最大为:
时,y最大为: 12分
12分
40.(09年湖北鄂州)27.如图所示,将矩形OABC沿AE折叠,使点O恰好落在BC上F处,以CF为边作正方形CFGH,延长BC至M,使CM=|CF-EO|,再以CM、CO为边作矩形CMNO
(1)试比较EO、EC的大小,并说明理由
(2)令 ,请问m是否为定值?若是,请求出m的值;若不是,请说明理由
,请问m是否为定值?若是,请求出m的值;若不是,请说明理由
(3)在(2)的条件下,若CO=1,CE= ,Q为AE上一点且QF=
,Q为AE上一点且QF= ,抛物线y=mx2+bx+c经过C、Q两点,请求出此抛物线的解析式.
,抛物线y=mx2+bx+c经过C、Q两点,请求出此抛物线的解析式.
(4)在(3)的条件下,若抛物线y=mx2+bx+c与线段AB交于点P,试问在直线BC上是否存在点K,使得以P、B、K为顶点的三角形与△AEF相似?若存在,请求直线KP与y轴的交点T的坐标?若不存在,请说明理由。

(09年湖北鄂州27题解析)(1)EO>EC,理由如下:
由折叠知,EO=EF,在Rt△EFC中,EF为斜边,∴EF>EC, 故EO>EC …2分
(2)m为定值
∵S四边形CFGH=CF2=EF2-EC2=EO2-EC2=(EO+EC)(EO―EC)=CO·(EO―EC)
S四边形CMNO=CM·CO=|CE―EO|·CO=(EO―EC) ·CO
∴ ……………………………………………………4分
……………………………………………………4分
(3)∵CO=1, ∴EF=EO=
∴EF=EO=
∴cos∠FEC= ∴∠FEC=60°,
∴∠FEC=60°,
∴
∴△EFQ为等边三角形, …………………………………………5分
…………………………………………5分
作QI⊥EO于I,EI= ,IQ=
,IQ=
∴IO= ∴Q点坐标为
∴Q点坐标为 ……………………………………6分
……………………………………6分
∵抛物线y=mx2+bx+c过点C(0,1), Q ,m=1
,m=1
∴可求得 ,c=1
,c=1
∴抛物线解析式为 ……………………………………7分
……………………………………7分
(4)由(3),
 当
当 时,
时, <AB
<AB
∴P点坐标为 …………………8分
…………………8分
∴BP= AO
AO
方法1:若△PBK与△AEF相似,而△AEF≌△AEO,则分情况如下:
① 时,
时, ∴K点坐标为
∴K点坐标为 或
或
② 时,
时, ∴K点坐标为
∴K点坐标为 或
或 …………10分
…………10分
故直线KP与y轴交点T的坐标为
 …………………………………………12分
…………………………………………12分
方法2:若△BPK与△AEF相似,由(3)得:∠BPK=30°或60°,过P作PR⊥y轴于R,则∠RTP=60°或30°
①当∠RTP=30°时,
②当∠RTP=60°时,
∴ ……………………………12分
……………………………12分
39.(09年黑龙江绥化)28.(本小题满分lO分)

(09年黑龙江绥化28题解析)


38.(09年黑龙江齐齐哈尔)28.(本小题满分10分)
直线 与坐标轴分别交于
与坐标轴分别交于 两点,动点
两点,动点 同时从
同时从 点出发,同时到达
点出发,同时到达 点,运动停止.点
点,运动停止.点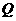 沿线段
沿线段 运动,速度为每秒1个单位长度,点
运动,速度为每秒1个单位长度,点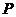 沿路线
沿路线 →
→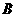 →
→ 运动.
运动.
(1)直接写出 两点的坐标;
两点的坐标;
(2)设点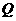 的运动时间为
的运动时间为 秒,
秒, 的面积为
的面积为 ,求出
,求出 与
与 之间的函数关系式;
之间的函数关系式;
 (3)当
(3)当 时,求出点
时,求出点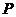 的坐标,并直接写出以点
的坐标,并直接写出以点 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点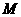 的坐标.
的坐标.
(09年黑龙江齐齐哈尔28题解析)(1)A(8,0)B(0,6)···································· 1分
(2)

 点
点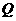 由
由 到
到 的时间是
的时间是 (秒)
(秒)
 点
点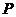 的速度是
的速度是 (单位/秒)·· 1分
(单位/秒)·· 1分
当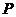 在线段
在线段 上运动(或0
上运动(或0 )时,
)时,
 ··························································································································· 1分
··························································································································· 1分
当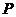 在线段
在线段 上运动(或
上运动(或 )时,
)时, ,
,
如图,作 于点
于点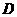 ,由
,由 ,得
,得 ,··································· 1分
,··································· 1分
 ·················································································· 1分
·················································································· 1分
(自变量取值范围写对给1分,否则不给分.)
(3) ··········································································································· 1分
··········································································································· 1分
 ···························································· 3分
···························································· 3分
注:本卷中各题,若有其它正确的解法,可酌情给分.
37.(09年黑龙江牡丹江)28.(本小题满分8分)
如图, 在平面直角坐标系中,
在平面直角坐标系中, 若
若 、
、 的长是关于
的长是关于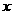 的一元二次方程
的一元二次方程 的两个根,且
的两个根,且
(1)求 的值.
的值.
(2)若 为
为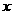 轴上的点,且
轴上的点,且 求经过
求经过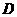 、
、 两点的直线的解析式,并判断
两点的直线的解析式,并判断 与
与 是否相似?
是否相似?
 (3)若点
(3)若点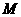 在平面直角坐标系内,则在直线
在平面直角坐标系内,则在直线 上是否存在点
上是否存在点 使以
使以 、
、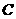 、
、 、
、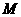 为顶点的四边形为菱形?若存在,请直接写出
为顶点的四边形为菱形?若存在,请直接写出 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
(09年黑龙江牡丹江28题解析)解:(1)解 得
得

 ··························································································· 1分
··························································································· 1分
在 中,由勾股定理有
中,由勾股定理有
 ···················································································· 1分
···················································································· 1分
(2)∵点 在
在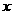 轴上,
轴上,


 ···················································································· 1分
···················································································· 1分
由已知可知D(6,4)
设 当
当 时有
时有
 解得
解得

 ····························································································· 1分
····························································································· 1分
同理 时,
时, ································································ 1分
································································ 1分
在 中,
中,
在 中,
中,

 ························································································ 1分
························································································ 1分
(3)满足条件的点有四个
 ·································· 4分
·································· 4分
说明:本卷中所有题目,若由其它方法得出正确结论,可参照本评分标准酌情给分.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com