
题目列表(包括答案和解析)
30.(09年贵州黔东南州)26、(12分)已知二次函数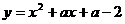 。
。
(1)求证:不论a为何实数,此函数图象与x轴总有两个交点。
(2)设a<0,当此函数图象与x轴的两个交点的距离为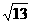 时,求出此二次函数的解析式。
时,求出此二次函数的解析式。
(3)若此二次函数图象与x轴交于A、B两点,在函数图象上是否存在点P,使得△PAB的面积为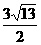 ,若存在求出P点坐标,若不存在请说明理由。
,若存在求出P点坐标,若不存在请说明理由。
(09年贵州黔东南州26题解析)解(1)因为△=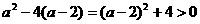
所以不论a为何实数,此函数图象与x轴总有两个交点。…………(2分)
(2)设x1、x2是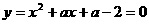 的两个根,则
的两个根,则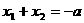 ,
,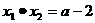 ,因两交点的距离是
,因两交点的距离是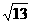 ,所以
,所以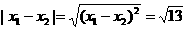 。…………(4分)
。…………(4分)
即: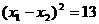
变形为: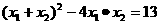 ……………………………………(5分)
……………………………………(5分)
所以:
整理得: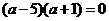
解方程得:
又因为:a<0
所以:a=-1
所以:此二次函数的解析式为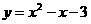 …………………………(6分)
…………………………(6分)
(3)设点P的坐标为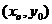 ,因为函数图象与x轴的两个交点间的距离等于
,因为函数图象与x轴的两个交点间的距离等于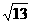 ,所以:AB=
,所以:AB=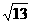 ……………………………………………………………………(8分)
……………………………………………………………………(8分)
所以:S△PAB=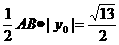
所以: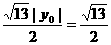
即: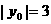 ,则
,则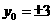 …………………………………(10分)
…………………………………(10分)
当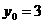 时,
时,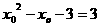 ,即
,即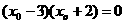
解此方程得: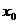 =-2或3
=-2或3
当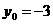 时,
时,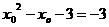 ,即
,即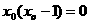
解此方程得: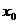 =0或1……………………………………(11分)
=0或1……………………………………(11分)
综上所述,所以存在这样的P点,P点坐标是(-2,3), (3,3), (0, -3)或(1, -3)。…(12分)
29.(09年广西梧州)26.(本题满分12分)
如图(9)-1,抛物线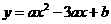 经过A(
经过A(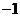 ,0),C(3,
,0),C(3,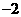 )两点,与
)两点,与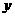 轴交于点D,与
轴交于点D,与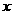 轴交于另一点B.
轴交于另一点B.
(1)求此抛物线的解析式;
(2)若直线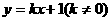 将四边形ABCD面积二等分,求
将四边形ABCD面积二等分,求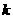 的值;
的值;
(3)如图(9)-2,过点E(1,1)作EF⊥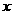 轴于点F,将△AEF绕平面内某点旋转180°得△MNQ(点M、N、Q分别与点A、E、F对应),使点M、N在抛物线上,作MG⊥
轴于点F,将△AEF绕平面内某点旋转180°得△MNQ(点M、N、Q分别与点A、E、F对应),使点M、N在抛物线上,作MG⊥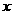 轴于点G,若线段MG︰AG=1︰2,求点M,N的坐标.
轴于点G,若线段MG︰AG=1︰2,求点M,N的坐标.
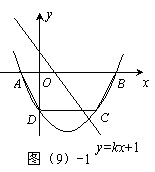
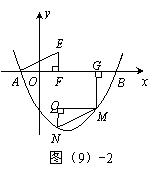
(09年广西梧州26题解析)(1)解:把A( ,0),C(3,
,0),C(3,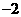 )代入抛物线
)代入抛物线 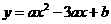 得
得
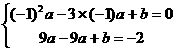 ················································································· 1分
················································································· 1分
整理得
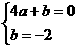 ………………
2分 解得
………………
2分 解得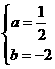 ………………3分
………………3分
∴抛物线的解析式为
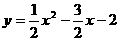 ··································································· 4分
··································································· 4分
(2)令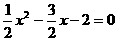 解得
解得 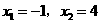
∴ B点坐标为(4,0)
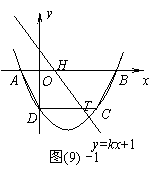 又∵D点坐标为(0,
又∵D点坐标为(0,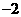 ) ∴AB∥CD ∴四边形ABCD是梯形.
) ∴AB∥CD ∴四边形ABCD是梯形.
∴S梯形ABCD =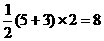 ···························· 5分
···························· 5分
设直线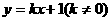 与x轴的交点为H,
与x轴的交点为H,
与CD的交点为T,
则H(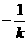 ,0), T(
,0), T(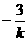 ,
,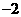 )··················· 6分
)··················· 6分
∵直线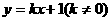 将四边形ABCD面积二等分
将四边形ABCD面积二等分
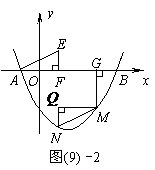 ∴S梯形AHTD =
∴S梯形AHTD =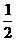 S梯形ABCD=4
S梯形ABCD=4
∴ ····································· 7分
····································· 7分
∴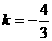 ···························································· 8分
···························································· 8分
(3)∵MG⊥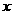 轴于点G,线段MG︰AG=1︰2
轴于点G,线段MG︰AG=1︰2
∴设M(m,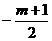 ),········································ 9分
),········································ 9分
∵点M在抛物线上 ∴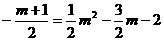
解得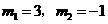 (舍去) ···························· 10分
(舍去) ···························· 10分
∴M点坐标为(3,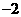 )····················································································· 11分
)····················································································· 11分
根据中心对称图形性质知,MQ∥AF,MQ=AF,NQ=EF,
∴N点坐标为(1,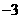 ) ···················································································· 12分
) ···················································································· 12分
28.(09年广西钦州)26.(本题满分10分)
如图,已知抛物线y=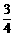 x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为(-1,0),过点C的直线y=
x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为(-1,0),过点C的直线y=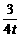 x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
(1)填空:点C的坐标是_▲_,b=_▲_,c=_▲_;
(2)求线段QH的长(用含t的式子表示);
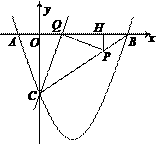 (3)依点P的变化,是否存在t的值,使以P、H、Q为顶点的三角形与△COQ相似?若存在,求出所有t的值;若不存在,说明理由.
(3)依点P的变化,是否存在t的值,使以P、H、Q为顶点的三角形与△COQ相似?若存在,求出所有t的值;若不存在,说明理由.
(09年广西钦州26题解析)解:(1)(0,-3),b=-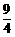 ,c=-3.·························· 3分
,c=-3.·························· 3分
 (2)由(1),得y=
(2)由(1),得y=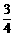 x2-
x2-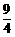 x-3,它与x轴交于A,B两点,得B(4,0).
x-3,它与x轴交于A,B两点,得B(4,0).
∴OB=4,又∵OC=3,∴BC=5.
由题意,得△BHP∽△BOC,
∵OC∶OB∶BC=3∶4∶5,
∴HP∶HB∶BP=3∶4∶5,
∵PB=5t,∴HB=4t,HP=3t.
∴OH=OB-HB=4-4t.
由y=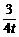 x-3与x轴交于点Q,得Q(4t,0).
x-3与x轴交于点Q,得Q(4t,0).
∴OQ=4t.··························································································· 4分
①当H在Q、B之间时,
QH=OH-OQ
=(4-4t)-4t=4-8t.································································ 5分
②当H在O、Q之间时,
QH=OQ-OH
=4t-(4-4t)=8t-4.································································ 6分
综合①,②得QH=|4-8t|;······························································· 6分
(3)存在t的值,使以P、H、Q为顶点的三角形与△COQ相似.··················· 7分
①当H在Q、B之间时,QH=4-8t,
若△QHP∽△COQ,则QH∶CO=HP∶OQ,得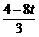 =
=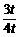 ,
,
∴t=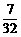 .···························································································· 7分
.···························································································· 7分
若△PHQ∽△COQ,则PH∶CO=HQ∶OQ,得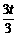 =
=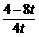 ,
,
即t2+2t-1=0.
∴t1=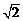 -1,t2=-
-1,t2=-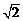 -1(舍去).················································· 8分
-1(舍去).················································· 8分
②当H在O、Q之间时,QH=8t-4.
若△QHP∽△COQ,则QH∶CO=HP∶OQ,得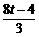 =
=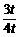 ,
,
∴t=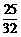 .···························································································· 9分
.···························································································· 9分
若△PHQ∽△COQ,则PH∶CO=HQ∶OQ,得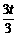 =
=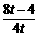 ,
,
即t2-2t+1=0.
∴t1=t2=1(舍去).·········································································· 10分
综上所述,存在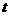 的值,t1=
的值,t1=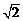 -1,t2=
-1,t2=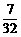 ,t3=
,t3=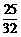 .························ 10分
.························ 10分
27.(09年广西南宁)26.如图14,要设计一个等腰梯形的花坛,花坛上底长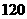 米,下底长
米,下底长 米,上下底相距
米,上下底相距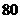 米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为
米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为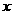 米.
米.
(1)用含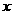 的式子表示横向甬道的面积;
的式子表示横向甬道的面积;
(2)当三条甬道的面积是梯形面积的八分之一时,求甬道的宽;
(3)根据设计的要求,甬道的宽不能超过6米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是5.7,花坛其余部分的绿化费用为每平方米0.02万元,那么当甬道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元?

(09年广西南宁26题解析)解:(1)横向甬道的面积为: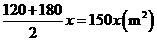 ·· 2分
·· 2分
(2)依题意: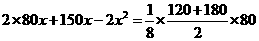 ·············································· 4分
·············································· 4分
整理得: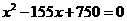
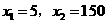 (不符合题意,舍去)······································································· 6分
(不符合题意,舍去)······································································· 6分
 甬道的宽为5米.
甬道的宽为5米.
(3)设建设花坛的总费用为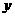 万元.
万元.
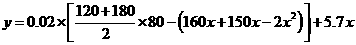 ············································ 7分
············································ 7分
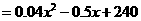
当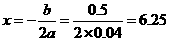 时,
时,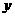 的值最小.··························································· 8分
的值最小.··························································· 8分
因为根据设计的要求,甬道的宽不能超过6米,
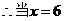 米时,总费用最少.······················································································ 9分
米时,总费用最少.······················································································ 9分
最少费用为: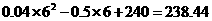 万元·················································· 10分
万元·················································· 10分
26.(09年广西柳州)26.(本题满分10分)
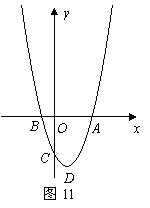
如图11,已知抛物线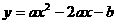 (
(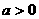 )与
)与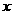 轴的一个交点为
轴的一个交点为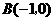 ,与y轴的负半轴交于点C,顶点为D.
,与y轴的负半轴交于点C,顶点为D.
(1)直接写出抛物线的对称轴,及抛物线与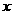 轴的另一个交点A的坐标;
轴的另一个交点A的坐标;
(2)以AD为直径的圆经过点C.
①求抛物线的解析式;
②点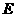 在抛物线的对称轴上,点
在抛物线的对称轴上,点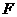 在抛物线上,且以
在抛物线上,且以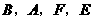 四点为顶点的四边形为平行四边形,求点
四点为顶点的四边形为平行四边形,求点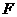 的坐标.
的坐标.
(09年广西柳州26题解析)解:(1)对称轴是直线: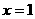 ,
,
点A的坐标是(3,0).···························································· 2分
(说明:每写对1个给1分,“直线”两字没写不扣分)
(2)如图11,连接AC、AD,过D作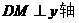 于点M,
于点M,
解法一:利用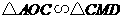
∵点A、D、C的坐标分别是A (3,0),D(1,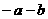 )、
)、
C(0,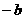 ),
),
∴AO=3,MD=1.
由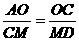 得
得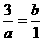
∴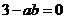 ··························································································· 3分
··························································································· 3分
又∵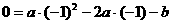 ······························································ 4分
······························································ 4分
∴由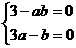 得
得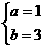 ································································ 5分
································································ 5分
∴函数解析式为: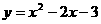 ······················································ 6分
······················································ 6分
解法二:利用以AD为直径的圆经过点C
∵点A、D的坐标分别是A (3,0) 、D(1,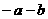 )、C(0,
)、C(0,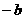 ),
),
∴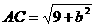 ,
,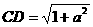 ,
,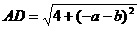
∵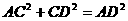
∴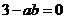 …① ·············································································· 3分
…① ·············································································· 3分
又∵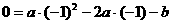 …② ···················································· 4分
…② ···················································· 4分
由①、②得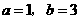 ·································································· 5分
·································································· 5分
∴函数解析式为: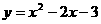 ··························································· 6分
··························································· 6分
(3)如图所示,当BAFE为平行四边形时
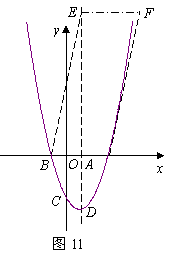 则
则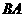 ∥
∥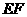 ,并且
,并且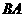 =
=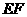 .
.
∵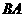 =4,∴
=4,∴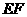 =4
=4
由于对称为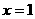 ,
,
∴点F的横坐标为5.·············································· 7分
将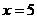 代入
代入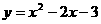 得
得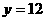 ,
,
∴F(5,12). ······················································· 8分
根据抛物线的对称性可知,在对称轴的左侧抛物线上也存在点F,使得四边形BAEF是平行四边形,此时点F坐标为(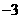 ,12). ··································································· 9分
,12). ··································································· 9分
当四边形BEAF是平行四边形时,点F即为点D,
此时点F的坐标为(1,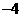 ). ································· 10分
). ································· 10分
综上所述,点F的坐标为(5,12), (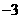 ,12)或(1,
,12)或(1,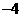 ).
).
(其它解法参照给分)
25.(09年广西贺州)28.(本题满分10分)如图,抛物线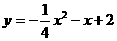 的顶点为A,与y 轴交于点B.
的顶点为A,与y 轴交于点B.
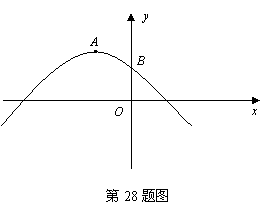 (1)求点A、点B的坐标.
(1)求点A、点B的坐标.
(2)若点P是x轴上任意一点,求证: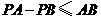 .
.
(3)当 最大时,求点P的坐标.
最大时,求点P的坐标.
(09年广西贺州28题解析)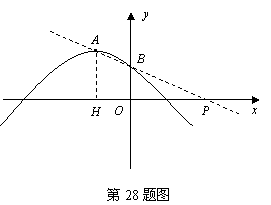 解:(1)抛物线
解:(1)抛物线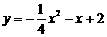 与y轴的交于点B,
与y轴的交于点B,
令x=0得y=2.
∴B(0,2) ············································· 1分
∵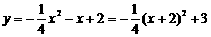
∴A(-2,3)··········································· 3分
(2)当点P是 AB的延长线与x轴交点时,
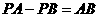 .············································· 5分
.············································· 5分
当点P在x轴上又异于AB的延长线与x轴的交点时,
在点P、A、B构成的三角形中, .
.
综合上述: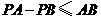 ················································································ 7分
················································································ 7分
(3)作直线AB交x轴于点P,由(2)可知:当PA-PB最大时,点P是所求的点 ····· 8分
作AH⊥OP于H.
∵BO⊥OP,
∴△BOP∽△AHP
∴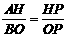 ····································································································· 9分
····································································································· 9分
由(1)可知:AH=3、OH=2、OB=2,
∴OP=4,故P(4,0) ··················································································· 10分
注:求出AB所在直线解析式后再求其与x轴交点P(4,0)等各种方法只要正确也相应给分.
2.第19题至第25题的其它解法,只要思路清晰,解法正确,都应按步骤给予相应分数.
2.求S2的值时,还可进行如下变形:
S2= S△PEF-S△OEF=S△PEF-(S四边形PEOF-S△PEF)=2 S△PEF-S四边形PEOF,再利用第(1)题中的结论.
注意:1.按照评分标准分步评分,不得随意变更给分点;
48.(09年湖北孝感)25.(本题满分12分)
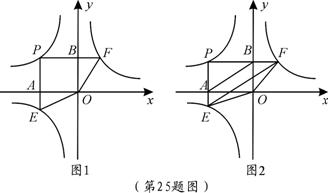
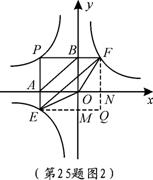
如图,点P是双曲线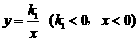 上一动点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交双曲线y=
上一动点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交双曲线y=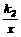 (0<k2<|k1|)于E、F两点.
(0<k2<|k1|)于E、F两点.
(1)图1中,四边形PEOF的面积S1= ▲ (用含k1、k2的式子表示);(3分)
(2)图2中,设P点坐标为(-4,3).
①判断EF与AB的位置关系,并证明你的结论;(4分)
②记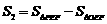 ,S2是否有最小值?若有,求出其最小值;若没有,请说明理由.(5分)
,S2是否有最小值?若有,求出其最小值;若没有,请说明理由.(5分)
(09年湖北孝感25题解析)解:(1)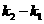 ;
…
………………………3分
;
…
………………………3分
(2)①EF∥AB. ……………………………………4分
证明:如图,由题意可得A(–4,0),B(0,3),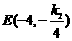 ,
,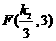 .
.
 ∴PA=3,PE=
∴PA=3,PE=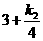 ,PB=4,PF=
,PB=4,PF=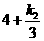 .
.
∴ ,
,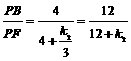
∴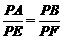 . ………………………… 6分
. ………………………… 6分
又∵∠APB=∠EPF.
∴△APB ∽△EPF,∴∠PAB=∠PEF.
∴EF∥AB. …………………………… 7分
②S2没有最小值,理由如下:
过E作EM⊥y轴于点M,过F作FN⊥x轴于点N,两线交于点Q.
由上知M(0,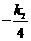 ),N(
),N(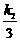 ,0),Q(
,0),Q(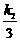 ,
,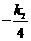 ). ……………… 8分
). ……………… 8分
而S△EFQ= S△PEF,
∴S2=S△PEF-S△OEF=S△EFQ-S△OEF=S△EOM+S△FON+S矩形OMQN
=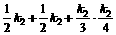
=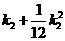
= .
………………………… 10分
.
………………………… 10分
当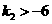 时,S2的值随k2的增大而增大,而0<k2<12. …………… 11分
时,S2的值随k2的增大而增大,而0<k2<12. …………… 11分
∴0<S2<24,s2没有最小值. …………………………… 12分
说明:1.证明AB∥EF时,还可利用以下三种方法.方法一:分别求出经过A、B两点和经过E、F两点的直线解析式,利用这两个解析式中x的系数相等来证明AB∥EF;方法二:利用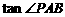 =
=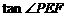 来证明AB∥EF;方法三:连接AF、BE,利用S△AEF=S△BFE得到点A、点B到直线EF的距离相等,再由A、B两点在直线EF同侧可得到AB∥EF.
来证明AB∥EF;方法三:连接AF、BE,利用S△AEF=S△BFE得到点A、点B到直线EF的距离相等,再由A、B两点在直线EF同侧可得到AB∥EF.
47.(09年湖北襄樊)26.(本小题满分13分)
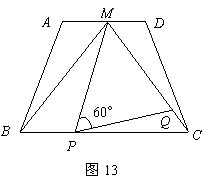
如图13,在梯形 中,
中,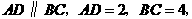 点
点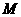 是
是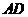 的中点,
的中点,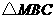 是等边三角形.
是等边三角形.
(1)求证:梯形 是等腰梯形;
是等腰梯形;
(2)动点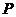 、
、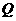 分别在线段
分别在线段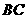 和
和 上运动,且
上运动,且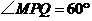 保持不变.设
保持不变.设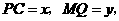 求
求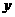 与
与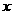 的函数关系式;
的函数关系式;
(3)在(2)中:①当动点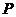 、
、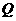 运动到何处时,以点
运动到何处时,以点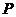 、
、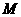 和点
和点 、
、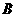 、
、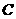 、
、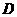 中的两个点为顶点的四边形是平行四边形?并指出符合条件的平行四边形的个数;
中的两个点为顶点的四边形是平行四边形?并指出符合条件的平行四边形的个数;
②当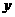 取最小值时,判断
取最小值时,判断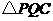 的形状,并说明理由.
的形状,并说明理由.
(09年湖北襄樊26题解析)(1)证明:∵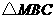 是等边三角形
是等边三角形
∴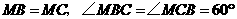 ·········· 1分
·········· 1分
∵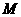 是
是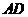 中点
中点
∴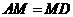
∵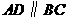
∴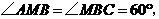
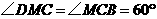
∴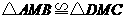 ·························· 2分
·························· 2分
∴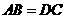
∴梯形 是等腰梯形.································································· 3分
是等腰梯形.································································· 3分
(2)解:在等边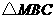 中,
中,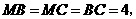
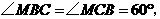
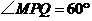
∴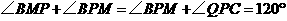
∴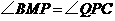 ······················································································· 4分
······················································································· 4分
∴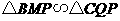 ∴
∴ ······························································ 5分
······························································ 5分
∵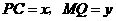 ∴
∴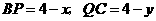 ·········································· 6分
·········································· 6分
∴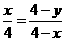 ∴
∴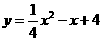 ··································································· 7分
··································································· 7分
(3)解:①当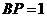 时,则有
时,则有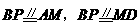
则四边形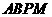 和四边形
和四边形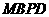 均为平行四边形
均为平行四边形
∴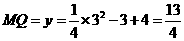 ··························································· 8分
··························································· 8分
当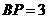 时,则有
时,则有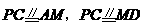
则四边形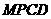 和四边形
和四边形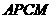 均为平行四边形
均为平行四边形
∴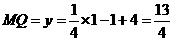 ······························································ 9分
······························································ 9分
∴当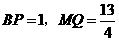 或
或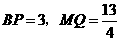 时,以P、M和A、B、C、 D中的两个点为顶点的四边形是平行四边形.
时,以P、M和A、B、C、 D中的两个点为顶点的四边形是平行四边形.
此时平行四边形有4个.····································································· 10分
②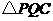 为直角三角形····································································· 11分
为直角三角形····································································· 11分
∵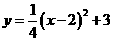
∴当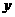 取最小值时,
取最小值时,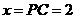 ························································ 12分
························································ 12分
∴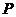 是
是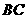 的中点,
的中点,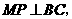 而
而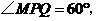
∴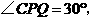 ∴
∴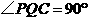 ······················································ 13分
······················································ 13分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com