
题目列表(包括答案和解析)
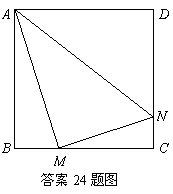
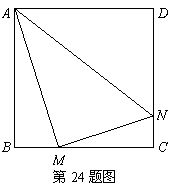
16.(09年广东汕头)24.(本题满分12分)正方形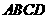 边长为4,
边长为4,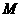 、
、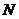 分别是
分别是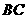 、
、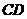 上的两个动点,当
上的两个动点,当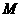 点在
点在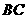 上运动时,保持
上运动时,保持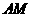 和
和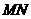 垂直,
垂直,
(1)证明: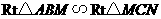 ;
;
(2)设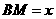 ,梯形
,梯形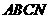 的面积为
的面积为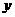 ,求
,求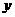 与
与 之间的函数关系式;当
之间的函数关系式;当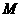 点运动到什么位置时,四边形
点运动到什么位置时,四边形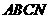 面积最大,并求出最大面积;
面积最大,并求出最大面积;
(3)当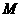 点运动到什么位置时
点运动到什么位置时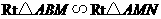 ,求
,求 的值.
的值.
(09年广东汕头24题解析)解:(1)在正方形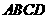 中,
中,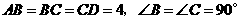 ,
,
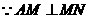 ,
,
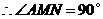 ,
,
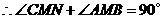 .
.
在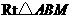 中,
中,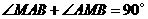 ,
,
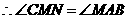 ,
,
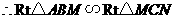 .·················································· 3分
.·················································· 3分
(2)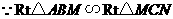 ,
,
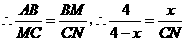 ,
,
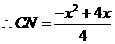 ,··········································································································· 5分
,··········································································································· 5分
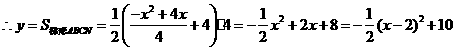 ,
,
当 时,
时,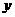 取最大值,最大值为10.············································································ 7分
取最大值,最大值为10.············································································ 7分
(3)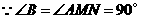 ,
,
 要使
要使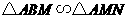 ,必须有
,必须有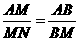 ,··························································· 9分
,··························································· 9分
由(1)知 ,
,
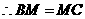 ,
,
 当点
当点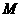 运动到
运动到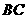 的中点时,
的中点时,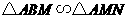 ,此时
,此时 .································· 12分
.································· 12分
(其它正确的解法,参照评分建议按步给分)
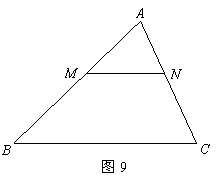
15.(09年广东清远)28.如图9,已知一个三角形纸片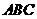 ,
,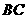 边的长为8,
边的长为8,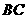 边上的高为
边上的高为 ,
,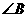 和
和 都为锐角,
都为锐角,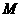 为
为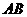 一动点(点
一动点(点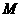 与点
与点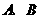 不重合),过点
不重合),过点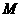 作
作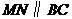 ,交
,交 于点
于点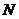 ,在
,在 中,设
中,设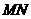 的长为
的长为 ,
,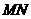 上的高为
上的高为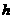 .
.
 (1)请你用含
(1)请你用含 的代数式表示
的代数式表示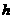 .
.
(2)将 沿
沿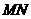 折叠,使
折叠,使 落在四边形
落在四边形 所在平面,设点
所在平面,设点 落在平面的点为
落在平面的点为 ,
,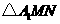 与四边形
与四边形 重叠部分的面积为
重叠部分的面积为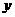 ,当
,当 为何值时,
为何值时,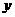 最大,最大值为多少?
最大,最大值为多少?
(09年广东清远28题解析)解:(1)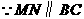
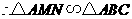
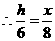
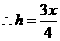 ······························································· 3分
······························································· 3分
(2)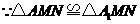
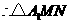 的边
的边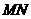 上的高为
上的高为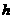 ,
,
 当点
当点 落在四边形
落在四边形 内或
内或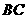 边上时,
边上时,
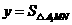 =
=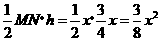 (0
(0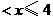 )··················································· 4分
)··················································· 4分
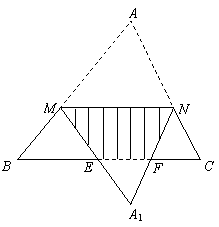
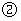 当
当 落在四边形
落在四边形 外时,如下图
外时,如下图 ,
,
设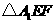 的边
的边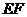 上的高为
上的高为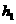 ,
,
则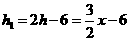
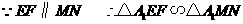
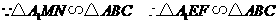
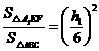
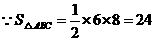
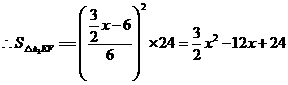
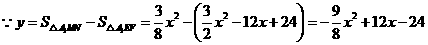
所以 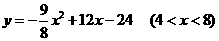 ······································································ 6分
······································································ 6分
综上所述:当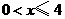 时,
时,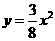 ,取
,取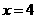 ,
,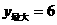
当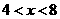 时,
时,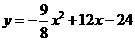 ,
,
取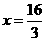 ,
,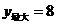
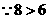
 当
当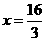 时,
时,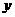 最大,
最大,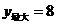 ··············································································· 8分
··············································································· 8分
14.(09年广东梅州)23.本题满分 11 分.
(提示:为了方便答题和评卷,建议在答题卡上画出你认为必须的图形)
如图 12,已知直线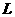 过点
过点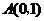 和
和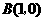 ,
,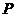 是
是 轴正半轴上的动点,
轴正半轴上的动点,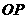 的垂直平分线交
的垂直平分线交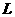 于点
于点 ,交
,交 轴于点
轴于点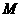 .
.
(1)直接写出直线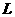 的解析式;
的解析式;
(2)设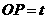 ,
,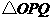 的面积为
的面积为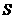 ,求
,求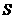 关于t的函数关系式;并求出当
关于t的函数关系式;并求出当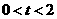 时,
时,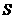 的最大值;
的最大值;
(3)直线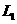 过点
过点 且与
且与 轴平行,问在
轴平行,问在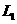 上是否存在点
上是否存在点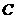 , 使得
, 使得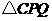 是以
是以 为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
(09年广东梅州23题解析)(1) ································································· 2分
································································· 2分
(2)∵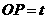 ,∴
,∴ 点的横坐标为
点的横坐标为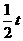 ,
,
①当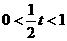 ,即
,即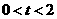 时,
时,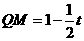 ,
,
∴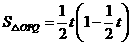 .····························································································· 3分
.····························································································· 3分
②当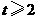 时,
时,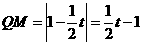 ,
,
∴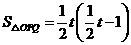 .
.
∴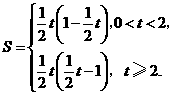 ······················································································· 4分
······················································································· 4分
当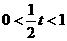 ,即
,即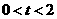 时,
时,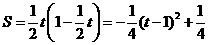 ,
,
∴当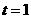 时,
时,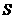 有最大值
有最大值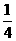 .······················································································ 6分
.······················································································ 6分
(3)由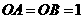 ,所以
,所以 是等腰直角三角形,若在
是等腰直角三角形,若在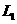 上存在点
上存在点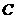 ,使得
,使得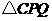 是以
是以 为直角顶点的等腰直角三角形,则
为直角顶点的等腰直角三角形,则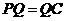 ,所以
,所以 ,又
,又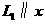 轴,则
轴,则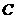 ,
, 两点关于直线
两点关于直线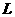 对称,所以
对称,所以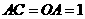 ,得
,得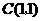 .···································································································································· 7
分
.···································································································································· 7
分
 下证
下证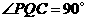 .连
.连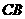 ,则四边形
,则四边形 是正方形.
是正方形.
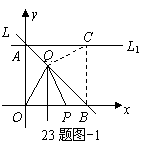
法一:(i)当点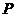 在线段
在线段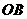 上,
上, 在线段
在线段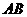 上
上
( 与
与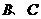 不重合)时,如图–1.
不重合)时,如图–1.
由对称性,得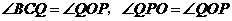 ,
,
∴  ,
,
∴ 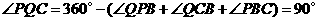 .············································· 8分
.············································· 8分
(ii)当点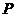 在线段
在线段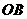 的延长线上,
的延长线上, 在线段
在线段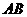 上时,如图–2,如图–3
上时,如图–2,如图–3
∵ , ∴
, ∴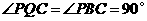 . ························ 9分
. ························ 9分
(iii)当点 与点
与点 重合时,显然
重合时,显然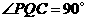 .
.
综合(i)(ii)(iii),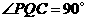 .
.
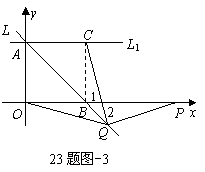 ∴在
∴在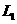 上存在点
上存在点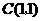 ,使得
,使得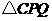 是以
是以 为直角顶点的等腰直角三角形.············ 11
分
为直角顶点的等腰直角三角形.············ 11
分
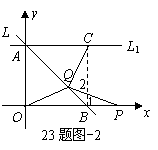
法二:由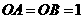 ,所以
,所以 是等腰直角三角形,若在
是等腰直角三角形,若在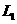 上存在点
上存在点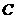 ,使得
,使得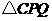 是以
是以 为直角顶点的等腰直角三角形,则
为直角顶点的等腰直角三角形,则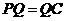 ,所以
,所以 ,又
,又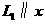 轴, 则
轴, 则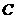 ,
, 两点关于直线
两点关于直线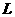 对称,所以
对称,所以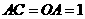 ,得
,得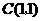 . ····················································································································· 7
分
. ····················································································································· 7
分
延长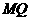 与
与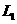 交于点
交于点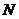 .
.
(i)如图–4,当点 在线段
在线段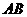 上(
上( 与
与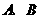 不重合)时,
不重合)时,
∵四边形 是正方形,
是正方形,
∴四边形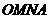 和四边形
和四边形 都是矩形,
都是矩形,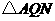 和
和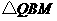 都是等腰直角三角形.
都是等腰直角三角形.
∴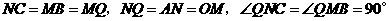 .
.
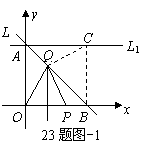 又∵
又∵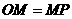 , ∴
, ∴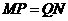 ,
,
∴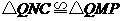 ,
,
∴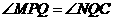 ,
,
又∵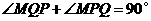 ,
,
∴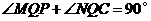 .
.
∴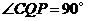 . ··································································································· 8分
. ··································································································· 8分
(ii)当点 与点
与点 重合时,显然
重合时,显然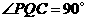 . ·········································· 9分
. ·········································· 9分
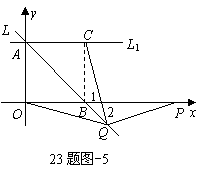
(iii) 在线段
在线段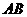 的延长线上时,如图–5,
的延长线上时,如图–5,
∵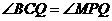 ,∠1=∠2
,∠1=∠2
∴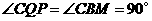
综合(i)(ii)(iii),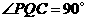 .
.
∴在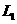 上存在点
上存在点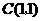 ,使得
,使得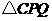 是以
是以 为直角顶点的等腰直角三角形. ······· 11分
为直角顶点的等腰直角三角形. ······· 11分
法三:由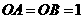 ,所以
,所以 是等腰直角三角形,若在
是等腰直角三角形,若在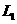 上存在点
上存在点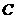 ,使得
,使得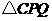 是以
是以 为直角顶点的等腰直角三角形,则
为直角顶点的等腰直角三角形,则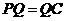 ,所以
,所以 ,又
,又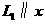 轴,
轴,
则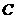 ,O两点关于直线
,O两点关于直线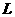 对称,所以
对称,所以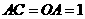 ,得
,得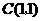 . ······················ 9分
. ······················ 9分
连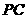 ,∵
,∵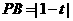 ,
, ,
,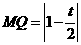 ,
,
∴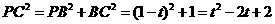 ,
,
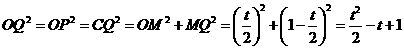 .
.
∴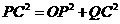 ,∴
,∴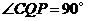 .································································· 10分
.································································· 10分
∴在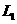 上存在点
上存在点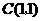 ,使得
,使得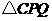 是以
是以 为直角顶点的等腰直角三角形. ··········· 11分
为直角顶点的等腰直角三角形. ··········· 11分
13.(09年广东茂名)25.(本题满分10分)
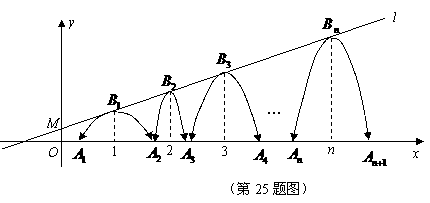
已知:如图,直线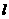 :
: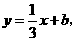 经过点
经过点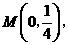 一组抛物线的顶点
一组抛物线的顶点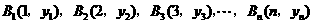 (
(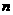 为正整数)依次是直线
为正整数)依次是直线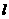 上的点,这组抛物线与
上的点,这组抛物线与 轴正半轴的交点依次是:
轴正半轴的交点依次是: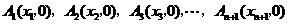 (
(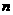 为正整数),设
为正整数),设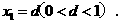
(1)求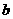 的值; (2分)
的值; (2分)
(2)求经过点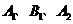 的抛物线的解析式(用含
的抛物线的解析式(用含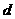 的代数式表示) (4分)
的代数式表示) (4分)
(3)定义:若抛物线的顶点与 轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为:“美丽抛物线”.
轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为:“美丽抛物线”.
探究:当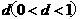 的大小变化时,这组抛物线中是否存在美丽抛物线?若存在,请你求出相应的
的大小变化时,这组抛物线中是否存在美丽抛物线?若存在,请你求出相应的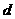 的值. (4分)
的值. (4分)
(09年广东茂名25题解析)解:(1)∵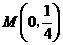 在
在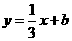 上,∴
上,∴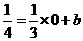 ,∴
,∴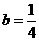 . 2分
. 2分
(2)由(1)得: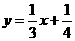 , ∵
, ∵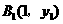 在
在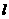 上,
上,
∴当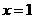 时,
时,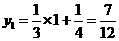 ,∴
,∴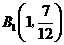 .········································· 3
分
.········································· 3
分
解法一:∴设抛物线表达式为: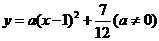 ,········································· 4分
,········································· 4分
又∵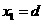 , ∴
, ∴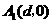 ,∴
,∴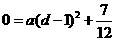 ,∴
,∴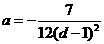 ,··············· 5
分
,··············· 5
分
∴经过点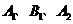 的抛物线的解析式为:
的抛物线的解析式为: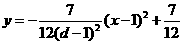 .············ 6
分
.············ 6
分
解法二:∵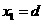 ,∴
,∴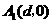 ,
,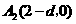 ,
,
∴设 ,········································································· 4
分
,········································································· 4
分
把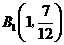 代入:
代入: ,得
,得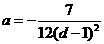 ,··························· 5
分
,··························· 5
分
∴抛物线的解析式为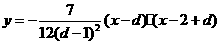 .·········································· 6
分
.·········································· 6
分
(3)存在美丽抛物线.······························································································· 7 分
由抛物线的对称性可知,所构成的直角三角形必是以抛物线顶点为直角顶点的等腰直角三角形,∴此等腰直角三角形斜边上的高等于斜边的一半,又∵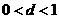 ,∴等腰直角三角形斜边的长小于2,∴等腰直角三角形斜边上的高必小于1,即抛物线的顶点的纵坐标必小于 1.
,∴等腰直角三角形斜边的长小于2,∴等腰直角三角形斜边上的高必小于1,即抛物线的顶点的纵坐标必小于 1.
∵当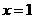 时,
时,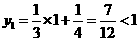 ,
,
当 时,
时,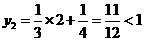 ,
,
当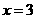 时,
时,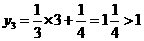 ,
,
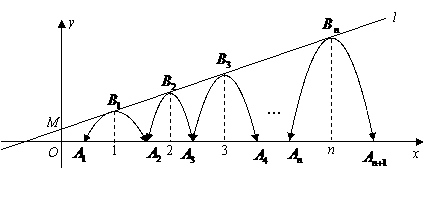
∴美丽抛物线的顶点只有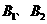 .··············································································· 8分
.··············································································· 8分
①若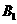 为顶点,由
为顶点,由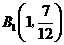 ,则
,则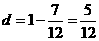 ;····················································· 9分
;····················································· 9分
②若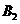 为顶点,由
为顶点,由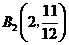 ,则
,则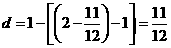 ,
,
综上所述,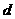 的值为
的值为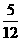 或
或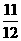 时,存在美丽抛物线.··················································· 10分
时,存在美丽抛物线.··················································· 10分
36.(09年黑龙江哈尔滨)28.(本题10分)
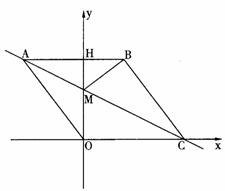
如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(-3,4),
点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H.
(1)求直线AC的解析式;
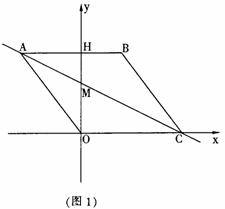
(2)连接BM,如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式(要求写出自变量t的取值范围);
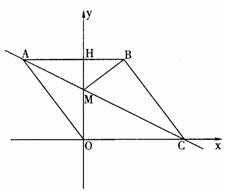
(3)在(2)的条件下,当 t为何值时,∠MPB与∠BCO互为余角,并求此时直线OP与直线AC所夹锐角的正切值.

(09年黑龙江哈尔滨28题解析)
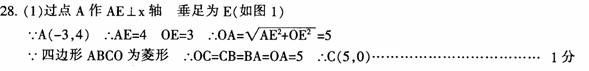
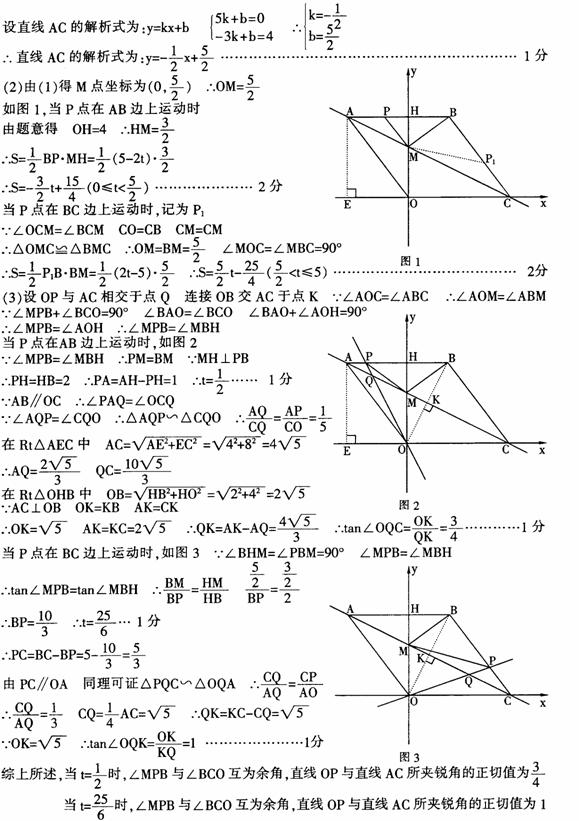
35.(09年河南)23.(11分)如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点.
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)动点P从点A出发.沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD
向终点D运动.速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于点E
①过点E作EF⊥AD于点F,交抛物线于点G.当t为何值时,线段EG最长?
②连接EQ.在点P、Q运动的过程中,判断有几个时刻使得△CEQ是等腰三角形?
请直接写出相应的t值.
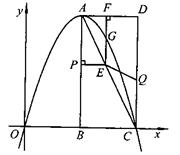
(09年河南23题解析)(1)点A的坐标为(4,8) …………………1分
将A (4,8)、C(8,0)两点坐标分别代入y=ax2+bx
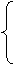 8=16a+4b
8=16a+4b
得
0=64a+8b
解 得a=-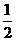 ,b=4
,b=4
∴抛物线的解析式为:y=-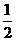 x2+4x
…………………3分
x2+4x
…………………3分
(2)①在Rt△APE和Rt△ABC中,tan∠PAE=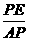 =
=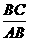 ,即
,即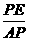 =
=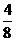
∴PE=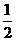 AP=
AP=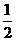 t.PB=8-t.
t.PB=8-t.
∴点E的坐标为(4+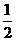 t,8-t).
t,8-t).
∴点G的纵坐标为:-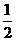 (4+
(4+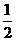 t)2+4(4+
t)2+4(4+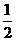 t)=-
t)=-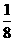 t2+8. …………………5分
t2+8. …………………5分
∴EG=-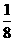 t2+8-(8-t)
t2+8-(8-t)
=-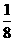 t2+t.
t2+t.
∵-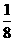 <0,∴当t=4时,线段EG最长为2.
…………………7分
<0,∴当t=4时,线段EG最长为2.
…………………7分
②共有三个时刻. …………………8分
t1=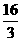 , t2=
, t2=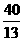 ,t3=
,t3= 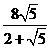 .
…………………11分
.
…………………11分
34.(09年河北)26.(本小题满分12分)如图16,在Rt△ABC中,∠C=90°,AC = 3,AB = 5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).
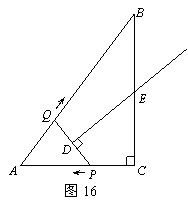 (1)当t
= 2时,AP = ,点Q到AC的距离是 ;
(1)当t
= 2时,AP = ,点Q到AC的距离是 ;
(2)在点P从C向A运动的过程中,求△APQ的面积S与
t的函数关系式;(不必写出t的取值范围)
(3)在点E从B向C运动的过程中,四边形QBED能否成
为直角梯形?若能,求t的值.若不能,请说明理由;
(4)当DE经过点C 时,请直接写出t的值.
(09年河北26题解析)解:(1)1,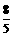 ;
;
(2)作QF⊥AC于点F,如图3, AQ = CP= t,∴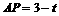 .
.
由△AQF∽△ABC,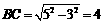 ,
,
得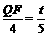 .∴
.∴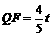 .
.
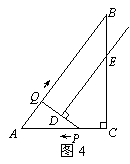 ∴
∴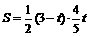 ,
,
即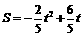 .
.
(3)能.
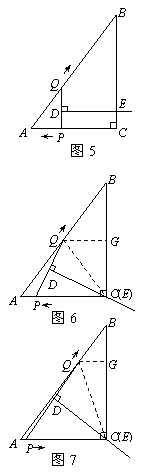
①当DE∥QB时,如图4.
∵DE⊥PQ,∴PQ⊥QB,四边形QBED是直角梯形.
此时∠AQP=90°.
 由△APQ ∽△ABC,得
由△APQ ∽△ABC,得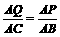 ,
,
即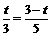 . 解得
. 解得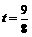 .
.
②如图5,当PQ∥BC时,DE⊥BC,四边形QBED是直角梯形.
此时∠APQ =90°.
由△AQP ∽△ABC,得 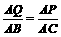 ,
,
即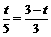 . 解得
. 解得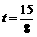 .
.
(4)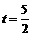 或
或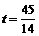 .
.
[注:①点P由C向A运动,DE经过点C.
方法一、连接QC,作QG⊥BC于点G,如图6.
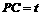 ,
,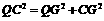
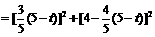 .
.
由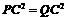 ,得
,得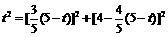 ,解得
,解得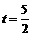 .
.
方法二、由 ,得
,得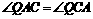 ,进而可得
,进而可得
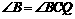 ,得
,得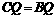 ,∴
,∴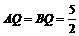 .∴
.∴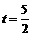 .
.
②点P由A向C运动,DE经过点C,如图7.
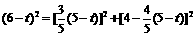 ,
,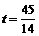 ]
]
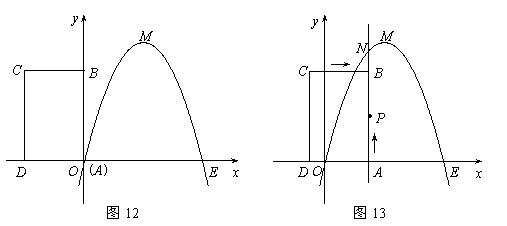
33.(09年海南)24.(满分13分)如图12,已知抛物线经过坐标原点O和x轴上另一点E,顶点M的坐标为 (2,4);矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3.
(1)求该抛物线所对应的函数关系式;
(2)将矩形ABCD以每秒1个单位长度的速度从图12所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图13所示).
①
当t=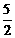 时,判断点P是否在直线ME上,并说明理由;
时,判断点P是否在直线ME上,并说明理由;
② 设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
(09年海南24题解析)(1)因所求抛物线的顶点M的坐标为(2,4),
故可设其关系式为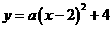 ………………(1分)
………………(1分)
又抛物线经过O(0,0),于是得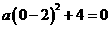 , ………………(2分)
, ………………(2分)
解得 a=-1 ………………(3分)
∴ 所求函数关系式为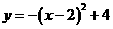 ,即
,即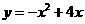 . ……………(4分)
. ……………(4分)
(2)① 点P不在直线ME上. ………………(5分)
根据抛物线的对称性可知E点的坐标为(4,0),
又M的坐标为(2,4),设直线ME的关系式为y=kx+b.
于是得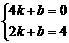 ,解得
,解得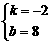
所以直线ME的关系式为y=-2x+8. ……(6分)
由已知条件易得,当t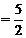 时,OA=AP
时,OA=AP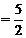 ,
,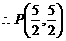 ……………(7分)
……………(7分)
∵ P点的坐标不满足直线ME的关系式y=-2x+8.
∴ 当t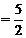 时,点P不在直线ME上.
………………(8分)
时,点P不在直线ME上.
………………(8分)
② S存在最大值. 理由如下: ………………(9分)
∵ 点A在x轴的非负半轴上,且N在抛物线上, ∴ OA=AP=t.
∴ 点P,N的坐标分别为(t,t)、(t,-t 2+4t) ∴ AN=-t 2+4t (0≤t≤3) ,
∴ AN-AP=(-t 2+4 t)- t=-t 2+3 t=t(3-t)≥0 , ∴ PN=-t 2+3 t …(10分)
(ⅰ)当PN=0,即t=0或t=3时,以点P,N,C,D为顶点的多边形是三角形,此三角形的高为AD,∴ S=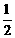 DC·AD=
DC·AD=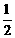 ×3×2=3. ………………(11分)
×3×2=3. ………………(11分)
(ⅱ)当PN≠0时,以点P,N,C,D为顶点的多边形是四边形
∵ PN∥CD,AD⊥CD,
∴ S=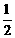 (CD+PN)·AD=
(CD+PN)·AD=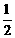 [3+(-t 2+3 t)]×2=-t 2+3 t+3=
[3+(-t 2+3 t)]×2=-t 2+3 t+3=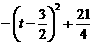
其中(0<t<3),由a=-1,0<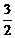 <3,此时
<3,此时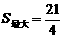 . …………(12分)
. …………(12分)
综上所述,当t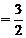 时,以点P,N,C,D为顶点的多边形面积有最大值,
时,以点P,N,C,D为顶点的多边形面积有最大值,
这个最大值为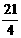 .
………………(13分)
.
………………(13分)
说明:(ⅱ)中的关系式,当t=0和t=3时也适合.
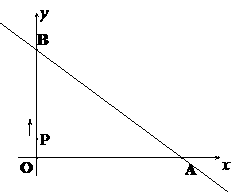
32.(09年黑龙江大兴安岭地区)28.(本小题满分10分)直线 与坐标轴分别交于
与坐标轴分别交于 、
、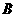 两点,
两点, 、
、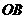 的长分别是方程
的长分别是方程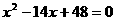 的两根(
的两根( ),动点
),动点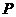 从
从 点出发,沿路线
点出发,沿路线 →
→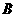 →
→ 以每秒1个单位长度的速度运动,到达
以每秒1个单位长度的速度运动,到达 点时运动停止.
点时运动停止.
(1)直接写出 、
、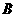 两点的坐标;
两点的坐标;
(2)设点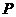 的运动时间为
的运动时间为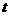 (秒),
(秒), 的面积为
的面积为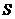 ,求
,求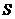 与
与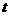 之间的函数关系式(不必写出自变量的取值范围);
之间的函数关系式(不必写出自变量的取值范围);
 (3)当
(3)当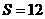 时,直接写出点
时,直接写出点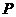 的坐标,此时,在坐标轴上是否存在点
的坐标,此时,在坐标轴上是否存在点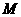 ,使以
,使以 、
、 、
、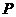 、
、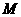 为顶点的四边形是梯形?若存在,请直接写出点
为顶点的四边形是梯形?若存在,请直接写出点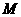 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(09年黑龙江大兴安岭地区28题解析)(1) 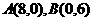 ……………………….各1分
……………………….各1分
(2)∵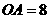 ,
,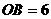 ,∴
,∴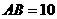
当点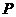 在
在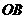 上运动时,
上运动时,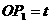 ,
,
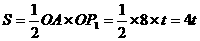 ;..............1分
;..............1分
当点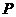 在
在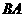 上运动时,作
上运动时,作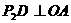 于点
于点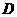 ,
,
有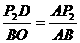
∵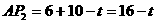 ,∴
,∴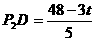 ………………………1分
………………………1分
∴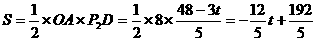 ……………………1分
……………………1分
(3)当 时,
时,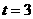 ,
, ,………………………………1分
,………………………………1分
此时,过 各顶点作对边的平行线,与坐标轴无第二个交点,所以点
各顶点作对边的平行线,与坐标轴无第二个交点,所以点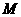 不存在;……………………………………………………………………………1分
不存在;……………………………………………………………………………1分
当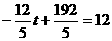 时,
时,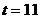 ,
,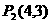 ,……………………1分
,……………………1分
此时,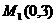 、
、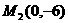 ………………………………………各1分
………………………………………各1分
注: 本卷中各题, 若有其它正确的解法,可酌情给分.
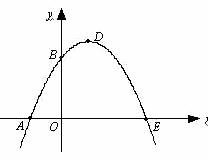
31.(09年贵州安顺)27、(本题满分12分)
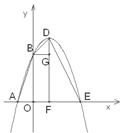
如图,已知抛物线与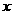 交于A(-1,0)、E(3,0)两点,与
交于A(-1,0)、E(3,0)两点,与 轴交于点B(0,3)。
轴交于点B(0,3)。
(1) 求抛物线的解析式;
(2) 设抛物线顶点为D,求四边形AEDB的面积;
(3) △AOB与△DBE是否相似?如果相似,请给以证明;如果不相似,请说明理由。
(09年贵州安顺27题解析)解:(1)(5′) ∵抛物线与 轴交于点(0,3),
轴交于点(0,3),
∴设抛物线解析式为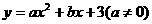 (1′)
(1′)
 根据题意,得
根据题意,得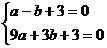 ,解得
,解得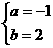
∴抛物线的解析式为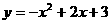 (5′)
(5′)
(2)(5′)由顶点坐标公式得顶点坐标为(1,4) (2′)
设对称轴与x轴的交点为F
∴四边形ABDE的面积=
=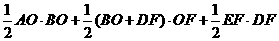
=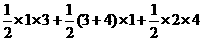 =9 (5′)
=9 (5′)
(3)(2′)相似
如图,BD=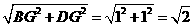 ;∴BE=
;∴BE=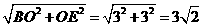
DE=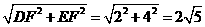 ∴
∴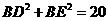 ,
, 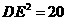
即: 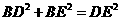 ,所以
,所以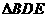 是直角三角形
是直角三角形
∴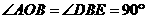 ,且
,且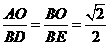 ,
,
∴ ∽
∽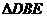 (2′)
(2′)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com