
题目列表(包括答案和解析)
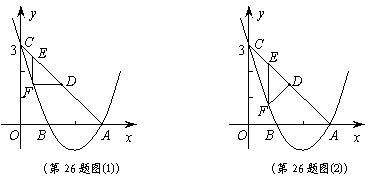
2.(09年福建龙岩)26.(14分)如图,抛物线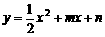 与x轴交于A、B两点,与y轴交于C点,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,2),连结BC、AD.
与x轴交于A、B两点,与y轴交于C点,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,2),连结BC、AD.
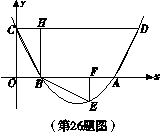 (1)求C点的坐标及抛物线的解析式;
(1)求C点的坐标及抛物线的解析式;
(2)将△BCH绕点B按顺时针旋转90°后 再沿x轴对折得到
△BEF(点C与点E对应),判断点E是否落在抛物线上,并说明理由;
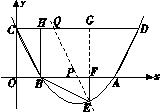
(3)设过点E的直线交AB边于点P,交CD边于点Q. 问是否存在点P,使直线PQ分梯形ABCD的面积为1∶3两部分?若存在,求出P点坐标;若不存在,请说明理由.
(09年福建龙岩26题解析)解:(1)∵四边形OBHC为矩形,∴CD∥AB,
 又D(5,2),
又D(5,2),
∴C(0,2),OC=2 . …………………………… 2分
∴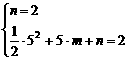 解得
解得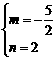
∴抛物线的解析式为: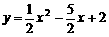 …… 4分
…… 4分
(2)点E落在抛物线上. 理由如下:……… 5分
由y = 0,得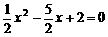 .
.
解得x1=1,x2=4. ∴A(4,0),B(1,0). ……………………………… 6分
∴OA=4,OB=1.
由矩形性质知:CH=OB=1,BH=OC=2,∠BHC=90°,
由旋转、轴对称性质知:EF=1,BF=2,∠EFB=90°,
∴点E的坐标为(3,-1). ………………………………………………… 7分
把x=3代入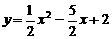 ,得
,得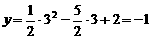 ,
,
∴点E在抛物线上. …………………………………………………………… 8分
(3)法一:存在点P(a,0),延长EF交CD于点G,易求OF=CG=3,PB=a-1.
S梯形BCGF = 5,S梯形ADGF = 3,记S梯形BCQP = S1,S梯形ADQP = S2,
下面分两种情形:
①当S1∶S2 =1∶3时,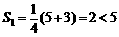 ,
,
此时点P在点F(3,0)的左侧,则PF = 3-a,
由△EPF∽△EQG,得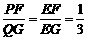 ,则QG=9-3a,
,则QG=9-3a,
∴CQ=3-(9-3a) =3a -6
由S1=2,得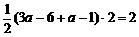 ,解得
,解得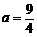 ;………………… 11分
;………………… 11分
②当S1∶S2=3∶1时,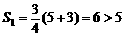
此时点P在点F(3,0)的右侧,则PF = a-3,
由△EPF∽△EQG,得QG = 3a-9,∴CQ = 3 +(3 a-9)= 3 a-6,
由S1=
6,得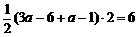 ,解得
,解得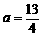 .
.
综上所述:所求点P的坐标为(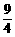 ,0)或(
,0)或(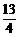 ,0)……… 14分
,0)……… 14分
法二:存在点P(a,0). 记S梯形BCQP = S1,S梯形ADQP = S2,易求S梯形ABCD = 8.
当PQ经过点F(3,0)时,易求S1=5,S2 = 3,
此时S1∶S2不符合条件,故a≠3.
设直线PQ的解析式为y = kx+b(k≠0),则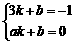 ,解得
,解得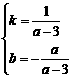 ,
,
∴ . 由y = 2得x = 3a-6,∴Q(3a-6,2) ……… 10分
. 由y = 2得x = 3a-6,∴Q(3a-6,2) ……… 10分
∴CQ = 3a-6,BP = a-1,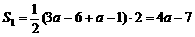 .
.
下面分两种情形:
①当S1∶S2 = 1∶3时, = 2;
= 2;
∴4a-7 = 2,解得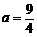 ;……………………………………………… 12分
;……………………………………………… 12分
②当S1∶S2 = 3∶1时,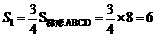 ;
;
∴4a-7 = 6,解得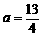 ;
;
综上所述:所求点P的坐标为(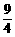 ,0)或(
,0)或(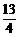 ,0)………… 14分
,0)………… 14分
[说明:对于第(3)小题,只要考生能求出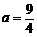 或
或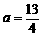 两个答案,就给6分. ]
两个答案,就给6分. ]
1.(09年安徽)23.已知某种水果的批发单价与批发量的函数关系如图(1)所示.
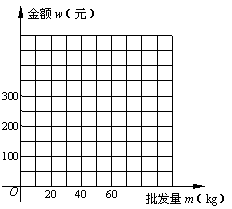 (1)请说明图中①、②两段函数图象的实际意义.
(1)请说明图中①、②两段函数图象的实际意义.
[解]

 (2)写出批发该种水果的资金金额w(元)与批发量m(kg)之间的
(2)写出批发该种水果的资金金额w(元)与批发量m(kg)之间的
函数关系式;在下图的坐标系中画出该函数图象;指出金额在什
么范围内,以同样的资金可以批发到较多数量的该种水果.
[解]
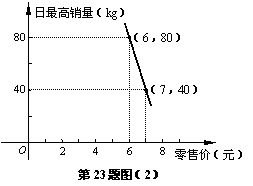
(3)经调查,某经销商销售该种水果的日最高销量与零售价之间的函
数关系如图(2)所示,该经销商拟每日售出60kg以上该种水果,
且当日零售价不变,请你帮助该经销商设计进货和销售的方案,
使得当日获得的利润最大.
[解]
(09年安徽23题解析)(1)解:图①表示批发量不少于20kg且不多于60kg的该种水果,
可按5元/kg批发;……3分
图②表示批发量高于60kg的该种水果,可按4元/kg批发.
………………………………………………………………3分
(2)解:由题意得: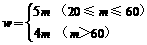 ,函数图象如图所示.
,函数图象如图所示.
………………………………………………………………7分
由图可知资金金额满足240<w≤300时,以同样的资金可
批发到较多数量的该种水果.……………………………8分
(3)解法一:
设当日零售价为x元,由图可得日最高销量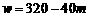
当m>60时,x<6.5
由题意,销售利润为
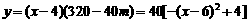 ………………………………12分
………………………………12分
当x=6时, ,此时m=80
,此时m=80
即经销商应批发80kg该种水果,日零售价定为6元/kg,
当日可获得最大利润160元.……………………………………………14分
解法二:
设日最高销售量为xkg(x>60)
则由图②日零售价p满足: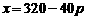 ,于是
,于是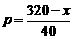
销售利润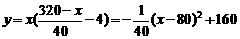 ………………………12分
………………………12分
当x=80时, ,此时p=6
,此时p=6
即经销商应批发80kg该种水果,日零售价定为6元/kg,
当日可获得最大利润160元.……………………………………………14分
24.(09年广西河池)26. (本小题满分12分)
如图12,已知抛物线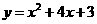 交
交 轴于A、B两点,交
轴于A、B两点,交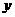 轴于点C,抛物线的对称轴交
轴于点C,抛物线的对称轴交 轴于点E,点B的坐标为(
轴于点E,点B的坐标为(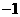 ,0).
,0).
(1)求抛物线的对称轴及点A的坐标;
(2)在平面直角坐标系 中是否存在点P,与A、B、C三点构成一个平行四边形?若存在,请写出点P的坐标;若不存在,请说明理由;
中是否存在点P,与A、B、C三点构成一个平行四边形?若存在,请写出点P的坐标;若不存在,请说明理由;
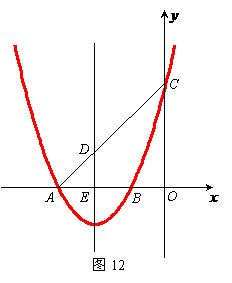 (3)连结CA与抛物线的对称轴交于点D,在抛物线上是否存在点M,使得直线CM把四边形DEOC分成面积相等的两部分?若存在,请求出直线CM的解析式;若不存在,请说明理由.
(3)连结CA与抛物线的对称轴交于点D,在抛物线上是否存在点M,使得直线CM把四边形DEOC分成面积相等的两部分?若存在,请求出直线CM的解析式;若不存在,请说明理由.
(09年广西河池25题解析)(1)① 对称轴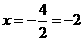 ···································· (2分)
···································· (2分)
② 当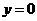 时,有
时,有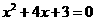
解之,得 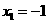 ,
,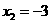
∴ 点A的坐标为(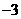 ,0).·································································· (4分)
,0).·································································· (4分)
(2)满足条件的点P有3个,分别为(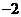 ,3),(2,3),(
,3),(2,3),(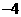 ,
,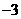 ).······· (7分)
).······· (7分)
(3)存在.··········································································································· (8分)
当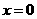 时,
时,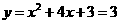 ∴ 点C的坐标为(0,3)
∴ 点C的坐标为(0,3)
∵ DE∥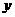 轴,AO
轴,AO 3,EO
3,EO 2,AE
2,AE 1,CO
1,CO 3
3
∴  ∽
∽ ∴
∴ 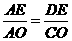 即
即 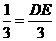 ∴ DE
∴ DE 1············· (9分)
1············· (9分)
∴ 
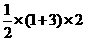
 4
4
在OE上找点F,使OF
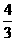 ,此时
,此时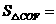

 2,直线CF把四边形DEOC
2,直线CF把四边形DEOC
分成面积相等的两部分,交抛物线于点M.························································ (10分)
设直线CM的解析式为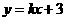 ,它经过点
,它经过点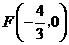 .
.
则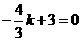 ·························································································· (11分)
·························································································· (11分)
解之,得 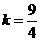 ∴ 直线CM的解析式为
∴ 直线CM的解析式为 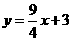 ·························· (12分)
·························· (12分)
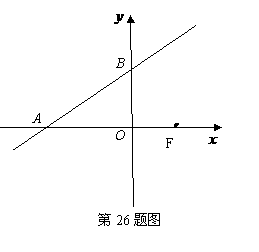
23.(09年广西桂林)26.(本题满分12分)如图,已知直线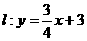 ,它与
,它与 轴、
轴、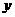 轴的交点
轴的交点
分别为A、B两点.
(1)求点A、点B的坐标;
(2)设F是 轴上一动点,用尺规作图作出⊙P,使⊙P经过点B且与
轴上一动点,用尺规作图作出⊙P,使⊙P经过点B且与 轴相切于点F(不写作法和证明,保留作图痕迹);
轴相切于点F(不写作法和证明,保留作图痕迹);
(3)设(2)中所作的⊙P的圆心坐标为P(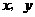 ),求
),求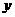 与
与 的函数关系式;
的函数关系式;
 (4)是否存在这样的⊙P,既与
(4)是否存在这样的⊙P,既与 轴相切又与直线
轴相切又与直线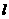 相切于点B,若存在,求出圆心P的坐标;若不存在,请说明理由.
相切于点B,若存在,求出圆心P的坐标;若不存在,请说明理由.
(09年广西桂林26题解析)解(1)A(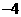 ,0),B(0,3)····· 2分(每对一个给1分)
,0),B(0,3)····· 2分(每对一个给1分)
(2)满分3分.其中过F作出垂线1分,作出BF中垂线1分,找出圆心并画出⊙P给1分.
(注:画垂线PF不用尺规作图的不扣分)
(3)过点P作PD⊥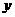 轴于D,则PD=
轴于D,则PD=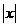 ,BD=
,BD=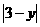 ,·········· 6分
,·········· 6分
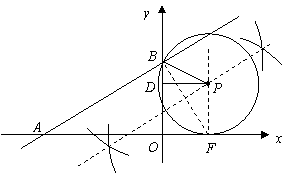 PB=PF=
PB=PF=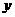 ,∵△BDP为直角三形,
,∵△BDP为直角三形,
∴
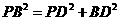
∴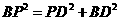 ···························· 7分
···························· 7分
即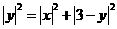
即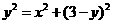
∴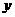 与
与 的函数关系为
的函数关系为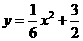 ·········································································· 8分
·········································································· 8分
(4)存在
解法1:∵⊙P与 轴相切于点F,且与直线
轴相切于点F,且与直线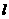 相切于点B
相切于点B
∴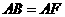 ················································································································ 9分
················································································································ 9分
∵
∴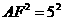
∵AF=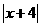 , ∴
, ∴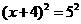 ··········································································· 10分
··········································································· 10分
∴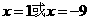 ········································································································ 11分
········································································································ 11分
把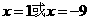 代入
代入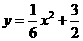 ,得
,得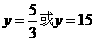
∴点P的坐标为(1,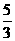 )或(
)或( 9,15)····································································· 12分
9,15)····································································· 12分
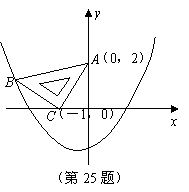
22.(09年广西崇左)25.(本小题满分16分)
在平面直角坐标系中,现将一块等腰直角三角板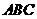 放在第二象限,斜靠在两坐标轴上,且点
放在第二象限,斜靠在两坐标轴上,且点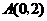 ,点
,点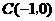 ,如图所示:抛物线
,如图所示:抛物线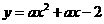 经过点
经过点 .
.
(1)求点 的坐标;
的坐标;
(2)求抛物线的解析式;
 (3)在抛物线上是否还存在点
(3)在抛物线上是否还存在点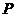 (点
(点 除外),使
除外),使 仍然是以
仍然是以 为直角边的等腰直角三角形?若存在,求所有点
为直角边的等腰直角三角形?若存在,求所有点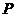 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 (09年广西崇左25题解析)(1)过点
(09年广西崇左25题解析)(1)过点 作
作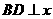 轴,垂足为
轴,垂足为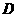 ,
,
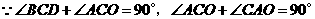
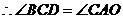 ;················································· 1分
;················································· 1分
又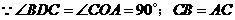 ,
,
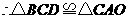 ,··············································· 2分
,··············································· 2分
 ·································· 3分
·································· 3分
 点
点 的坐标为
的坐标为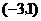 ;············································ 4分
;············································ 4分
(2)抛物线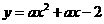 经过点
经过点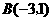 ,则得到
,则得到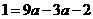 ,························ 5分
,························ 5分
解得 ,所以抛物线的解析式为
,所以抛物线的解析式为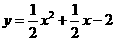 ;············································· 7分
;············································· 7分
(3)假设存在点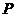 ,使得
,使得 仍然是以
仍然是以 为直角边的等腰直角三角形:
为直角边的等腰直角三角形:
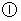 若以点
若以点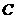 为直角顶点;
为直角顶点;
则延长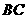 至点
至点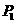 ,使得
,使得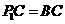 ,得到等腰直角三角形
,得到等腰直角三角形 ,··························· 8分
,··························· 8分
过点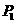 作
作 轴,
轴,
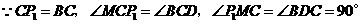 ;
;
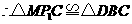 ·································································································· 10分
·································································································· 10分
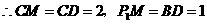 ,可求得点
,可求得点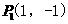 ;·········································· 11分
;·········································· 11分
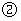 若以点
若以点 为直角顶点;
为直角顶点;
则过点 作
作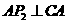 ,且使得
,且使得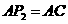 ,得到等腰直角三角形
,得到等腰直角三角形 ,·············· 12分
,·············· 12分
过点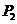 作
作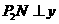 轴,同理可证
轴,同理可证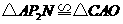 ;··············································· 13分
;··············································· 13分
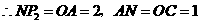 ,可求得点
,可求得点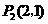 ;················································ 14分
;················································ 14分
经检验,点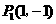 与点
与点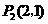 都在抛物线
都在抛物线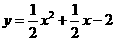 上.···························· 16分
上.···························· 16分
21.(09年广西来宾)26.(本小题满分12分)
当x=2时,抛物线y=ax2+bx+c取得最小值-1,并且抛物线与y轴交于点C(0,3),与x轴交于点A、B.
(1)求该抛物线的关系式;
(2)若点M(x,y1),N(x+1,y2)都在该抛物线上,试比较y1与y2的大小;
 (3)D是线段AC的中点,E为线段AC上一动点(A、C两端点除外),过点E作y轴的平行线EF与抛物线交于点F.问:是否存在△DEF与△AOC相似?若存在,求出点E的坐标;若不存在,则说明理由.
(3)D是线段AC的中点,E为线段AC上一动点(A、C两端点除外),过点E作y轴的平行线EF与抛物线交于点F.问:是否存在△DEF与△AOC相似?若存在,求出点E的坐标;若不存在,则说明理由.
(09年广西来宾26题解析)解:(1)由题意可设抛物线的关系式为y=a(x-2)2-1 …………1分
因为点C(0,3)在抛物线上
所以3=a(0-2)2-1,即a=1 …………………………2分
所以,抛物线的关系式为y=(x-2)2-1=x2-4 x+3 ……3分
(2)∵点M(x,y1),N(x+1,y2)都在该抛物线上
∴y1-y2=(x2-4 x+3)-[(x+1)2-4(x+1)+3]=3-2 x …………4分
当3-2 x>0,即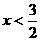 时,y1>y2 ………………………………5分
时,y1>y2 ………………………………5分
当3-2 x=0,即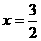 时,y1=y2 ………………………………6分
时,y1=y2 ………………………………6分
当3-2 x<0,即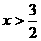 时,y1<y2 ………………………………7分
时,y1<y2 ………………………………7分
(3)令y=0,即x2-4 x+3=0,得点A(3,0),B(1,0),线段AC的中点为D(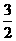 ,
,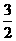 )
)
直线AC的函数关系式为y=-x+3 ………………………………8分
因为△OAC是等腰直角三角形,所以,要使△DEF与△OAC相似,△DEF也必须是等腰直角三角形.由于EF∥OC,因此∠DEF=45°,所以,在△DEF中只可能以点D、F为直角顶点.
①当F为直角顶点时,DF⊥EF,此时△DEF∽△ACO,DF所在直线为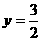
由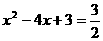 ,解得
,解得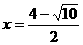 ,
, (舍去) ……9分
(舍去) ……9分
将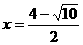 代入y=-x+3,得点E(
代入y=-x+3,得点E(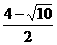 ,
,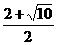 ) …………10分
) …………10分
②当D为直角顶点时,DF⊥AC,此时△DEF∽△OAC,由于点D为线段AC的中点,因此,DF所在直线过原点O,其关系式为y=x.
解x2-4 x+3=x,得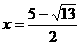 ,
,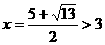 (舍去) …………11分
(舍去) …………11分
将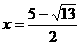 代入y=-x+3,得点E(
代入y=-x+3,得点E(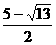 ,
,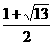 ) …………12分
) …………12分

20.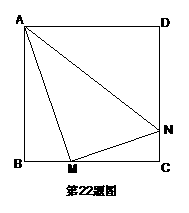 (09年广东)22. 正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,
(09年广东)22. 正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,
(1)证明:Rt△ABM ∽Rt△MCN;
(2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式;当M点运动到什么位置时,四边形ABCN的面积最大,并求出最大面积;
(3)当M点运动到什么位置时Rt△ABM ∽Rt△AMN,
求此时x的值.
(09年广东22题解析)(1)证明:∵四边形ABCD是正方形,∴∠B=∠C=90°,∠ABM+∠BAM=90°
∵∠ABM+∠CMN+∠AMN=180°,∠AMN=90°∴∠AMB+∠CMN=90°∴∠BAM=∠CMN
∴Rt△ABM∽Rt△MCN
(2)∵Rt△ABM∽Rt△MCN,∴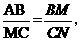 即
即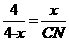 解得:
解得: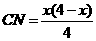
∵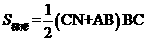 ∴
∴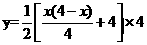 ,
,
即:
又∵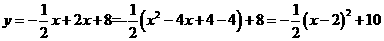
∴当x=2时,y有最大值10.
∴当M点运动到BC的中点时,四边形ABCN的面积最大,最大面积是10.
(3)∵Rt△ABM∽Rt△MCN,∴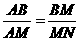 ,即
,即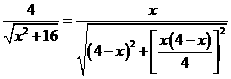
化简得: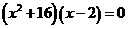 ,解得:x=2
,解得:x=2
∴当M点运动到BC的中点时Rt△ABM ∽Rt△AMN,此时x的值为2.
19.(09年广东肇庆)25.(本小题满分 10 分)
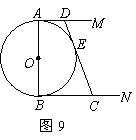
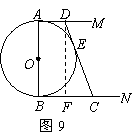
如图 9, 的直径
的直径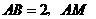 和
和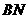 是它的两条切线,
是它的两条切线,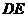 切
切 于E,交AM于D,
于E,交AM于D,
交BN 于C.设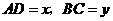 .
.
(1)求证: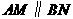 ;
;
(2)求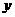 关于
关于 的关系式;
的关系式;
(3)求四边形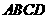 的面积S,并证明:
的面积S,并证明: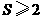 .
.
(09年广东肇庆25题解析)(1)证明:∵AB是直径,AM、BN是切线,
 ∴
∴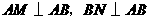 ,∴
,∴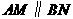 .················· (2 分)
.················· (2 分)
解:(2)过点D作 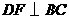 于F,则
于F,则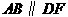 .
.
由(1)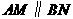 ,∴四边形
,∴四边形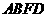 为矩形.
为矩形.
∴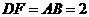 ,
,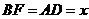 .································ (3 分)
.································ (3 分)
∵DE、DA,CE、CB都是切线,
∴根据切线长定理,得
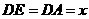 ,
,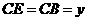 .··································· (4 分)
.··································· (4 分)
在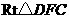 中,
中,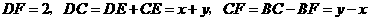 ,
,
∴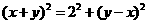 ,················································································· (5 分)
,················································································· (5 分)
化简,得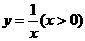 .······················································································· (6分)
.······················································································· (6分)
(3)由(1)、(2)得,四边形的面积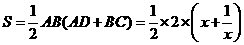 ,
,
即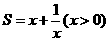 .···························································································· (8分)
.···························································································· (8分)
∵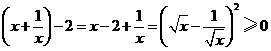 ,当且仅当
,当且仅当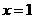 时,等号成立.
时,等号成立.
∴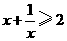 ,即
,即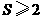 .··················································································· (10分)
.··················································································· (10分)
18.(09年广东湛江)28.已知矩形纸片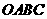 的长为4,宽为3,以长
的长为4,宽为3,以长 所在的直线为
所在的直线为 轴,
轴, 为坐标原点建
为坐标原点建
立平面直角坐标系;点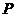 是
是 边上的动点(与点
边上的动点(与点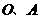 不重合),现将
不重合),现将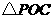 沿
沿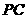 翻折
翻折
得到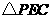 ,再在
,再在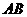 边上选取适当的点
边上选取适当的点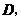 将
将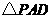 沿
沿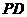 翻折,得到
翻折,得到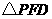 ,使得
,使得
直线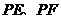 重合.
重合.
(1)若点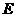 落在
落在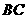 边上,如图①,求点
边上,如图①,求点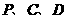 的坐标,并求过此三点的抛物线的函数关系式;
的坐标,并求过此三点的抛物线的函数关系式;
(2)若点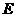 落在矩形纸片
落在矩形纸片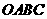 的内部,如图②,设
的内部,如图②,设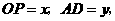 当
当 为何值时,
为何值时,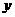 取得最大值?
取得最大值?
(3)在(1)的情况下,过点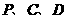 三点的抛物线上是否存在点
三点的抛物线上是否存在点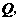 使
使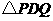 是以
是以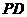 为直角边的直角三角形?若不存在,说明理由;若存在,求出点
为直角边的直角三角形?若不存在,说明理由;若存在,求出点 的坐标
的坐标
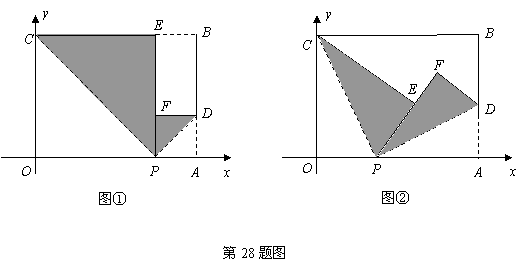
(09年广东湛江28题解析)解:(1)由题意知,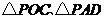 均为等腰直角三角形,
均为等腰直角三角形,
可得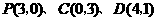 ······················································································· 2分
······················································································· 2分

设过此三点的抛物线为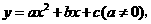 则
则
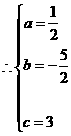
 过
过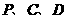 三点的抛物线的函数关系式为
三点的抛物线的函数关系式为 ··································· 4分
··································· 4分
(2)由已知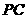 平分
平分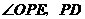 平分
平分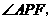 且
且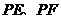 重合,则
重合,则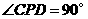
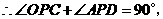 又
又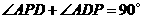
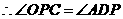 .
.
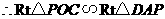 .
.
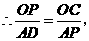 即
即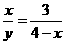 ······················································································· 6分
······················································································· 6分
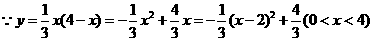
 当
当 时,
时,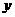 有最大值
有最大值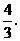 ··················································································· 8分
··················································································· 8分
(3)假设存在,分两种情况讨论:
①当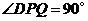 时,由题意可知
时,由题意可知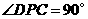 ,且点
,且点 在抛物线上,故点
在抛物线上,故点 与点
与点 重合,所求的点
重合,所求的点 为(0,3) 9分
为(0,3) 9分
②当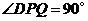 时,过点
时,过点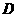 作平行于
作平行于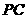 的直线
的直线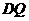 ,假设直线
,假设直线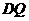 交抛物线于另一点
交抛物线于另一点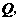
 点
点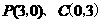 ,
, 直线
直线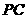 的方程为
的方程为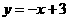 ,将直线
,将直线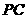 向上平移2个单位与直线
向上平移2个单位与直线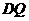 重合,
重合, 直线
直线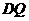 的方程为
的方程为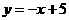 10分
10分
由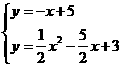 得
得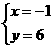 或
或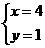
又点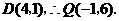
故该抛物线上存在两点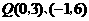 满足条件.························································· 12分
满足条件.························································· 12分

说明:以上各题如有其他解(证)法,请酌情给分.
17.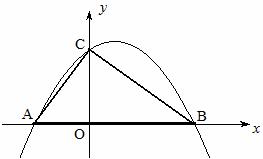 (09年广东深圳)23.(本题10分)已知:Rt△ABC的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与x轴重合(其中OA<OB),直角顶点C落在y轴正半轴上(如图11)。
(09年广东深圳)23.(本题10分)已知:Rt△ABC的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与x轴重合(其中OA<OB),直角顶点C落在y轴正半轴上(如图11)。
(1)求线段OA、OB的长和经过点A、B、C的抛物线的关系式。(4分)
(2)如图12,点D的坐标为(2,0),点P(m,n)是该抛物线上的一个动点(其中m>0,n>0),连接DP交BC于点E。
|
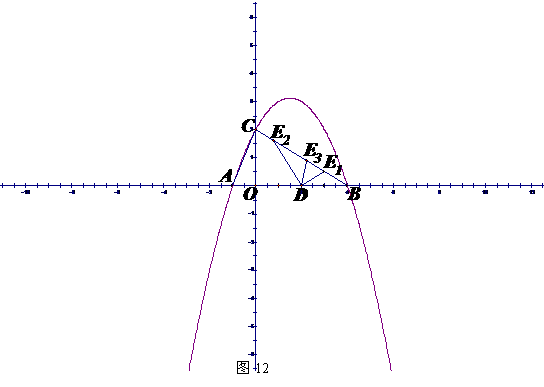 ②又连接CD、CP(如图13),△CDP是否有最大面积?若有,求出△CDP的最大面积和此时点P的坐标;若没有,请说明理由。(3分)
②又连接CD、CP(如图13),△CDP是否有最大面积?若有,求出△CDP的最大面积和此时点P的坐标;若没有,请说明理由。(3分)

(09年广东深圳23题解析)
(1) 由Rt△AOC∽Rt△COB易知,CO2=OA.OB=OA(AB-OA),可求OA=1,OB=4
∴A(-1,0) B(4,0) C(0,2)
可设解析式为y=a(x+1)(x-4),将点C(0,2)代入,可求a=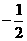
∴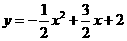 为所求
为所求
(2)
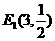 ;
;
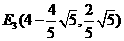 提示:直线BC的解析式为
提示:直线BC的解析式为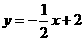 设
设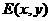 ,利用勾股定理和点
,利用勾股定理和点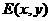 在直线BC上,可得两个方程组
在直线BC上,可得两个方程组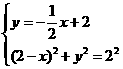
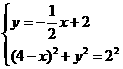 分别可求
分别可求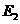 和
和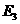
(3)
过D作X轴的垂线,交PC于M,易求PC的解析式为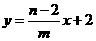 ,且
,且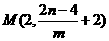 ,故
,故
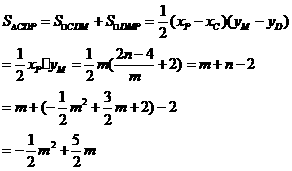
故,当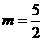 时,
时,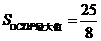 ,
,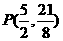
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com