
题目列表(包括答案和解析)
11.(09年广东佛山)25.一般地,学习几何要从作图开始,再观察图形,根据图形的某一类共同特征对图形进行分类(即给一类图形下定义--定义概念便于归类、交流与表达),然后继续研究图形的其它特征、判定方法以及图形的组合、图形之间的关系、图形的计算等问题. 课本里对四边形的研究即遵循着上面的思路.
当然,在学习几何的不同阶段,可能研究的是几何的部分问题.比如有下面的问题,请你研究.
已知:四边形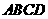 中,
中,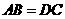 ,且
,且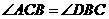 .
.
(1)借助网格画出四边形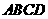 所有可能的形状;
所有可能的形状;

(2)简要说明在什么情况下四边形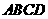 具有所画的形状.
具有所画的形状.
(09年广东佛山25题解析)(1)四边形可能的形状有三类:图 “矩形”、图
“矩形”、图 “等腰梯形”、图
“等腰梯形”、图 的“四边形
的“四边形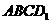 ”.
”.
注1:画出“矩形”或“等腰梯形”,各给1分;画出另一类图形(后两种可以看作一类),给2分;
等腰梯形不单独画而在后两种图中反映的,不扣分;画图顺序不同但答案正确不扣分.

注2:如果在类似图 或图④的图中画出凹四边形,同样给分(两种都画,只给一种的分).
或图④的图中画出凹四边形,同样给分(两种都画,只给一种的分).
(2) (i)若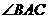 是直角(图
是直角(图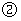 ),则四边形为等腰梯形;······································ 6分
),则四边形为等腰梯形;······································ 6分
(ii)若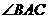 是锐角(图
是锐角(图 ),存在两个点
),存在两个点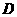 和
和 ,得到等腰梯形
,得到等腰梯形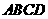 和符合条件但不是梯形的四边形
和符合条件但不是梯形的四边形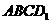 ;······································································································································ 8分
;······································································································································ 8分
其中,若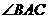 是直角(图
是直角(图 ),则四边形为矩形.················································
9分
),则四边形为矩形.················································
9分
(iii)若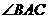 是钝角(图④),存在两个点
是钝角(图④),存在两个点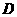 和
和 ,得到等腰梯形
,得到等腰梯形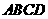 和符合条件但不是梯形的四边形
和符合条件但不是梯形的四边形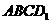 ;··································································································································
11分
;··································································································································
11分
注:可用 与
与 或者
或者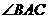 与
与 是否相等分类;只画矩形和等腰梯形并进行说明可给4分.
是否相等分类;只画矩形和等腰梯形并进行说明可给4分.
10.(09年甘肃庆阳)29.(12分)如图18,在平面直角坐标系中,将一块腰长为5的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(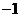 ,0),点B在抛物线
,0),点B在抛物线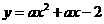 上.
上.
(1)点A的坐标为 ,点B的坐标为 ;
(2)抛物线的关系式为 ;
(3)设(2)中抛物线的顶点为D,求△DBC的面积;
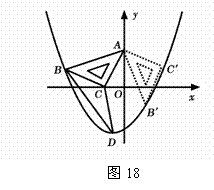 (4)将三角板ABC绕顶点A逆时针方向旋转90°,到达
(4)将三角板ABC绕顶点A逆时针方向旋转90°,到达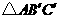 的位置.请判断点
的位置.请判断点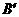 、
、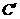 是否在(2)中的抛物线上,并说明理由.
是否在(2)中的抛物线上,并说明理由.
(09年甘肃庆阳29题解析)解: (1)A(0,2), B(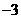 ,1).···························· 2分
,1).···························· 2分
(2)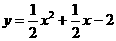 .······················································································· 3分
.······················································································· 3分
(3)如图1,可求得抛物线的顶点D(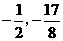 ).············································· 4分
).············································· 4分
设直线BD的关系式为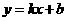 , 将点B、D的坐标代入,求得
, 将点B、D的坐标代入,求得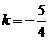 ,
,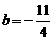 ,
,
∴ BD的关系式为 .········································································ 5分
.········································································ 5分
设直线BD和x 轴交点为E,则点E(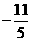 ,0),CE=
,0),CE=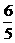 .
.
∴ △DBC的面积为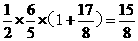 .························································ 7分
.························································ 7分
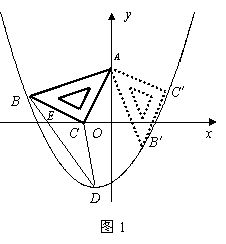
(4)如图2,过点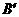 作
作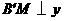 轴于点M,过点B作
轴于点M,过点B作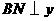 轴于点N,过点
轴于点N,过点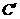 作
作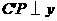 轴于点P. 8分
轴于点P. 8分

在Rt△AB′M与Rt△BAN中,
∵ AB=AB′, ∠AB′M=∠BAN=90°-∠B′AM,
∴ Rt△AB′M≌Rt△BAN.····················································································· 9分
∴ B′M=AN=1,AM=BN=3, ∴ B′(1,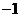 ).··················································· 10分
).··················································· 10分
同理△AC′P≌△CAO,C′P=OA=2,AP=OC=1,可得点C′(2,1);····················· 11分
将点B′、C′的坐标代入 ,可知点B′、C′在抛物线上.················ 12分
,可知点B′、C′在抛物线上.················ 12分
(事实上,点P与点N重合)
9.(09年甘肃兰州)29.(本题满分9分)如图①,正方形 ABCD中,点A、B的坐标分别为(0,10),(8,4),
点C在第一象限.动点P在正方形 ABCD的边上,从点A出发沿A→B→C→D匀速运动,
同时动点Q以相同速度在x轴正半轴上运动,当P点到达D点时,两点同时停止运动,
设运动的时间为t秒.
(1)当P点在边AB上运动时,点Q的横坐标 (长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;
(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;
(2)求正方形边长及顶点C的坐标;
(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标;
(4)如果点P、Q保持原速度不变,当点P沿A→B→C→D匀速运动时,OP与PQ能否相等,若能,写出所有符合条件的t的值;若不能,请说明理由.

(09年甘肃兰州29题解析)解:(1)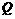 (1,0)······················································· 1分
(1,0)······················································· 1分
点P运动速度每秒钟1个单位长度.··········································································· 2分
(2) 过点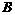 作BF⊥y轴于点
作BF⊥y轴于点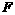 ,
,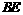 ⊥
⊥ 轴于点
轴于点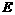 ,则
,则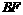 =8,
=8, .
.
 ∴
∴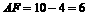 .
.
在Rt△AFB中,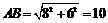 3分
3分
过点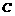 作
作 ⊥
⊥ 轴于点
轴于点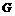 ,与
,与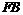 的延长线交于点
的延长线交于点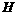 .
.
∵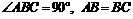 ∴△ABF≌△BCH.
∴△ABF≌△BCH.
∴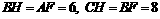 .
.
∴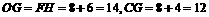 .
.
∴所求C点的坐标为(14,12). 4分
(3) 过点P作PM⊥y轴于点M,PN⊥ 轴于点N,
轴于点N,
则△APM∽△ABF.
∴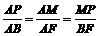 .
.
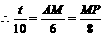 .
.
∴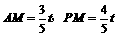 .
∴
.
∴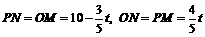 .
.
设△OPQ的面积为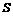 (平方单位)
(平方单位)
∴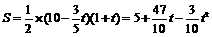 (0≤
(0≤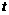 ≤10) ························································ 5分
≤10) ························································ 5分
说明:未注明自变量的取值范围不扣分.
∵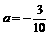 <0 ∴当
<0 ∴当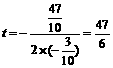 时, △OPQ的面积最大.······························ 6分
时, △OPQ的面积最大.······························ 6分
此时P的坐标为(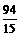 ,
,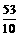 ) .················································································· 7分
) .················································································· 7分
(4) 当 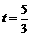 或
或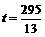 时,
OP与PQ相等.························································· 9分
时,
OP与PQ相等.························································· 9分
对一个加1分,不需写求解过程.
8.(09年甘肃定西)28.如图14(1),抛物线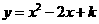 与x轴交于A、B两点,与y轴交于点C(0,
与x轴交于A、B两点,与y轴交于点C(0,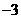 ).[图14(2)、图14(3)为解答备用图]
).[图14(2)、图14(3)为解答备用图]
(1)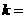 ,点A的坐标为 ,点B的坐标为 ;
,点A的坐标为 ,点B的坐标为 ;
(2)设抛物线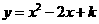 的顶点为M,求四边形ABMC的面积;
的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由;
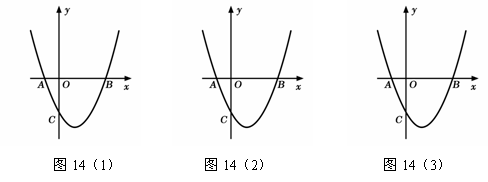 (4)在抛物线
(4)在抛物线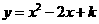 上求点Q,使△BCQ是以BC为直角边的直角三角形.
上求点Q,使△BCQ是以BC为直角边的直角三角形.
(09年甘肃定西28题解析)解:(1)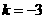 ,··················· 1分
,··················· 1分
A(-1,0),····························································· 2分
B(3,0).······························································· 3分
(2)如图14(1),抛物线的顶点为M(1,-4),连结OM.
······································································ 4分
则 △AOC的面积=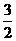 ,△MOC的面积=
,△MOC的面积=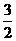 ,
,
△MOB的面积=6,····················································· 5分
∴ 四边形 ABMC的面积
=△AOC的面积+△MOC的面积+△MOB的面积=9.········································· 6分
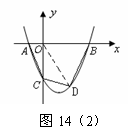 说明:也可过点M作抛物线的对称轴,将四边形ABMC的面
说明:也可过点M作抛物线的对称轴,将四边形ABMC的面
积转化为求1个梯形与2个直角三角形面积的和.
(3)如图14(2),设D(m,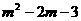 ),连结OD.
),连结OD.
则 0<m<3,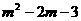 <0.
<0.
且 △AOC的面积=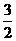 ,△DOC的面积=
,△DOC的面积=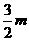 ,
,
△DOB的面积=-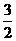 (
(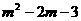 ),····························································· 8分
),····························································· 8分
∴ 四边形 ABDC的面积=△AOC的面积+△DOC的面积+△DOB的面积
=
=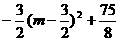 .···················································································· 9分
.···················································································· 9分
 ∴ 存在点D
∴ 存在点D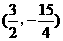 ,使四边形ABDC的面积最大为
,使四边形ABDC的面积最大为 .······························ 10分
.······························ 10分
(4)有两种情况:
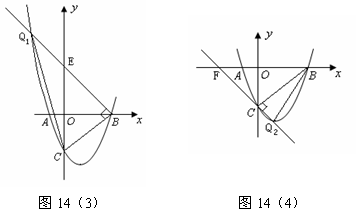
如图14(3),过点B作BQ1⊥BC,交抛物线于点Q1、交y轴于点E,连接Q1C.
∵ ∠CBO=45°,∴∠EBO=45°,BO=OE=3.
∴ 点E的坐标为(0,3).
∴ 直线BE的解析式为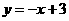 .···································································· 12分
.···································································· 12分
由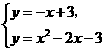 解得
解得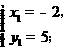
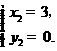
∴ 点Q1的坐标为(-2,5).··············································································· 13分
如图14(4),过点C作CF⊥CB,交抛物线于点Q2、交x轴于点F,连接BQ2.
∵ ∠CBO=45°,∴∠CFB=45°,OF=OC=3.
∴ 点F的坐标为(-3,0).
∴ 直线CF的解析式为 .···································································· 14分
.···································································· 14分
由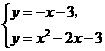 解得
解得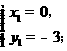
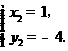
∴点Q2的坐标为(1,-4).················································································· 15分
综上,在抛物线上存在点Q1(-2,5)、Q2(1,-4),使△BCQ1、△BCQ2是以BC为直角边的直角三角形. 16分
说明:如图14(4),点Q2即抛物线顶点M,直接证明△BCM为直角三角形同样得2分.
7.(09年福建福州)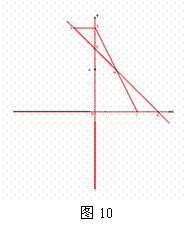 22.(满分14分)
22.(满分14分)
已知直线l:y=-x+m(m≠0)交x轴、y轴于A、B两点,点C、M分别在
线段OA、AB上,且OC=2CA,AM=2MB,连接MC,将△ACM绕点M
旋转180°,得到△FEM,则点E在y轴上, 点F在直线l上;取线段EO中
点N,将ACM沿MN所在直线翻折,得到△PMG,其中P与A为对称点.记:
过点F的双曲线为 ,过点M且以B为顶点的抛物线为
,过点M且以B为顶点的抛物线为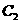 ,过点P且以M
,过点P且以M
为顶点的抛物线为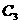 .
.
(1) 如图10,当m=6时,①直接写出点M、F的坐标,
②求 、
、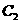 的函数解析式;
的函数解析式;
(2)当m发生变化时,
①在 的每一支上,y随x的增大如何变化?请说明理由。
的每一支上,y随x的增大如何变化?请说明理由。
②若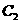 、
、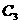 中的y都随着x的增大而减小,写出x的取值范围。
中的y都随着x的增大而减小,写出x的取值范围。
(09年福建福州22题解析)解:(1)①点M的坐标为(2,4),点F的坐标为(-2,8).……………………2分
②
设 的函数解析式为
的函数解析式为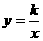 (
(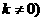 .
.
∵ 过点F(-2,8)
过点F(-2,8)
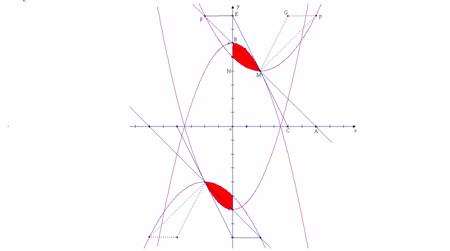
∴ 的函数解析式为
的函数解析式为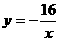 .
.
 ∵
∵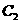 的顶点B的坐标是(0,6)
的顶点B的坐标是(0,6)
∴设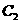 的函数解析式为
的函数解析式为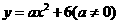 .
.
∵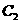 过点M(2,4)
过点M(2,4)
∴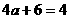
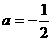 .
.
∴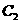 的函数解析式为
的函数解析式为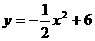 .……………………6分
.……………………6分
(2)依题意得,A(m,0),B(0,m),
∴点M坐标为(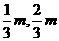 ),点F坐标为(
),点F坐标为(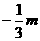 ,
,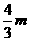 ).
).
①设 的函数解析式为
的函数解析式为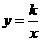 (
(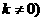 .
.
∵ 过点F(
过点F(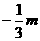 ,
,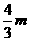 )
)
∴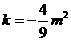 .
.
∵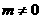
∴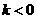
∴在 的每一支上,y随着x的增大而增大.
的每一支上,y随着x的增大而增大.
②答:当 >0时,满足题意的x的取值范围为 0<x<
>0时,满足题意的x的取值范围为 0<x<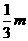 ;
;
当 <0时,满足题意的x的取值范围为
<0时,满足题意的x的取值范围为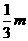 <x<0.………………………………14分
<x<0.………………………………14分
6.(09年福建厦门)26.(11分)已知二次函数y=x2-x+c.
(1)若点A(-1,a)、B(2,2n-1)在二次函数y=x2-x+c的图象上,求此二次函数的最小值;
(2)若点D(x1,y1)、E(x2,y2)、P(m,n)(m>n)在二次函数y=x2-x+c的图象上,且D、E两点关于坐标原点成中心对称,连接OP.当2≤OP≤2+时,试判断直线DE与抛物线y=x2-x+c+的交点个数,并说明理由.
(09年福建厦门26题解析) (1)解:法1:由题意得 ……1分
解得 ……2分
法2:∵ 抛物线y=x2-x+c的对称轴是x=,
且 -(-1) =2-,∴ A、B两点关于对称轴对称.
∴ n=2n-1 ……1分
∴ n=1,c=-1. ……2分
∴ 有 y=x2-x-1 ……3分
=(x-)2-.
∴ 二次函数y=x2-x-1的最小值是-. ……4分
(2)解:∵ 点P(m,m)(m>0),
∴ PO=m.
∴ 2≤m ≤+2.
∴ 2≤m≤1+. ……5分
法1: ∵ 点P(m,m)(m>0)在二次函数y=x2-x+c的图象上,
∴ m=m2-m+c,即c=-m2+2m.
∵ 开口向下,且对称轴m=1,
∴ 当2≤m≤1+ 时,
有 -1≤c≤0. ……6分
法2:∵ 2≤m≤1+,
∴ 1≤m-1≤.
∴ 1≤(m-1)2≤2.
∵ 点P(m,m)(m>0)在二次函数y=x2-x+c的图象上,
∴ m=m2-m+c,即1-c=(m-1)2.
∴ 1≤1-c≤2.
∴ -1≤c≤0. ……6分
∵ 点D、E关于原点成中心对称,
法1: ∴ x2=-x1,y2=-y1.
∴
∴ 2y1=-2x1, y1=-x1.
设直线DE:y=kx.
有 -x1=kx1.
由题意,存在x1≠x2.
∴ 存在x1,使x1≠0. ……7分
∴ k=-1.
∴ 直线DE: y=-x. ……8分
法2:设直线DE:y=kx.
则根据题意有 kx=x2-x+c,即x2-(k+1) x+c=0.
∵ -1≤c≤0,
∴ (k+1)2-4c≥0.
∴ 方程x2-(k+1) x+c=0有实数根. ……7分
∵ x1+x2=0,
∴ k+1=0.
∴ k=-1.
∴ 直线DE: y=-x. ……8分
若 则有 x2+c+=0.即 x2=-c-.
① 当 -c-=0时,即c=-时,方程x2=-c-有相同的实数根,
即直线y=-x与抛物线y=x2-x+c+有唯一交点. ……9分
② 当 -c->0时,即c<-时,即-1≤c<-时,
方程x2=-c-有两个不同实数根,
即直线y=-x与抛物线y=x2-x+c+有两个不同的交点. ……10分
③ 当 -c-<0时,即c>-时,即-<c≤0时,
方程x2=-c-没有实数根,
即直线y=-x与抛物线y=x2-x+c+没有交点. ……11分
3.6或12.……………………………………………………………(13分)
5.(09年福建泉州)28.(13分)在直角坐标系中,点A(5,0)关于原点O的对称点为点C.
(1)请直接写出点C的坐标;
(2)若点B在第一象限内,∠OAB=∠OBA,并且点B关于原点O的对称点为点D.
①试判断四边形ABCD的形状,并说明理由;
②现有一动点P从B点出发,沿路线BA-AD以每秒1个单位长的速度向终点D运动,另一动点Q从A点同时出发,沿AC方向以每秒0.4个单位长的速度向终点C运动,当其中一个动点到达终点时,另一个动点也随之停止运动.已知AB=6,设点P、Q的运动时间为t秒,在运动过程中,当动点Q在以PA为直径的圆上时,试求t的值.
(09年福建泉州28题解析)28.(本小题13分)
 解:(1)C(-5,0)…………………………………………(3分)
解:(1)C(-5,0)…………………………………………(3分)
(2)①四边形ABCD为矩形,理由如下:
如图,由已知可得:A、O、C在同一直线上,且 OA=OC;B、O、D在同一直线上,且OB=OD,∴四边形ABCD是平行四边形.…………………………………………………………(5分)
∵∠OAB=∠OBA∴OA=OB,即AC=2OA=2OB=BD
∴四边形ABCD是矩形.……………………………………(7分)
②如图,由①得四边形ABCD是矩形
∴∠CBA=∠ADC=90°………………………………………(8分)
又AB=CD=6,AC=10
∴由勾股定理,得BC=AD=
=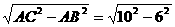 =8…………………………………(9分)
=8…………………………………(9分)
∵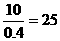 ,
,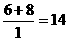 ,∴0≤t≤14.……………………(10分)
,∴0≤t≤14.……………………(10分)
当0≤t≤6时,P点在AB上,连结PQ.
∵AP是直径,∴∠PQA=90°…………………………………(11分)
又∠PAQ=∠CAB,∴△PAQ∽△CAB
∴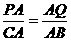 ,即
,即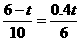 ,解得t=3.6…………………………(12分)
,解得t=3.6…………………………(12分)
当6<t≤14时,P点在AD上,连结PQ,
同理得∠PQA=90°,△PAQ∽△CAD
∴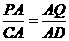 ,即
,即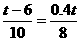 t-6,解得t=12.
t-6,解得t=12.
综上所述,当动点Q在以PA为直径的圆上时,t的值为
4.(09年福建莆田)25.(14分)已知,如图1,过点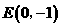 作平行于
作平行于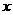 轴的直线
轴的直线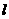 ,抛物线
,抛物线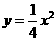 上的两点
上的两点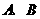 的横坐标分别为
的横坐标分别为 1和4,直线
1和4,直线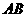 交
交 轴于点
轴于点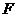 ,过点
,过点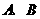 分别作直线
分别作直线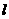 的垂线,垂足分别为点
的垂线,垂足分别为点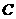 、
、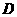 ,连接
,连接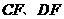 .
.
(1)求点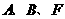 的坐标;
的坐标;
(2)求证: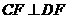 ;
;
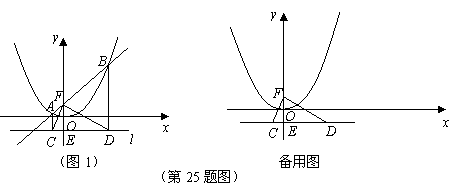 (3)点
(3)点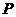 是抛物线
是抛物线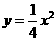 对称轴右侧图象上的一动点,过点
对称轴右侧图象上的一动点,过点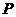 作
作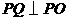 交
交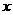 轴于点
轴于点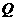 ,是否存在点
,是否存在点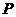 使得
使得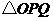 与
与 相似?若存在,请求出所有符合条件的点
相似?若存在,请求出所有符合条件的点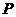 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(09年福建莆田25题解析)25.(1)解:方法一,如图1,当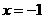 时,
时,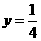
当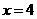 时,
时,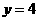
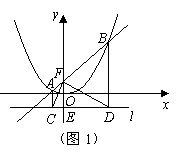 ∴
∴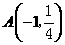 ·············································································· 1分
·············································································· 1分
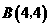 ······················································································ 2分
······················································································ 2分
设直线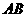 的解析式为
的解析式为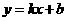 ··············································· 3分
··············································· 3分
则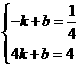 解得
解得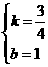
∴直线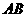 的解析式为
的解析式为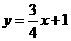 ·············································· 4分
·············································· 4分
当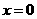 时,
时,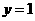

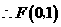 ···························································································································· 5分
···························································································································· 5分
方法二:求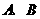 两点坐标同方法一,如图2,作
两点坐标同方法一,如图2,作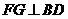 ,
,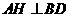 ,垂足分别为
,垂足分别为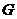 、
、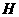 ,交
,交 轴于点
轴于点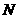 ,则四边形
,则四边形 和四边形
和四边形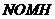 均为矩形,设
均为矩形,设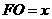 ························· 3分
························· 3分
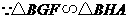
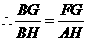
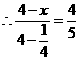 ······················································································································· 4分
······················································································································· 4分
解得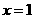
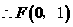 ························································································································· 5分
························································································································· 5分
(2)证明:方法一:在 中,
中,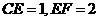
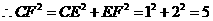
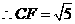 ························································································································ 6分
························································································································ 6分
在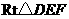 中,
中,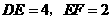
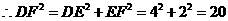
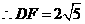
由(1)得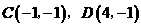
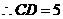
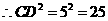
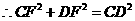 ··································································································· 7分
··································································································· 7分
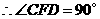

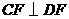 ················································································································ 8分
················································································································ 8分
方法二:由 (1)知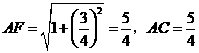
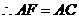 ················································································································· 6分
················································································································· 6分
同理: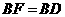
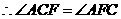
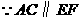

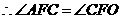 ······································································································· 7分
······································································································· 7分
同理: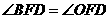
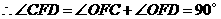
即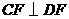 ················································································································ 8分
················································································································ 8分
(3)存在.
解:如图3,作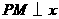 轴,垂足为点
轴,垂足为点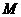 ··········· 9分
··········· 9分
 又
又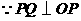
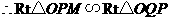

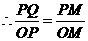 ···················································· 10分
···················································· 10分
设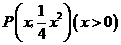 ,则
,则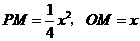
①当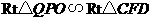 时,
时,
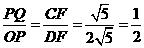 ································································································ 11分
································································································ 11分
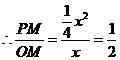
解得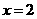
 ···················································································································· 12分
···················································································································· 12分
②当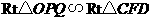 时,
时,
 ································································································ 13分
································································································ 13分
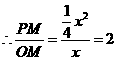
解得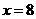
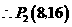
综上,存在点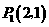 、
、 使得
使得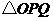 与
与 相似.··································· 14分
相似.··································· 14分
3.(09年福建宁德)26.(本题满分13分)如图,已知抛物线C1: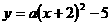 的顶点为P,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
的顶点为P,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
(1)求P点坐标及a的值;(4分)
(2)如图(1),抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移,平移后的抛物线记为C3,C3的顶点为M,当点P、M关于点B成中心对称时,求C3的解析式;(4分)
(3)如图(2),点Q是x轴正半轴上一点,将抛物线C1绕点Q旋转180°后得到抛物线C4.抛物线C4的顶点为N,与x轴相交于E、F两点(点E在点F的左边),当以点P、N、F为顶点的三角形是直角三角形时,求点Q的坐标.(5分)


(09年福建宁德26题解析)解:(1)由抛物线C1: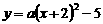 得
得
顶点P的为(-2,-5) ………2分
∵点B(1,0)在抛物线C1上
∴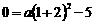
解得,a= ………4分
(2)连接PM,作PH⊥x轴于H,作MG⊥x轴于G
∵点P、M关于点B成中心对称
∴PM过点B,且PB=MB
∴△PBH≌△MBG
∴MG=PH=5,BG=BH=3
∴顶点M的坐标为(4,5) ………6分
抛物线C2由C1关于x轴对称得到,抛物线C3由C2平移得到
∴抛物线C3的表达式为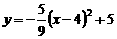 ………8分
………8分
(3)∵抛物线C4由C1绕点x轴上的点Q旋转180°得到
∴顶点N、P关于点Q成中心对称
由(2)得点N的纵坐标为5
 设点N坐标为(m,5)
………9分
设点N坐标为(m,5)
………9分
作PH⊥x轴于H,作NG⊥x轴于G
作PK⊥NG于K
∵旋转中心Q在x轴上
∴EF=AB=2BH=6
∴FG=3,点F坐标为(m+3,0)
H坐标为(2,0),K坐标为(m,-5),
根据勾股定理得
PN2=NK2+PK2=m2+4m+104
PF2=PH2+HF2=m2+10m+50
NF2=52+32=34 ………10分
①当∠PNF=90º时,PN2+ NF2=PF2,解得m=,∴Q点坐标为(,0)
②当∠PFN=90º时,PF2+ NF2=PN2,解得m=,∴Q点坐标为(,0)
③∵PN>NK=10>NF,∴∠NPF≠90º
综上所得,当Q点坐标为(,0)或(,0)时,以点P、N、F为顶点
的三角形是直角三角形. ………13分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com