
题目列表(包括答案和解析)
9. (2009南州)设矩形ABCD的长与宽的和为2,以AB为轴心旋转一周得到一个几何体,则此几何体的侧面积有( )
A、最小值4π B、最大值4π
C、最大值2π D、最小值2π
8. (2009泸州)已知⊙O1与⊙O2的半径分别为5cm和3cm,圆心距020=7cm,则两圆的位置关系为
A.外离 B.外切 C.相交 D.内切
7. (2009宜宾)若两圆的半径分别是2cm和3cm,圆心距为5cm,则这两圆的位置关系是( )
A.内切 B.相交 C.外切 D.外离
6.
(2009台州)如图,⊙ 的内接多边形周长为3 ,⊙
的内接多边形周长为3 ,⊙ 的外切多边形周长为3.4,
的外切多边形周长为3.4,
则下列各数中与此圆的周长最接近的是( ▲ )
A.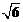 B.
B.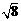 C.
C.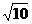 D.
D.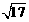
5. (2009台州)大圆半径为6,小圆半径为3,两圆圆心距为10,则这两圆的位置关系为( ▲ )
A.外离 B.外切 C.相交 D.内含
4. (2009德州)将直径为60cm的圆形铁皮,做成三个相同的圆锥容器的侧面(不浪费材料,不计接缝处的材料损耗),那么每个圆锥容器的底面半径为
 (A)10cm (B)30cm (C)45cm (D)300cm
(A)10cm (B)30cm (C)45cm (D)300cm
3.
 A. 15
B. 20 C.15+
A. 15
B. 20 C.15+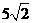 D.15+
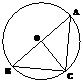
D.15+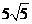 (2009重庆)如图,⊙
(2009重庆)如图,⊙ 是
是 的外接圆,
的外接圆,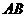 是直径,若
是直径,若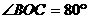 ,则
,则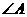 等于( )
等于( )
A.60º B.50º C.40º D.30º
2. (2009福州 )如图3, 是以等边三角形ABC一边AB为半径的四分之一圆周, P为 上任意一点,若AC=5,则四边形ACBP周长的最大值是
1. (2009日照)将直径为60cm的圆形铁皮,做成三个相同的圆锥容器的侧面(不浪费材料,不计接缝处的材料损耗),那么每个圆锥容器的底面半径为
(A)10cm (B)30cm
(C)40cm (D)300cm
12.(09年广东广州)25.(本小题满分14分)
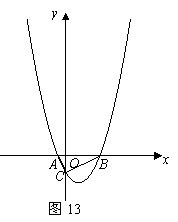
如图13,二次函数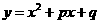 (
(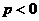 )的图象与
)的图象与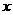 轴交于
轴交于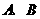 两点,与
两点,与 轴交于点
轴交于点 ,
, 的面积为
的面积为 .
.
(1)求该二次函数的关系式;
(2)过 轴上的一点
轴上的一点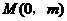 作
作 轴的垂线,若该垂线与
轴的垂线,若该垂线与 的外接圆有公共点,求
的外接圆有公共点,求 的取值范围;
的取值范围;
 (3)在该二次函数的图象上是否存在点
(3)在该二次函数的图象上是否存在点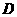 ,使四边形
,使四边形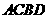 为直角梯形?若存在,求出点
为直角梯形?若存在,求出点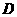 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(09年广东广州25题解析)解:(1)设点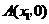 ,
,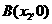 ,其中
,其中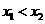 .
.
∵抛物线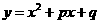 过点
过点 ,
,
∴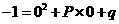 .
.
∴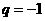 .
.
∴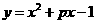 .
.
∵抛物线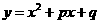 与
与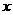 轴交于
轴交于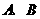 两点,
两点,
∴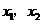 是方程
是方程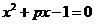 的两个实根.
的两个实根.
求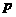 的值给出以下两种方法:
的值给出以下两种方法:
方法1:由韦达定理得: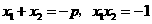 .
.
∵ 的面积为
的面积为 ,
,
∴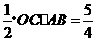 ,即
,即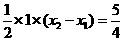 .
.
∴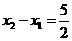 .
.
∴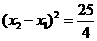 .
.
∵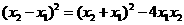 ,
,
∴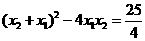 .
.
∴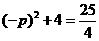 .
.
解得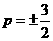 .
.
∵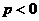 ,
,
∴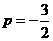 .
.
∴所求二次函数的关系式为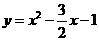 .
.
方法2:由求根公式得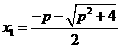 ,
,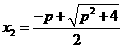 .
.
 .
.
∵ 的面积为
的面积为 ,
,
∴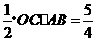 ,即
,即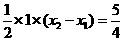 .
.
∴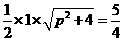 .
.
∴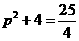 .
.
解得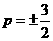 .
.
∵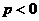 ,
,
∴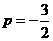 .
.
∴所求二次函数的关系式为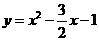 .
.
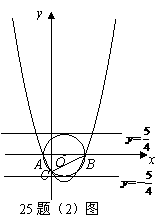
(2)令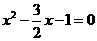 ,解得
,解得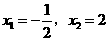 .
.
∴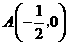 ,
,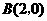 .
.
在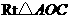 中,
中,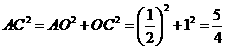 ,
,
在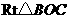 中,
中,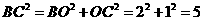 ,
,
 ∵
∵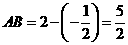 ,
,
∴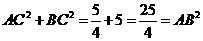 .
.
∴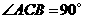 .
.
∴ 是直角三角形.
是直角三角形.
∴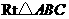 的外接圆的圆心是斜边
的外接圆的圆心是斜边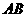 的中点.
的中点.
∴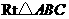 的外接圆的半径
的外接圆的半径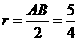 .
.
∵垂线与 的外接圆有公共点,
的外接圆有公共点,
∴ .
.
(3)假设在二次函数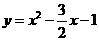 的图象上存在点
的图象上存在点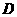 ,使得四边形
,使得四边形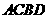 是直角梯形.
是直角梯形.
①若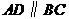 ,设点
,设点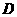 的坐标为
的坐标为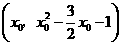 ,
,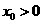 ,
,
 过
过 作
作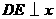 轴,垂足为
轴,垂足为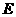 ,如图1所示.
,如图1所示.
求点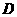 的坐标给出以下两种方法:
的坐标给出以下两种方法:
方法1:在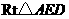 中,
中,
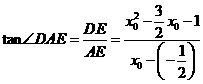 ,
,
在 中,
中,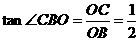 ,
,
∵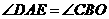 ,
,
∴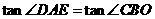 .
.
∴ .
.
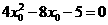 .
.
解得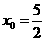 或
或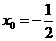 .
.
∵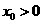 ,
,
∴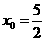 ,此时点
,此时点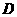 的坐标为
的坐标为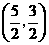 .
.
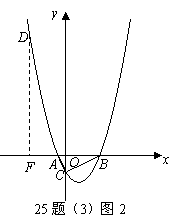 而
而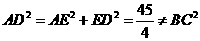 ,因此当
,因此当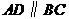 时在抛物线
时在抛物线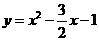 上存在点
上存在点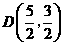 ,使得四边形
,使得四边形 是直角梯形.
是直角梯形.
方法2:在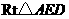 与
与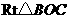 中,
中,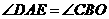 ,
,
∴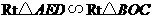 .
.
∴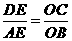 .
.
∴ .
.
以下同方法1.
②若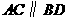 ,设点
,设点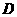 的坐标为
的坐标为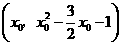 ,
, ,
,
过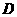 作
作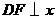 轴,垂足为
轴,垂足为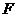 ,如图2所示.
,如图2所示.
在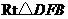 中,
中,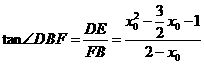 ,
,
在 中,
中,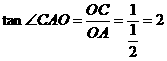 ,
,
∵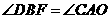 ,
,
∴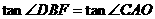 .
.
∴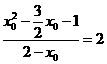 .
.
 .
.
解得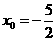 或
或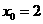 .
.
∵ ,
,
∴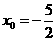 ,此时
,此时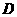 点的坐标为
点的坐标为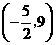 .
.
此时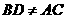 ,因此当
,因此当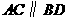 时,在抛物线
时,在抛物线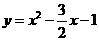 上存在点
上存在点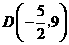 ,使得四边形
,使得四边形 是直角梯形.
是直角梯形.
综上所述,在抛物线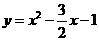 上存在点
上存在点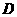 ,使得四边形
,使得四边形 是直角梯形,并且点
是直角梯形,并且点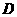 的坐标为
的坐标为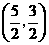 或
或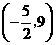 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com