
题目列表(包括答案和解析)
49.(2009四川泰安26)
如图所示,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD。
(1) 求证:BE=AD;
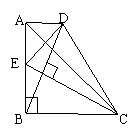 (2)求证:AC是线段ED的垂直平分线;
(2)求证:AC是线段ED的垂直平分线;
(3)△DBC是等腰三角形吗?并说明理由
48.(2009四川眉山22)
在直角梯形ABCD中,AB∥DC,AB⊥BC,∠A=60°,AB=2CD,E、F分别为AB、AD的中点,连结EF、EC、BF、CF。。
⑴判断四边形AECD的形状(不证明);
⑵在不添加其它条件下,写出图中一对全等的三角形,用符号“≌”表示,并证明。
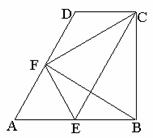 ⑶若CD=2,求四边形BCFE的面积。
⑶若CD=2,求四边形BCFE的面积。
46.(2009浙江杭州22)
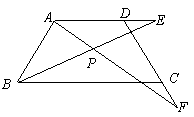 如图,在等腰梯形ABCD中,∠C=60°,AD∥BC,且AD=DC,E、F分别在AD、DC的延长线上,且DE=CF,AF、BE交于点P.
如图,在等腰梯形ABCD中,∠C=60°,AD∥BC,且AD=DC,E、F分别在AD、DC的延长线上,且DE=CF,AF、BE交于点P.
(1)求证:AF=BE;
(2)请你猜测∠BPF的度数,并证明你的结论.
45.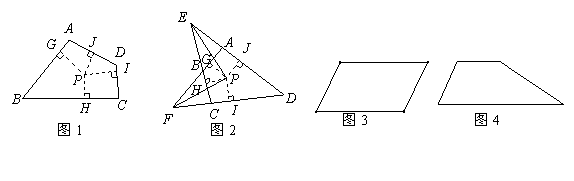 (2009浙江台州23)定义:到凸四边形一组对边距离相等,到另一组对边距离也相等的点叫凸四边形的准内点.如图1,
(2009浙江台州23)定义:到凸四边形一组对边距离相等,到另一组对边距离也相等的点叫凸四边形的准内点.如图1,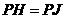 ,
,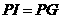 ,则点
,则点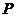 就是四边形
就是四边形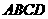 的准内点.
的准内点.
(1)如图2,  与
与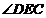 的角平分线
的角平分线 相交于点
相交于点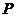 .
.
求证:点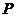 是四边形
是四边形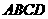 的准内点.
的准内点.
(2)分别画出图3平行四边形和图4梯形的准内点.
(作图工具不限,不写作法,但要有必要的说明)
(3)判断下列命题的真假,在括号内填“真”或“假”.
①任意凸四边形一定存在准内点.( )
②任意凸四边形一定只有一个准内点.( )
③若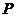 是任意凸四边形
是任意凸四边形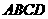 的准内点,则
的准内点,则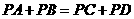
或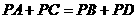 .(
)
.(
)
44.(2009浙江义乌19)
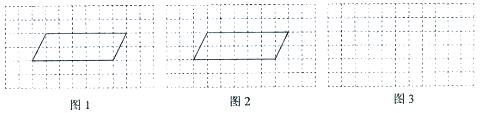
(1)如图1,正方形网格中有一个平行四边形,请在图1中画一条直线把平行四边形分成面积相等的两部分;
(2)把图2中的平行四边形分割成四个全等的四边形(要求在图2中画出分割线),并把所得的四个全等的四边形在图3中拼成一个轴对称图形或中心对称图形,使所得图形与原图形不全等且各个顶点都落在格点上。
温馨提示:作图时,可先使用2B铅笔,确定后必须使用0.5毫米及以上的黑色签字笔涂黑。
43.(2009浙江绍兴22)
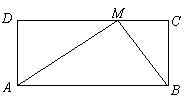
若从矩形一边上的点到对边的视角是直角,则称该点为直角点.例如,如图的矩形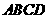 中,点
中,点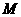 在
在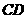 边上,连
边上,连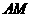 ,
, ,则点
,则点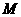 为直角点.
为直角点.
(1)若矩形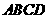 一边
一边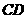 上的直角点
上的直角点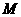 为中点,问该矩形的邻边具有何种数量关系?并说明理由;
为中点,问该矩形的邻边具有何种数量关系?并说明理由;
 (2)若点
(2)若点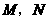 分别为矩形
分别为矩形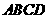 边
边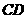 ,
,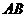 上的直角点,且
上的直角点,且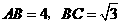 ,求
,求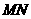 的长.
的长.
42.(2009浙江南充15)
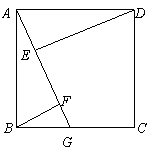 如图ABCD是正方形,点G是BC上的任意一点,
如图ABCD是正方形,点G是BC上的任意一点,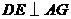 于E,
于E,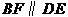 ,交AG于F.
,交AG于F.
求证: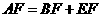 .
.
41.(2009浙江邵阳19)
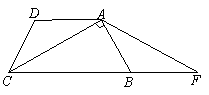
如图在梯形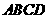 中,
中,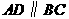 ,
,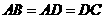 ,
,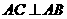 ,将
,将 延长至点
延长至点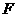 ,使
,使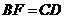 .
.
 (1)求
(1)求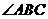 的度数;
的度数;
(2)求证: 为等腰三角形.
为等腰三角形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com