
题目列表(包括答案和解析)
27.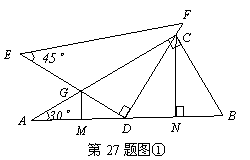 (本题满分8分)
(本题满分8分)
证明:(1)∵∠A=30°,∠ACB=90°,D是AB的中点.
∴BC=BD, ∠B=60°
∴△BCD是等边三角形.····································· 1分
又∵CN⊥DB,
∴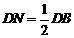 ····················································· 2分
····················································· 2分
∵∠EDF=90°,△BCD是等边三角形.
∴∠ADG=30°,而∠A=30°.
∴GA=GD.
∵GM⊥AB
 ∴
∴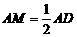 ················································· 3分
················································· 3分
又∵AD=DB
∴AM=DN ··················································· 4分
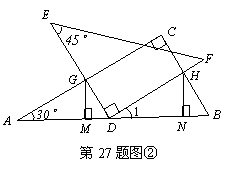
(2)∵DF∥AC
∴∠1=∠A=30°,∠AGD=∠GDH=90°,
∴∠ADG=60°.
∵∠B=60°,AD=DB,
∴△ADG≌△DBH
∴AG=DH,···················································· 6分
又∵∠1=∠A,GM⊥AB,HN⊥AB,
∴△AMG≌△DNH.
∴AM=DN . ·············································· 8分
26.(本题满分7分)
解:(1)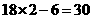 (元) ········································································· 1分
(元) ········································································· 1分
所以一个书包的价格是30元. ··············································································· 2分
(注:用其它方法解出正确答案也给予相应的分值)
(2)设还能为x 名学生每人购买一个书包和一件文化衫,根据题意得:····················· 3分
……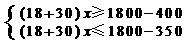 4分
4分
解之得: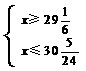
所以不等式组的解集为: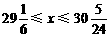 ·························································· 5分
·························································· 5分
∵x为正整数,
∴x=30 ················································································································ 6分
答:剩余经费还能为30名学生每人购买一个书包和一件文化衫.···························· 7分
25、(本题满分7分)
证明:(1)连结OD. ·························································································· 1分
由O、E分别是BC、AC中点得OE∥AB.
∴∠1=∠2,∠B=∠3,又OB=OD.
∴∠2=∠3.
而OD=OC,OE=OE
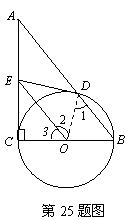 ∴△OCE≌△ODE.
∴△OCE≌△ODE.
∴∠OCE=∠ODE.
又∠C=90°,故∠ODE =90°. ······························· 2分
∴DE是⊙O的切线. ·········································· 3分
(2)在Rt△ODE中,由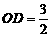 ,DE=2
,DE=2
得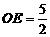 ····························································· 5分
····························································· 5分
又∵O、E分别是CB、CA的中点
∴AB=2·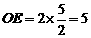
∴所求AB的长是5cm. ····················································································· 7分
24.(本题满分6分)
(1)方法一:作 BC′= BC,DC′=DC.
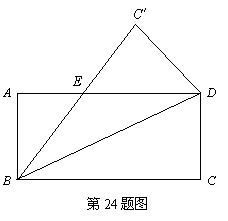 方法二:作∠C′BD=∠CBD,取BC′=BC,连结DC′.
方法二:作∠C′BD=∠CBD,取BC′=BC,连结DC′.
方法三:作∠C′DB=∠CDB,取DC′=DC,连结BC′.
方法四:作C′与C关于BD对称,连结 BC′、DC′.
……
以上各种方法所得到的△BDC′都是所求作的三角形.
只要考生尺规作图正确,痕迹清晰都给3分.
(2)解:∵△C′BD与△CBD关于BD对称,
∴∠EBD=∠CBD.
又∵矩形ABCD的AD∥BC
∴∠EDB=∠CBD.
∴∠EBD=∠EDB,BE = DE.
在Rt△ABE中,AB2+AE2=BE2,而AB=5,BC=12.
∴52+(12-BE)2=BE2 ·············································································· 5分
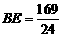
∴所求线段BE的长是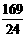 .··········································································· 6分
.··········································································· 6分
23、(本题满分6分)
解:(1)根据题意列表如下:
 |
1 |
2 |
3 |
4 |
|
1 |
|
(1,2) |
(1,3) |
(1,4) |
|
2 |
(2,1) |
|
(2,3) |
(2,4) |
|
3 |
(3,1) |
(3,2) |
|
(3,4) |
|
4 |
(4,1) |
(4,2) |
(4,3) |
|
由以上表格可知:有12种可能结果 ·········································································· 3分
(注:用其它方法得出正确的结果,也给予相应的分值)
(2)在(1)中的12种可能结果中,两个数字之积为奇数的只有2种,
所以,P(两个数字之积是奇数)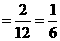 .······························································ 6分
.······························································ 6分
22.(本题满分6分)
解:延长AC交 ON于点E,········································· 1分
 ∵AC⊥ON,
∵AC⊥ON,
∠OEC=90°,································································ 2分
∵四边形ABCD是矩形,
∴∠ABC=90°,AD=BC,
又∵∠OCE=∠ACB,
∴∠BAC=∠O=25°, ··················································· 3分
在Rt△ABC中,AC=3,
∴BC=AC·sin25°≈1.27 ················································· 5分
∴AD≈1.27 ································································ 6分
(注:只要考生用其它方法解出正确的结果,给予相应的分值)
21.(本题共2小题;第(1)题5分,第(2)题5分,共10分)
(1) 解:原式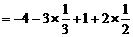 ································································· 4分
································································· 4分
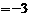 ······························································································ 5分
······························································································ 5分
(2) 解:方程两边同乘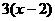 ,得 ································································· 1分
,得 ································································· 1分
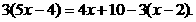 ································································· 3分
································································· 3分
解这个方程,得 x=2 ············································································· 4分
检验:当x=2时,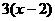 =0,所以x=2是增根,原方程无解.················ 5分
=0,所以x=2是增根,原方程无解.················ 5分
9. 45 ; 10.2 ; 11.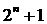 ; 12.
; 12.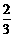
5. 甲 ; 6.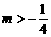 ; 7.
; 7.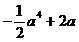 ; 8. 13 ;
; 8. 13 ;
1. 2009 ; 2.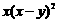 ; 3. 2.124×104 ; 4.
; 3. 2.124×104 ; 4. 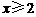 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com