
题目列表(包括答案和解析)
22.(河南) (10分)某家电商场计划用32400元购进“家电下乡”指定产品中的电视机、冰箱、洗衣机共l5台.三种家电的进价和售价如下表所示:

(1)在不超出现有资金的前提下,若购进电视机的数量和冰箱的数量相同,洗衣机数量不大于电视机数量的一半,商场有哪几种进货方案?
(2)国家规定:农民购买家电后,可根据商场售价的13%领取补贴.在(1)的条件下.
如果这15台家电全部销售给农民,国家财政最多需补贴农民多少元?
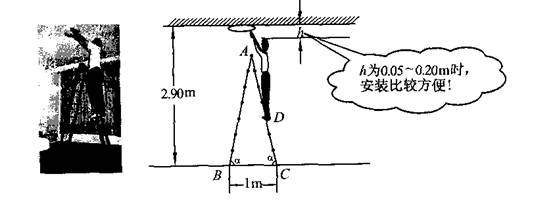
20.(河南)(9分)如图所示,电工李师傅借助梯子安装天花板上距地面2 .90m的顶灯.已知梯子由两个相同的矩形面组成,每个矩形面的长都被六条踏板七等分,使用时梯脚的固定跨度为1m.矩形面与地面所成的角α为78°.李师傅的身高为l.78m,当他攀升到头顶距天花板0.05-0.20m时,安装起来比较方便.他现在竖直站立在梯子的第三级踏板上,请你通过计算判断他安装是否比较方便?
(参考数据:sin78°≈0.98,cos78°≈0.21,tan78°≈4.70.)
1.1 建立一元二次方程模型 同步练习
(时量:40分钟,满分:100分)
课标要求:
1 了解一元二次方程的概念;
2 了解一元二次方程的一般形式,会把一元二次方程化成一般形式,能写出一般形式的二次项系数、一次项系数和常数项。
重点:经历建立一元二次模型的过程,会把一元二次方程化为一般形式。
难点:把实际问题转化为一元二次方程模型。
一 选择题(每小题 5分,共 25 分)
1下列方程中,一元二次方程有( )
(1)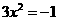 (2)
(2)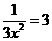 (3)
(3)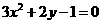 (4)a
(4)a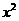 -2x+1=0(a是实数)
-2x+1=0(a是实数)
(5)2x(3x+2)=(x+1)(6x-3)
A 1个 B 2个 C 3个 D 4个
2 把方程:(2x-1)(2x+1)=
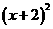 化成一般形式后,二次项系数、一次项系数、常数项分别是( )
化成一般形式后,二次项系数、一次项系数、常数项分别是( )
A 5,-4,-5; B 3,-4,-5 C 3 ,-4 ,5 D 3, 4 -5
3 关于x的一元二次方程:(a-3)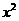 +x+
+x+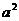 -9=0,有一个根为0,则a=
( )
-9=0,有一个根为0,则a=
( )
A 3 B -3 C ±3 D 无法确定
4 (2007 天津)下列方程是关于x的一元二次方程的是( )
A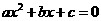 B
B 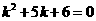 ,
,
C 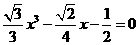 , D
, D 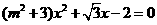
5 某“希望学校”初中三年级1班部分同学利用课后时间上街为四川灾区募捐,他们发现人们捐款热情很高,捐款数第三天比第一天翻了2翻,若设这三天平均每天增加率为x,依题意可得方程( )
A 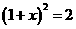 , B
, B 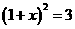 , C
, C 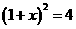 D
D 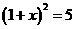
二 填空题(每小题 5分,共 25 分)
6方程
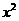 -
-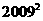 =0的各项项系数乘积的为____.
=0的各项项系数乘积的为____.
7若关于x的一元二次方程(m-2)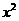 +3x+
+3x+ -4=0的常数项为0,则m的值为_____
-4=0的常数项为0,则m的值为_____
8关于x的方程: (a-1) 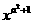 +3ax-3=0,当a为____值时它是一元二次方程,当a为____值时,它为一元一次方程。
+3ax-3=0,当a为____值时它是一元二次方程,当a为____值时,它为一元一次方程。
9在方程:①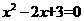 ,②
,②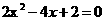 ,③
,③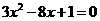 ④
④ 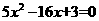 中二次项的系数具有一个共同点特点,请你用代数式把这个特点表示出来:_______________
中二次项的系数具有一个共同点特点,请你用代数式把这个特点表示出来:_______________
10如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC向点C以2cm/s的速度移动,如果P、Q分别从A,B同时出发,x秒后△PBQ的面积等于4 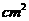 ,依题意可以得方程:___________________________________________
,依题意可以得方程:___________________________________________
三 解答题(11至14题每题10分,共50分)
11把下列方程化成一般形式,并指出二次项的系数、一次项的系数、常数项
(1)3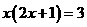 (2)
(2) 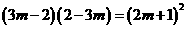
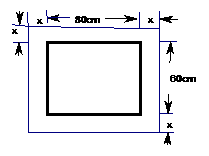 12在一副长为60cm,宽为80cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使挂图的面积为6300
12在一副长为60cm,宽为80cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使挂图的面积为6300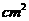 ,设金色纸边的宽为xcm,请你依题意列出方程。
,设金色纸边的宽为xcm,请你依题意列出方程。
13(2006 长沙市) 某科技公司研制成功一种新产品决定向银行贷款200万元资金用于生产这种产品,签订合同上约定两年到期时一次性还本付息,利息为本金的8%,该产品投放市场后,由于产销对路,使公司在两年到期除还清贷款的本金和利息外,还盈利72万元,若该公司在生产期间每年比上一年资金增长的百分数相同,求这个百分数。(只要求设好未知数,列出方程)
14(2007年,安微)据报道我省农作物秸杆的资源巨大,但合理利用量十分有限,2006年度利用率只有30%,大部分的秸杆被焚烧了,假定我省每年产出的农作物秸秆总量不变,且合理利用量的增长率相同,要使2008年的利用率提高到60%求每年的增加率,设这个增加率为x,请你依据题意列出方程
15商场销售某种新商品,每件进价为120元,在试销期间发现,当每件商品售价为130元
每天可以销售70件,当每件商品售价高于130元时,每涨一元,日销量就减少1件,据此规律, (1)如果每件定价为170元,每天可以销售多少件,每件盈利多少元,每天盈利多少元(提示:盈利=售价-进价)
(2)如果每件定价为x元(x>130),商场日盈利1600元,可以得到关于x的方程为_______________
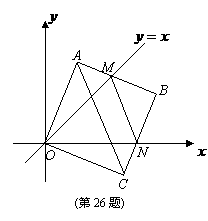
26. (12分)
在平面直角坐标中,边长为2的正方形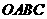 的两顶点
的两顶点 、
、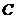 分别在
分别在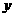 轴、
轴、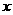 轴的正半轴上,点
轴的正半轴上,点 在原点.现将正方形
在原点.现将正方形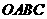 绕
绕 点顺时针旋转,当
点顺时针旋转,当 点第一次落在直线
点第一次落在直线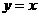 上时停止旋转,旋转过程中,
上时停止旋转,旋转过程中,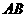 边交直线
边交直线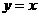 于点
于点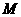 ,
, 边交
边交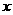 轴于点
轴于点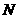 (如图).
(如图).
(1)求边 在旋转过程中所扫过的面积;
在旋转过程中所扫过的面积;
 (2)旋转过程中,当
(2)旋转过程中,当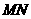 和
和 平行时,求正方形
平行时,求正方形
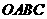 旋转的度数;
旋转的度数;
(3)设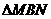 的周长为
的周长为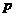 ,在旋转正方形
,在旋转正方形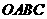
的过程中,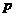 值是否有变化?请证明你的结论.
值是否有变化?请证明你的结论.
25.(9分)
某体育用品商店购进一批滑板,每件进价为100元,售价为130元,每星期可卖出80件.商家决定降价促销,根据市场调查,每降价5元,每星期可多卖出20件.
(1)求商家降价前每星期的销售利润为多少元?
(2)降价后,商家要使每星期的销售利润最大,应将售价定为多少元?最大销售利润是多少?
24.(9分)
如图,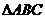 中,
中,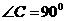 ,
,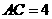 ,
,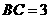 .半径为1的圆的圆心
.半径为1的圆的圆心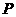 以1个单位/
以1个单位/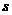 的速度由点
的速度由点 沿
沿 方向在
方向在 上移动,设移动时间为
上移动,设移动时间为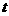 (单位:
(单位: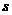 ).
).
(1)当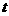 为何值时,⊙
为何值时,⊙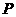 与
与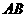 相切;
相切;
(2)作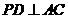 交
交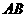 于点
于点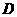 ,如果⊙
,如果⊙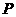 和线段
和线段 交于点
交于点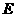 ,证明:当
,证明:当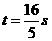 时,四边形
时,四边形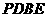 为平行四边形.
为平行四边形.
22.(8分)
坐落在山东省汶上县宝相寺内的太子灵踪塔始建于北宋(公元1112年),为砖彻八角形十三层楼阁式建筑.数学活动小组开展课外实践活动,在一个阳光明媚的上午,他们去测量太子灵踪塔的高度,携带的测量工具有:测角仪、皮尺、小镜子.
(1)小华利用测角仪和皮尺测量塔高.
图1为小华测量塔高的示意图.她先在塔前的平地上选择一点 ,用测角仪测出看塔顶
,用测角仪测出看塔顶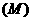 的仰角
的仰角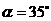 ,在
,在 点和塔之间选择一点
点和塔之间选择一点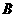 ,测出看塔顶
,测出看塔顶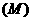 的仰角
的仰角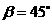 ,然后用皮尺量出
,然后用皮尺量出 、
、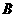 两点的距离为
两点的距离为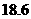 m,自身的高度为
m,自身的高度为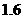 m.请你利用上述数据帮助小华计算出塔的高度(
m.请你利用上述数据帮助小华计算出塔的高度(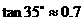 ,结果保留整数).
,结果保留整数).

(2)如果你是活动小组的一员,正准备测量塔高,而此时塔影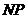 的长为
的长为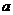 m(如图2),你能否利用这一数据设计一个测量方案?如果能,请回答下列问题:
m(如图2),你能否利用这一数据设计一个测量方案?如果能,请回答下列问题:
①在你设计的测量方案中,选用的测量工具是: ;
②要计算出塔的高,你还需要测量哪些数据?
.
21.(8分)
作为一项惠农强农应对当前国际金融危机、拉动国内消费需求的重要措施,“家电下乡”工作已经国务院批准从2008年12月1日起在我市实施.我市某家电公司营销点自去年12月份至今年5月份销售两种不同品牌冰箱的数量如下图:
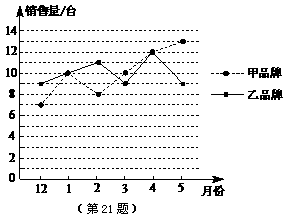
(1)完成下表:
|
|
平均数 |
方差 |
|
甲品牌销售量/台 |
10 |
|
|
乙品牌销售量/台 |
|
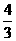 |
(2)请你依据折线图的变化趋势,对营销点今后的进货情况提出建议.
20.(6分)
解方程: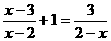 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com