
题目列表(包括答案和解析)
2、(2009,宁波)下列四个数中,比0小的数是 ( )D
A.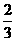 B.
B.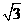 C.
C.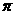 D.
D.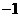
1、(2009,宁波)实数8的立方根是 .2
5.5 < x <8 .
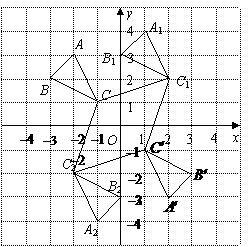
 (2009,河南)如图所示,在平面直角坐标系中,点A、B的坐标分别为(﹣2,0)和(2,0).月牙①绕点B顺时针旋转900得到月牙②,则点A的对应点A’的坐标为
[ ]B
(2009,河南)如图所示,在平面直角坐标系中,点A、B的坐标分别为(﹣2,0)和(2,0).月牙①绕点B顺时针旋转900得到月牙②,则点A的对应点A’的坐标为
[ ]B
(A)(2,2) (B)(2,4)
(C)(4,2) (D)(1,2)
 (2009,牡丹江)
(2009,牡丹江) 在如图所示的平面直角坐标系中,将
在如图所示的平面直角坐标系中,将 向右平移3个单位长度后得
向右平移3个单位长度后得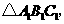 再将
再将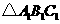 绕点
绕点 旋转
旋转 后得到
后得到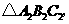 则下列说法正确的是( )D
则下列说法正确的是( )D
A. 的坐标为
的坐标为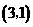 B.
B.
C.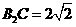 D.
D.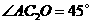
(2009,齐齐哈尔)如图,在平面直角坐标系中, 的顶点坐标为
的顶点坐标为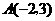 、
、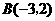 、
、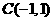 .
.
(1)若将 向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的
向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的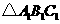 ;
;
(2)画出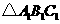 绕原点旋转
绕原点旋转 后得到的
后得到的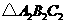 ;
;
(3)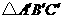 与
与 是中心对称图形,请写出对称中心的坐标:___________;
是中心对称图形,请写出对称中心的坐标:___________;
(4)顺次连结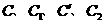 ,所得到的图形是轴对称图形吗?
,所得到的图形是轴对称图形吗?
 画出平移后的图形,
画出平移后的图形,
画出旋转后的图形
写出坐标(0,0),
答出“是轴对称图形”
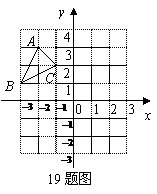
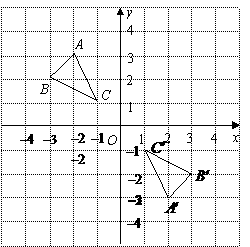
(2009,哈尔滨)如图,在每个小正方形的边长均为1个单位长度的方格纸中,有一
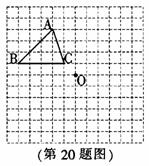 个△ABC和一点O,△ABC的顶点和点O均与小正方形的顶点重合.
个△ABC和一点O,△ABC的顶点和点O均与小正方形的顶点重合.
(1)在方格纸中,将△ABC向下平移5个单位长度得到△A1B1C1,
请画出△A1B1C1
(2)在方格纸中,将△ABC绕点O旋转180°得到△A2B2C2,
请画出△A2B2C2。
(2009,佳木斯)如图,A、B、C为一个平行四边形的三个顶点,且A、B、C三点的坐标分别为(3,3)、(6,4)、(4,6).
(1)请直接写出这个平行四边形第四个顶点的坐标;
(2)求这个平行四边形的面积.
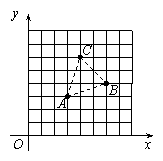
(2009,武汉)如图,已知 的三个顶点的坐标分别为
的三个顶点的坐标分别为 、
、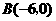 、
、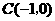 .
.
(1)请直接写出点 关于
关于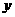 轴对称的点的坐标;
轴对称的点的坐标;
(2)将 绕坐标原点
绕坐标原点 逆时针旋转90°.画出图形,直接写出点
逆时针旋转90°.画出图形,直接写出点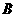 的对应点的坐标;
的对应点的坐标;
(3)请直接写出:以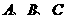 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点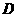 的坐标.
的坐标.

解:(1)(2,3);
(2)图形略.(0,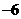 );
);
(3)(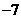
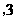 )或
)或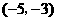 或
或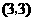 .
.
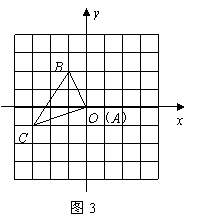
(2009,襄樊)如图3,在边长为1的正方形网格中,将 向右平移两个单位长度得到
向右平移两个单位长度得到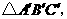 则与点
则与点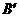 关于
关于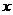 轴对称的点的坐标是( )D
轴对称的点的坐标是( )D
A.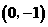 B.
B.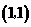 C.
C.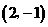 D.
D.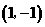
(2009,朝阳)在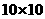 的网格纸上建立平面直角坐标系如图所示,在
的网格纸上建立平面直角坐标系如图所示,在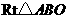 中,
中,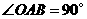 ,且点
,且点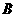 的坐标为
的坐标为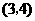 .
.
(1)画出 向左平移3个单位后的
向左平移3个单位后的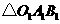 ,写出点
,写出点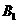 的坐标;
的坐标;

 (2)画出
(2)画出 绕点
绕点 顺时针旋转
顺时针旋转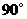 后的
后的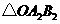 ,并求点
,并求点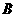 旋转到点
旋转到点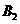 时,点
时,点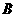 经过的路线长(结果保留
经过的路线长(结果保留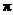 )
)
解:(1)画图)
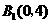
(2)画图
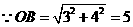
 点
点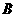 旋转到点
旋转到点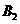 时,经过的路线长为
时,经过的路线长为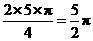
(2009,沈阳)如图,在平面直角坐标系中,已知点A(1,0)和点B(0,),点
C在坐标平面内.若以A、B、C为顶点构成的三角形是等腰
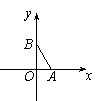 三角形,且底角为30º,则满足条件的点C有 个.
三角形,且底角为30º,则满足条件的点C有 个.
(2009,青岛)一艘轮船从港口 出发,以15海里/时的速度沿北偏东60°的方向航行4小时后到达A处,此时观测到其正西方向50海里处有一座小岛B.若以港口
出发,以15海里/时的速度沿北偏东60°的方向航行4小时后到达A处,此时观测到其正西方向50海里处有一座小岛B.若以港口 为坐标原点,正东方向为
为坐标原点,正东方向为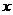 轴的正方向,正北方向为
轴的正方向,正北方向为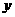 轴的正方向,1海里为1个单位长度建立平面直角坐标系(如图),则小岛B所在位置的坐标是( )A
轴的正方向,1海里为1个单位长度建立平面直角坐标系(如图),则小岛B所在位置的坐标是( )A
A.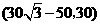 B.
B.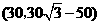 C.
C.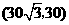 D.
D.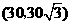
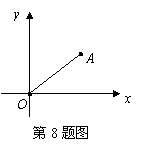
(2009,达州)在平面直角坐标系中,设点P到原点O的距离为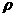 ,OP与x轴正方向的夹角为
,OP与x轴正方向的夹角为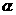 ,则用
,则用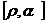 表示点P的极坐标,显然,点P的极坐标与它的坐标存在一一对应关系.例如:点P的坐标为(1,1),则其极坐标为
表示点P的极坐标,显然,点P的极坐标与它的坐标存在一一对应关系.例如:点P的坐标为(1,1),则其极坐标为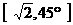 .若点Q的极坐标为
.若点Q的极坐标为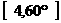 ,则点Q的坐标为 A
,则点Q的坐标为 A
A.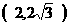 B.
B.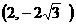 C.(2
C.(2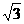 ,2) D.(2,2)
,2) D.(2,2)
(2009,乌鲁木奇)在平面直角坐标系中,点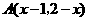 在第四象限,则实数
在第四象限,则实数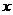 的取值范围是
.
的取值范围是
.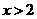
(2009,云南)在平面直角坐标系中,已知3个点的坐标分别为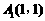 、
、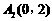 、
、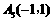 . 一只电子蛙位于坐标原点处,第1次电子蛙由原点跳到以
. 一只电子蛙位于坐标原点处,第1次电子蛙由原点跳到以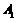 为对称中心的对称点
为对称中心的对称点 ,第2次电子蛙由
,第2次电子蛙由 点跳到以
点跳到以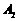 为对称中心的对称点
为对称中心的对称点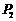 ,第3次电子蛙由
,第3次电子蛙由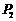 点跳到以
点跳到以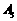 为对称中心的对称点
为对称中心的对称点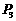 ,…,按此规律,电子蛙分别以
,…,按此规律,电子蛙分别以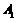 、
、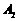 、
、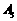 为对称中心继续跳下去.问当电子蛙跳了2009次后,电子蛙落点的坐标是
为对称中心继续跳下去.问当电子蛙跳了2009次后,电子蛙落点的坐标是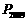 (_______ ,_______).
(_______ ,_______).
(−2,2)
(2009,嘉兴)如图,在直角坐标系中,已知点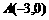 ,
,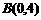 ,对△
,对△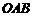 连续作旋转变换,依次得到三角形①、②、③、④…,则三角形⑩的直角顶点的坐标为 ▲ .
连续作旋转变换,依次得到三角形①、②、③、④…,则三角形⑩的直角顶点的坐标为 ▲ .
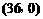
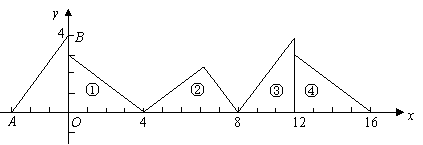
(2009,宁波)以方程组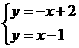 的解为坐标的点
的解为坐标的点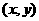 在平面直角坐标系中的位置是( )A
在平面直角坐标系中的位置是( )A
A.第一象限 B.第二象限 C.第三象限 D.第四象限
20.(孝感)(本题满分8分)
三个牧童A、B、C在一块正方形的牧场上看守一群牛,为保证公平合理,他们商量将牧场划分为三块分别看守,划分的原则是:①每个人看守的牧场面积相等;②在每个区域内,各选定一个看守点,并保证在有情况时他们所需走的最大距离(看守点到本区域内最远处的距离)相等.按照这一原则,他们先设计了一种如图1的划分方案:把正方形牧场分成三块相等的矩形,大家分头守在这三个矩形的中心(对角线交点),看守自己的一块牧场.
过了一段时间,牧童B和牧童C又分别提出了新的划分方案.
牧童B的划分方案如图2:三块矩形的面积相等,牧童的位置在三个小矩形的中心.
牧童C的划分方案如图3:把正方形的牧场分成三块矩形,牧童的位置在三个小矩形的中心,并保证在有情况时三个人所需走的最大距离相等.
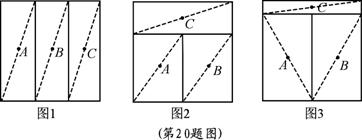
请回答:
(1)牧童B的划分方案中,牧童 ▲ (填A、B或C)在有情况时所需走的最大距离较远;(3分)
(2)牧童C的划分方案是否符合他们商量的划分原则?为什么?(提示:在计算时可取正方形边长为2)(5分)
26.(哈尔滨)(本题8分)
跃壮五金商店准备从宁云机械厂购进甲、乙两种零件进行销售.若每个甲种零件的进价比每个乙种零件的进价少2元,且用80元购进甲种零件的数量与用100元购进乙种零件的数量相同.
(1)求每个甲种零件、每个乙种零件的进价分别为多少元?
(2)若该五金商店本次购进甲种零件的数量比购进乙种零件的数量的3倍还少5个,购进两种零件的总数量不超过95个,该五金商店每个甲种零件的销售价格为12元,每个乙种零件的销售价格为15元,则将本次购进的甲、乙两种零件全部售出后,可使销售两种零件的总利润(利润=售价-进价)超过371元,通过计算求出跃壮五金商店本次从宁云机械厂购进甲、乙两种零件有几种方案?请你设计出来.
26、某土产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售。按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满,根据下表提供的信息,
解答以下问题
(1)设装运甲种土特产的车辆数为x,装运乙种土特产的车辆数为y,求y与x之间的函数关系式.
(2)如果装运每种土特产的车辆都不少于3辆,那么车辆的安排方案有几种?并写出每种安排方案。
(3)若要使此次销售获利最大,应采用(2)中哪种安排方案?并求出最大利润的值。
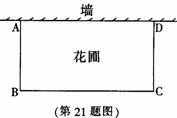 (哈尔滨)21.(本题5分)
(哈尔滨)21.(本题5分)
张大爷要围成一个矩形花圃.花圃的一边利用足够长的墙另三
边用总长为32米的篱笆恰好围成.围成的花圃是如图所示的矩形
ABCD.设AB边的长为x米.矩形ABCD的面积为S平方米.
(1)求S与x之间的函数关系式(不要求写出自变量x的取值范围)
(2)当x为何值时,S有最大值?并求出最大值.
(参考公式:二次函数y=ax2+bx+c(a≠0),当x=-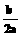 时,y最大(小)值=
时,y最大(小)值=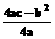 )
)
18.(山东潍坊)(本小题满分8分)
某蔬菜加工厂承担出口蔬菜加工任务,有一批蔬菜产品需要装入某一规格的纸箱.供应这种纸箱有两种方案可供选择:
方案一:从纸箱厂定制购买,每个纸箱价格为4元;
方案二:由蔬菜加工厂租赁机器自己加工制作这种纸箱,机器租赁费按生产纸箱数收取.工厂需要一次性投入机器安装等费用16000元,每加工一个纸箱还需成本费2.4元.
(1)若需要这种规格的纸箱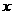 个,请分别写出从纸箱厂购买纸箱的费用
个,请分别写出从纸箱厂购买纸箱的费用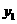 (元)和蔬菜加工厂自己加工制作纸箱的费用
(元)和蔬菜加工厂自己加工制作纸箱的费用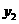 (元)关于
(元)关于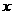 (个)的函数关系式;
(个)的函数关系式;
(2)假设你是决策者,你认为应该选择哪种方案?并说明理由.
(鄂州市)
|
每吨土特产获利(百元) |
12 |
16 |
10 |
19.(四川凉山)我国沪深股市交易中,如果买、卖一次股票均需付交易金额的0.5%作费用.张先生以每股5元的价格买入“西昌电力”股票1000股,若他期望获利不低于1000元,问他至少要等到该股票涨到每股多少元时才能卖出?(精确到0.01元)
28.(山西太原)(本小题满分9分)
 、
、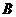 两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往
两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往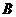 城,乙车驶往
城,乙车驶往 城,甲车在行驶过程中速度始终不变.甲车距
城,甲车在行驶过程中速度始终不变.甲车距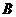 城高速公路入口处的距离
城高速公路入口处的距离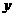 (千米)与行驶时间
(千米)与行驶时间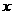 (时)之间的关系如图.
(时)之间的关系如图.
(1)求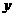 关于
关于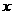 的表达式;
的表达式;
(2)已知乙车以60千米/时的速度匀速行驶,设行驶过程中,两车相距的路程为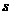 (千米).请直接写出
(千米).请直接写出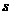 关于
关于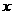 的表达式;
的表达式;
 (3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为
(3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为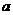 (千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度
(千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度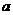 .在下图中画出乙车离开
.在下图中画出乙车离开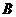 城高速公路入口处的距离
城高速公路入口处的距离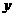 (千米)与行驶时间
(千米)与行驶时间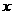 (时)之间的函数图象.
(时)之间的函数图象.
(陕西) 21.(本题满分8分)
在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发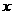 (h)时,汽车与甲地的距离为
(h)时,汽车与甲地的距离为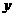 (km),
(km),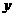 与
与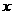 的函数关系如图所示.
的函数关系如图所示.
根据图象信息,解答下列问题:
(1)这辆汽车的往、返速度是否相同?请说明理由;
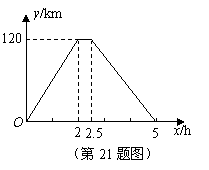 (2)求返程中
(2)求返程中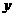 与
与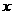 之间的函数表达式;
之间的函数表达式;
(3)求这辆汽车从甲地出发4h时与甲地的距离.
21.(广东东营) (本题满分9分)
为了贯彻落实国务院关于促进家电下乡的指示精神,有关部门自2007年12月底起进行了家电下乡试点,对彩电、冰箱(含冰柜)、手机三大类产品给予产品销售价格13%的财政资金直补.企业数据显示,截至2008年12月底,试点产品已销售350万台(部),销售额达50亿元,与上年同期相比,试点产品家电销售量增长了40%.
(1)求2007年同期试点产品类家电销售量为多少万台(部)?
(2)如果销售家电的平均价格为:彩电每台1500元,冰箱每台2000元,手机每部800元,已知销售的冰箱(含冰柜)数量是彩电数量的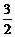 倍,求彩电、冰箱、手机三大类产品分别销售多少万台(部),并计算获得的政府补贴分别为多少万元?
倍,求彩电、冰箱、手机三大类产品分别销售多少万台(部),并计算获得的政府补贴分别为多少万元?
(山西太原) 23.(本小题满分6分)
某公司计划生产甲、乙两种产品共20件,其总产值 (万元)满足:1150<
(万元)满足:1150< <1200,相关数据如下表.为此,公司应怎样设计这两种产品的生产方案.
<1200,相关数据如下表.为此,公司应怎样设计这两种产品的生产方案.
|
产品名称 |
每件产品的产值(万元) |
|
甲 |
45 |
|
乙 |
75 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com