
题目列表(包括答案和解析)
2. (2007.内江) 用配方法解方程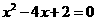 ,下列配方正确的是( )
,下列配方正确的是( )
A 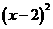 =2 B
=2 B 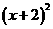 =2 C
=2 C
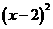 = -2 D
= -2 D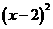 =6
=6
1. 如果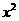 +8x+a=
+8x+a= 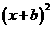 ,那么( )
,那么( )
A a=4, b=16 B a=4 , b=4 C a=2 , b=4 D a =16 , b=4
1.2 一元二次方程的算法 配方法(1) 同步练习
考标要求
会用配方法解二次项系数为1的一元二次方程
重点:用配方法解二次项系数为1的一元二次方程
难点:用配方法把一元二次方程化成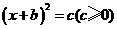 的形式。
的形式。
一 选择题(每小题5分,共25分)
1.2 一元二次方程的算法(2)配方法 同步练习
考标要求
掌握用配方法解二次项系数不为1的一元二次方程的解法。
重点:用配方法解二次项系数不为1的一元二次方程
难点:理解把二次项系数不为1转化为1再配方的过程
一 选择题(每小题5分,共25分)
1 下面是甲、乙、丙三位同学用配方法解一元二次方程的配方过程:
甲: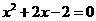 解:
解: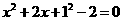 ,
,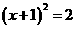
乙: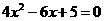 解:
解: ,
,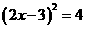
丙: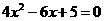 解:
解: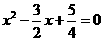 ,
,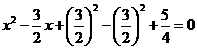 ,
, 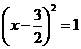
其中正确的是( )
A 甲 B 乙 C 丙 D 都不正确
2 解一元二次方程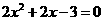 ,配方正确的是( )
,配方正确的是( )
A 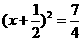 B
B 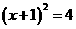 C
C 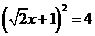 D
D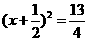
3 把方程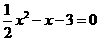 配方后得到的方程是( )
配方后得到的方程是( )
A 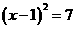 ,B
,B 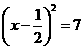 C
C 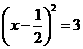 D
D 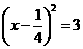
4 已知:,则方程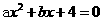 的解为( )
的解为( )
A 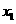 =4,
=4,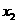 =-1 B
=-1 B 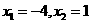 C
C 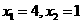 D
D 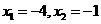
5 用配方法可以求得,不论x为何实数,代数式: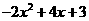 的值( )
的值( )
A 总不少于5,B 总不大于5 C 总不少于8 ,D 总不大于8
二 填空题(每小题5分,共25分)
6 用配方法解方程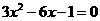 ,先应把二次项的系数化为____,因此需要两边同除以_______;
,先应把二次项的系数化为____,因此需要两边同除以_______;
7 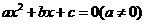 经过配方得到:
经过配方得到: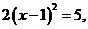 则a=_____b= ___,C=______;
则a=_____b= ___,C=______;
8 用配方法把方程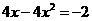 化成
化成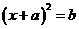 的形式,其中a=___,b=_____
的形式,其中a=___,b=_____
9 已知x= -1是方程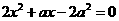 的一个根,则a=_____
的一个根,则a=_____
10 把方程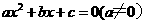 配方,先两边同除以a得:
配方,先两边同除以a得: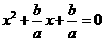 ,然后应把方程左边加上______,再减去________。
,然后应把方程左边加上______,再减去________。
三 解答题(11题16分,12、13各7分,14、15题各10分)
11 用配方法解下列方程
(1) 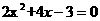 (2)(2x+1)(x-3)=1
(2)(2x+1)(x-3)=1
(3)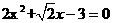 (4)
(4)
12代数式4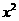 +8x+5有最大值还是有最少值?是多少
+8x+5有最大值还是有最少值?是多少
13 15 任何一个一元二次方程 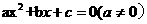 都可以配方化成
都可以配方化成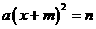 的形式吗?如果能写出配方过程,如果不能,举出反例。
的形式吗?如果能写出配方过程,如果不能,举出反例。
14一名跳水运动员进行10米跳台跳水训练,在正常情况下,运动员必须在距离水面5m以前完成规定的翻滚动作,并且调整好如水姿势,否则就容易出现失误,假设运动员起跳后,运动时间t(s)和运动员距离水面的高度h(m)满足关系:h=10+2.5t-5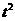 ,那么他最多有多长时间完成规定动作?(精确到0.1s)
,那么他最多有多长时间完成规定动作?(精确到0.1s)
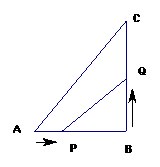 15如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC向点C以2cm/s的速度移动,如果P、Q分别从A,B同时出发那么几秒后△PBQ的面积等于4
15如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC向点C以2cm/s的速度移动,如果P、Q分别从A,B同时出发那么几秒后△PBQ的面积等于4 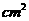 ,
,
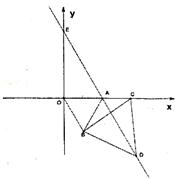
25.  在如图所示的平面直角坐标系中,
在如图所示的平面直角坐标系中, ,
,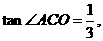 OB的长是方程
OB的长是方程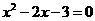 的解,二次函数
的解,二次函数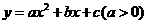 的图像的顶点为D,且经过A、B、C三点,反比例函数
的图像的顶点为D,且经过A、B、C三点,反比例函数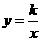 的图像经过D点。
的图像经过D点。
(1)求这两个函数解析式
(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标:若不存在,请说明理由:
(3)若平行于x轴的直线,与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度:
(4)在坐轴上是否存在一点P,使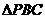 是等腰三角形,若存在,直接写出所有满足条件的点P的坐标:若不存在,请说明理由。
是等腰三角形,若存在,直接写出所有满足条件的点P的坐标:若不存在,请说明理由。

24.(10分)如图,扇形OAB的半径OA=3,圆心角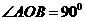 ,点C是
,点C是 上异于A、B的动点,过点C作
上异于A、B的动点,过点C作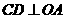 于点D,作
于点D,作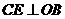 于点E,连结DE,点G、H在线段DE上,且DG=GH=HE
于点E,连结DE,点G、H在线段DE上,且DG=GH=HE
(1)求证:四边形OGCH是平行四边形
(2)当点C在 运动时,在CD、CG、DG中,是否存在长度不变的线段?若存在,请求出该线段的长度
运动时,在CD、CG、DG中,是否存在长度不变的线段?若存在,请求出该线段的长度
 (3)求证:
(3)求证: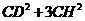 是定值
是定值
23.(10分)“5 12”汶川大地震后,某健身器材销售公司通过当地“红十字会”向灾区献爱心,捐出了五月份全部销售利润,已知该公司五月份只售出甲、乙、丙三种型号器材若干台,每种型号器材不少于8台,五月份支出包括这批器材进贷款64万元和其他各项支出,(含人员工资和杂项开支)3.8万元,这三种器材的进价和售价如下表,人员工资
12”汶川大地震后,某健身器材销售公司通过当地“红十字会”向灾区献爱心,捐出了五月份全部销售利润,已知该公司五月份只售出甲、乙、丙三种型号器材若干台,每种型号器材不少于8台,五月份支出包括这批器材进贷款64万元和其他各项支出,(含人员工资和杂项开支)3.8万元,这三种器材的进价和售价如下表,人员工资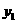 (万元)和杂项支出
(万元)和杂项支出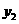 (万元)分别与总销售量x(台)成一次函数关系(如图)。
(万元)分别与总销售量x(台)成一次函数关系(如图)。
(1)求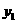 与x的函数解析式:
与x的函数解析式:
(2)求五月份该公司的总销售量:
(3)设公司五月份售出甲种型号器材t台,五月份总销售利润为W(万元),求W与t的函数关系式:(销售利润=销售额-进价-其他各项支出)
(4)请推测该公司这次向灾区捐款金额的最大值
|
型号 |
甲 |
乙 |
丙 |
|
进价(万元/台) |
0.9 |
1.2 |
1.1 |
|
售价(万元/台) |
1.2 |
1.6 |
1.3 |

22.(10分)某私立中学准备招聘教职员工60名,所有员工的月工资情况如下:
|
员工 |
管理人员 |
教学人员 |
|||||
|
人员结构 |
校长 |
副校长 |
部处主任 |
教研组长 |
高级教师 |
中级教师 |
初级教师 |
|
员工人数/人 |
1 |
2 |
4 |
10 |
|
|
|
|
每月工资/元 |
20000 |
17000 |
2500 |
2300 |
2200 |
2000 |
900 |
请根据上表提供的信息,回答下列问题:
(1) 如果学校准备招聘“高级教师”和“中级教师”共40名,(其他员工人数不变)。其中高级教师至少要招聘13人,而且学校对高级,中级教师的月支付工资不超过83000元,按学校要求,对高级、中级教师有几种招聘方案?
(2) (1)中的那种方案对学校所支付的月工资最少?并说明理由。
(3) 在学校所支付的月工资最少时,将上表补充完整,并求所有员工月工资的中位数和众数。
21.(10分)如图,直角坐标系中,点A的坐标为(1.0),以线段OA为边在第四象限内作等边三角形AOB,点C为线段OA延长线上一动点,连接BC,以线段BC为边在第四象限内作等边三角形CBD,直线DA交y轴于点E。
(1)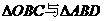 全等吗?判断并证明你的结论:
全等吗?判断并证明你的结论:
(2)随着点C的位置的变化,点E的位置是否会发生变化?若没有变化,求出点E的坐标:若有变化,请说明理由。
20.(8分)如图某幢大楼顶部有广告牌CD,张老师目高MA为1.60米,他站立在离大楼45米的A处测得大楼顶端点D的仰角为 :接着他向大楼前进14米站在点B处,测得广告牌顶端点C的仰角为
:接着他向大楼前进14米站在点B处,测得广告牌顶端点C的仰角为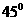 。(计算结果保留一位小数,
。(计算结果保留一位小数,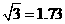 )
)
(1)求这幢大楼的高DH:
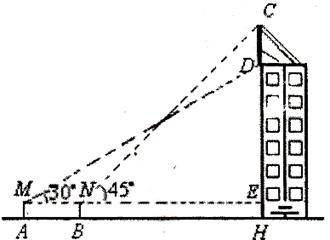 (2)求这块广告牌CD的高度。
(2)求这块广告牌CD的高度。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com