
题目列表(包括答案和解析)
1.2 因分式解法,直接开平方法(2)同步练习
考标要求:
1 体会因式分解法适用于解一边为0,另一边可分解为两个一次因式的乘积的一元二次方程;
2 会用因式分解法解某些一元二次方程。
重点:用因式分解法解一元二次方程。
难点:用因式分解把一元二次方程化为左边是两个一次二项式相乘右边是零的形式。
一 填空题(每小题5分,共25分)
1 解方程(2+x)(x-3)=0,就相当于解方程( )
A 2+x=0 , B x-3=0 C 2+x=0 且 x-3=0 ,D 2+x=0或x-3=0
2 用因式分解法解一元二次方程的思路是降次,下面是甲、乙两位同学解方程的过程:
(1)解方程: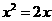 ,小明的解法是:解:两边同除以x得:x=2;
,小明的解法是:解:两边同除以x得:x=2;
(2) 解方程: (x-1)(x-2)=2,小亮的解法是:解:x-1=1,x-2=2 或者x-1=2,x-2=1,或者,x-1= -1,x-2= -2,或者x-1= -2,x-2= -1∴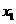 =2,
=2,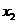 =4,
=4,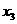 =3,
=3,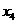 =0
=0
其中正确的是( )
A 小明 B 小亮 C 都正确 D 都不正确
3 下面方程不适合用因式分解法求解的是( )
A 2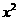 -32=0, B 2( 2x-3) -
-32=0, B 2( 2x-3) - 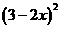 =0 ,
=0 ,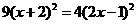 ,D
,D 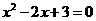
4 方程2 x (x-3) = 5 (x-3)的根是( )
A x=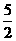 , B x=3 C
, B x=3 C 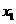 =
=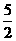 ,
, 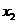 =3 D x=
=3 D x=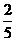
5 定义一种运算“※”,其规则为:a※b=(a+1) (b+1),根据这个规则,方程x※(x+1)=0的解是( )
A
x=0 B x= -1 C 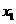 =0,
=0, 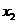 =-1,
D
=-1,
D 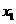 = -1
= -1 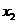 = - 2
= - 2
二 填空题(每小题5分,共25分)
6 方程(1+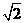 )
)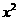 -(1-
-(1-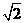 )x = 0解是
)x = 0解是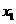 =_____,
=_____,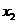 =__________
=__________
7当x=__________时,分式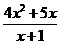 值为零。
值为零。
8 若代数式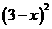 与代数式4(x-3)的值相等,则x=_________________
与代数式4(x-3)的值相等,则x=_________________
9 已知方程(x-4)(x-9)=0的解是等腰三角形的两边长,则这个等腰三角形的周长=_______.
10 如果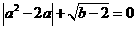 ,则关于x的一元二次方程a
,则关于x的一元二次方程a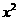 +bx=0的解是_________
+bx=0的解是_________
三 解答题(每小题10分,共50分)
11 解方程
(1)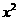 +2x+1=0 (2)
4
+2x+1=0 (2)
4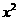 -12x+9=0
-12x+9=0
(3) 25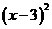 =9
=9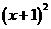 (4) 7x (2x-3)=4 (3-2x)
(4) 7x (2x-3)=4 (3-2x)
12 解方程 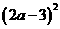 =(a-2)(3a-4)
=(a-2)(3a-4)
13已 知k是关于x的方程4k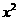 -8x-k=0的一个根,求k的值。?
-8x-k=0的一个根,求k的值。?
14 解方程 :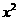 -2
-2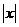 +1=0
+1=0
15 对于向上抛的物体,在没有空气阻力的情况下,有如下关系:h=vt -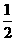 g
g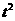 ,其中h是上升到高度,v是初速度,g是重力加速度,(为方便起见,本题中g取10米/
,其中h是上升到高度,v是初速度,g是重力加速度,(为方便起见,本题中g取10米/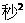 ),t是抛出后所经过的时间。
),t是抛出后所经过的时间。
如果将一物体以每秒25米的初速向上抛,物体多少秒后落到地面
1.2 因分式解法,直接开平方法(1) 同步练习
(时量:45分钟,满分:100分)
考标要求:
1知道解一元二次方程的基本思路是“降次”化为一元一次方程;
2会用因式分解法和直接开平方法解形如: 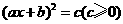 的方程
的方程
重点:用因式分解法和直接开平方法解形如: 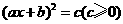 的方程
的方程
难点:通过因式分解或直接开平方把一元二次方程降次。
一 选择题(每小题 5分,共25分)
1 关于x的方程 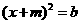 能用直接开平方法求解的条件是( )
能用直接开平方法求解的条件是( )
A m为任意实数,b>0 B m为任意实数,b≥0 C m>0,b>0 D m<0,b>0
2 一元二次方程 的解是( )
的解是( )
A 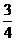 ,
B -
,
B - 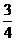 ,C
,C 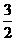 D ±
D ±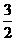
3解一元二次方程的基本思路是“降次”,把方程:x(x+4)= -4以化为下面方程求解正确的是( )
A x=1 或x+4= -4 B x=-1或x+4= 4 C x+2=0 D 以上都不对
4 2.方程3x2+9=0的根为( ).
A.3 B.-3 C.±3 D.无实数根
5 把方程4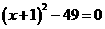 化为两个一元一次方程求解正确的是( )
化为两个一元一次方程求解正确的是( )
A 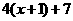 =0或
=0或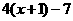 =0 B
=0 B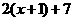 =0或
=0或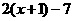 =0
=0
C 4x+1+7=0或4x+1-7=0 D2x+1+7=0或2x+1-7=0
二 填空题(每小题5分,共25分)
6 解方程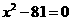 时,我们把它化为
时,我们把它化为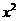 =81,然后得到
=81,然后得到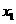 =9,
=9, 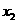 = -9,这样做的道理是根据________的定义
= -9,这样做的道理是根据________的定义
7 若代数式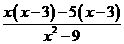 的值为0 ,则代数式x-3=_________;
的值为0 ,则代数式x-3=_________;
8 方程5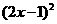 =80的解是_________
=80的解是_________
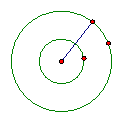 9 如图,已知大圆的半径为5cm,圆环的面积为9
9 如图,已知大圆的半径为5cm,圆环的面积为9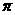
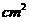 ,则小圆的半径为______cm
,则小圆的半径为______cm
10 某工厂引进了新技术,使产品的成本两年内以每件2500元降到1600
元,则平均每年降低的百分数是_______.
三 解答题 ( 每小题10分,共50分)
11 解下列方程:
(1)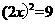 ;
(2)
;
(2) 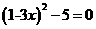
(3) 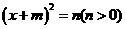 (4)
(4) 
12 已知x、y满足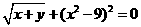 ,求xy的值。
,求xy的值。
13市政府决心加大廉租房建设的力度,计划2年内将人均住房面积由现在的10m2提高到14.4  ,求每年人均住房面积增长率。
,求每年人均住房面积增长率。
14 已知等腰直角三角形的斜边长为32cm,求直角边的长。
15 小明“五一”节去公园游玩,看到一个可爱的小朋友,问:“小朋友,你今年几岁了?”小朋友的爸爸说:“他今天年龄的平方恰好等于他去年的年龄的4倍”,小明想了想就知道了这位小朋友今年几岁了,你知道吗?
四 拓展探究(不计总分)
形如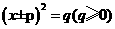 的方程可以用直接开平方法求解,有些方程可以转化为这种形式来解,如:
的方程可以用直接开平方法求解,有些方程可以转化为这种形式来解,如: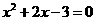 ,可以写成:
,可以写成: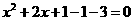 ,
,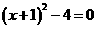 ,再用直接开平方法或者因式分解法解,你能不能将下列方程先化为
,再用直接开平方法或者因式分解法解,你能不能将下列方程先化为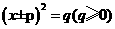 的形式,再求出未知数的值?
的形式,再求出未知数的值?
(1)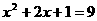 ;
;
(2)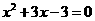
24.2相似三角形的判定
第1题. 如图,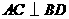 ,垂足为
,垂足为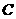 ,过
,过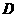 点作
点作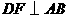 ,垂足为
,垂足为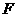 ,交
,交 于
于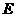 点.请找出图中所有的相似三角形,并说明理由.
点.请找出图中所有的相似三角形,并说明理由.

答案:解:(1)因为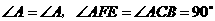
所以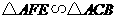 .
.
(2)因为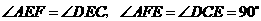 ,
,
所以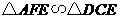 .
.
所以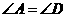 .
.
(3)因为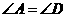 ,
,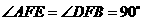 ,
,
所以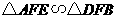 .
.
(4)因为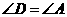 ,
,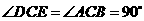 ,
,
所以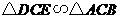 .
.
(5)因为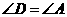 ,
,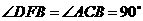 ,
,
所以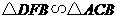 .
.
(6)因为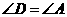 ,
,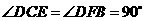 ,
,
所以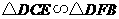 .
.
知识点:三角形相似的条件 试题类型:运算题 试题难度:容易 考查目标:基本技能
第2题. 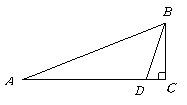 如图,一艘军舰从点
如图,一艘军舰从点 向位于正东方向的
向位于正东方向的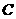 岛航行,在点
岛航行,在点 处测得
处测得 岛在其北偏东
岛在其北偏东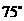 ,航行75n mile到达点
,航行75n mile到达点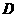 处,测得
处,测得 岛在其北偏东
岛在其北偏东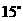 ,继续航行5n mile到达
,继续航行5n mile到达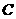 岛,此时接到通知,要求这艘军舰在半小时内赶到正北方向的
岛,此时接到通知,要求这艘军舰在半小时内赶到正北方向的 岛执行任务,则这艘军舰航行速度至少为多少时才能按时赶到
岛执行任务,则这艘军舰航行速度至少为多少时才能按时赶到 岛?
岛?
答案:解:根据题意,可得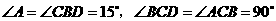 .
.
所以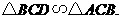
由相似三角形对应边成比例,得
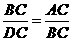 ,即
,即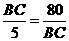 .
.
所以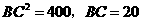 .
.
要求军舰在半小时内赶到正北方向的 岛执行任务,因此航行速度至少是
岛执行任务,因此航行速度至少是
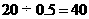 (n
mile/h)
(n
mile/h)
知识点:三角形相似的条件 试题类型:应用题 试题难度:中等 考查目标:双基简单应用
第3题. 如图,点 分别在
分别在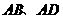 上,
上,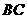 与
与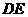 相交于一点
相交于一点 ,若
,若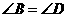 ,
,
 则图中相似三角形有几对?分别写出来说明理由.
则图中相似三角形有几对?分别写出来说明理由.
答案:2对 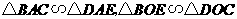 .理由略
.理由略
知识点:三角形相似的条件 试题类型:运算题 试题难度:容易 考查目标:基本技能
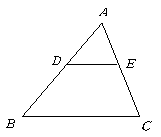
第4题. 如图,已知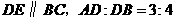 ,若
,若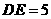 cm,求
cm,求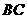 的长.
的长.
答案: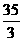 cm
cm
知识点:三角形相似的条件 试题类型:运算题 试题难度:中等 考查目标:基本技能
第5题. 如图,已知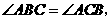 若
若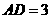 cm,
cm,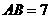 cm,试求
cm,试求 的长.
的长.

答案: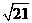 cm
cm
知识点:三角形相似的条件 试题类型:运算题 试题难度:中等 考查目标:基本技能
第6题. 如图, 为
为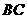 的中点,求
的中点,求 的周长.
的周长.
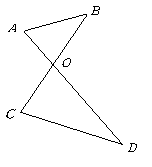
答案:解:由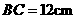 ,
, 为
为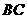 的中点,得
的中点,得
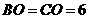 cm.
cm.
由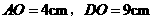 ,得
,得
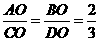 .
.
因为两边对应成比例且夹角相等的两个三角形相似,
所以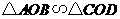 .
.
由相似三角形对应边成比例,得
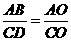 ,即
,即 .
.
所以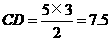 (cm).
(cm).
因此, 的周长是
的周长是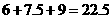 (cm).
(cm).
知识点:三角形相似的条件 试题类型:运算题 试题难度:中等 考查目标:基本技能
第7题. 已知 的三条边长之比为
的三条边长之比为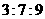 ,与其相似的另一个
,与其相似的另一个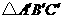 最大的边长为18cm,则
最大的边长为18cm,则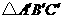 最小的边长为 cm,周长为 cm.
最小的边长为 cm,周长为 cm.
答案:6 38
知识点:三角形相似的条件 试题类型:填空题 试题难度:容易 考查目标:基本技能
第8题. 如图,在 中,点
中,点 分别在边
分别在边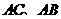 上,且
上,且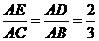 ,若
,若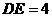 cm,则
cm,则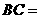 cm.
cm.
答案:6
知识点:三角形相似的条件 试题类型:填空题 试题难度:中等 考查目标:基本技能
第9题.  如图,点
如图,点 分别为边
分别为边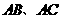 的三等分点(即:
的三等分点(即: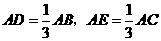 ),若
),若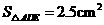 ,求
,求 的大小.
的大小.
答案: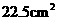
知识点:三角形相似的条件 试题类型:运算题 试题难度:中等 考查目标:双基简单应用
第10题. 如图,在 中,
中,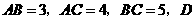 是
是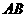 上的一点,
上的一点,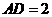 ,在
,在 上是否存在一点
上是否存在一点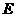 ,使
,使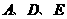 三点组成的三角形与
三点组成的三角形与 相似?如果存在,请求出
相似?如果存在,请求出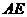 的长;如果不存在,请说明理由.
的长;如果不存在,请说明理由.
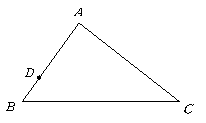
答案:解:存在.
因为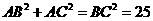 ,
,
所以 是直角三角形,
是直角三角形,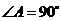 .
.
设所求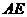 的长为
的长为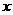 ,
,
在 与
与 中,
中,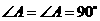 ,
,
(1)若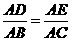 ,则
,则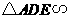
 .
.
此时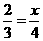 .
.
解得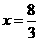 .
.
(2)若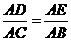 ,则
,则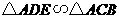 .
.
此时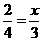 .
.
解得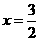 .
.
所以,当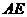 取
取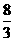 或
或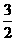 时,
时,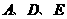 三点组成的三角形与
三点组成的三角形与 相似.
相似.
知识点:三角形相似的条件 试题类型:运算题 试题难度:中等 考查目标:双基简单应用
第11题. 如图,下列条件中不能判定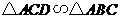 的是( )
的是( )
(A)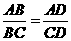 (B)
(B)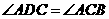
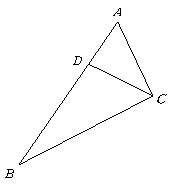 (C)
(C)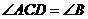 (D)
(D)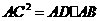
答案:(A)
知识点:三角形相似的条件 试题类型:选择题 试题难度:中等 考查目标:基本技能
第12题. 已知:如图,点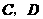 在线段
在线段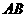 上,
上,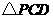 是等边三角形.(1)当
是等边三角形.(1)当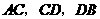 满足怎样的关系式时
满足怎样的关系式时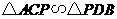 ;(2)当
;(2)当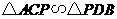 时,求
时,求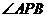 的度数.
的度数.
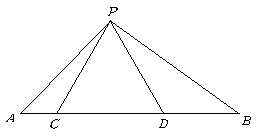
答案:解:(1)当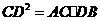 时,
时,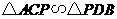 ;
;
(2)当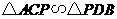 时,
时,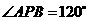 .
.
知识点:三角形相似的条件 试题类型:运算题 试题难度:中等 考查目标:数学思考
第13题. 在 和
和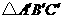 中,
中,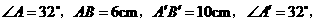
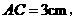
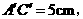 则
则 与
与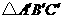 是否相似? (填“是”或“不是”).
是否相似? (填“是”或“不是”).
答案:是
知识点:三角形相似的条件 试题类型:填空题 试题难度:容易 考查目标:基本技能
第14题. 下列四组图形中不一定相似的是 .
A.有一个角等于 的两个等腰三角形
的两个等腰三角形
B.有一个角为 的两个直角三角形
的两个直角三角形
C.直角三角形被斜边上的高分成的两个直角三角形
D.有一个角是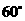 的两个等腰三角形
的两个等腰三角形
答案:A
知识点:三角形相似的条件 试题类型:选择题 试题难度:容易 考查目标:基本技能
第15题. 能判定 与
与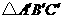 相似的条件是 .
相似的条件是 .
A.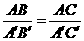 B.
B.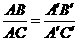 ,且
,且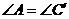
C.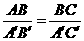 且
且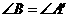 D.
D.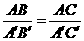 ,且
,且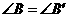
答案:C
知识点:三角形相似的条件 试题类型:选择题 试题难度:容易 考查目标:基本技能
第16题. 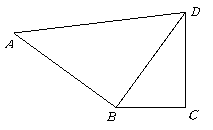 已知:如图,
已知:如图, ,当
,当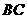 为多少时,图中的两个三角形相似.
为多少时,图中的两个三角形相似.
答案: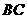 为3.6或4.8
为3.6或4.8
知识点:三角形相似的条件 试题类型:运算题 试题难度:中等 考查目标:双基简单应用
第17题. 如图,线段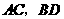 相交于点
相交于点 ,要使
,要使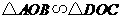 ,已具备条件 ,还需要补充的条件是 ,或 或 .
,已具备条件 ,还需要补充的条件是 ,或 或 .
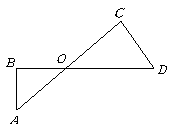
答案:
知识点:三角形相似的条件 试题类型:填空题 试题难度:容易 考查目标:基本技能
第18题. 如图,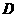 为
为 的边
的边 上的一点,连接
上的一点,连接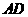 ,要使
,要使 ,应具备下列条件中的( )
,应具备下列条件中的( )
A.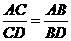 B.
B.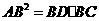
 C.
C.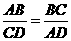 D.
D.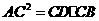
答案:B
知识点:三角形相似的条件 试题类型:选择题 试题难度:容易 考查目标:基本技能
第19题. 如图,已知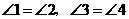 .
.
(1)图中有哪几对相似三角形?把它们写出来;
(2)证明你所写出的结论.

答案:(1)解:图中的相似三角形有三对,它们分别是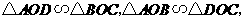
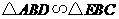
(2)证明: ,
,
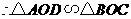 ,
,
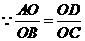 ,即
,即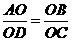 ,
,
又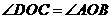 ,
,
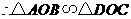
又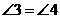 ,
,
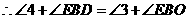
即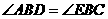
 .
.
知识点:三角形相似的条件 试题类型:运算题 试题难度:中等 考查目标:双基简单应用
第20题. 如图12,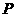 是
是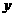 轴上一动点,是否存在平行于
轴上一动点,是否存在平行于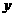 轴的直线
轴的直线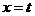 ,使它与直线
,使它与直线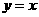 和
和
直线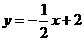 分别交于点
分别交于点 (
(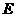 在
在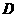 的上方),且
的上方),且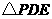 为等腰直角三角
为等腰直角三角
形.若存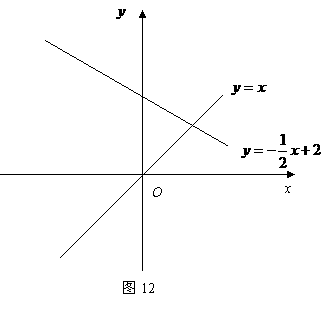 在,求
在,求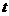 的值及点
的值及点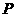 的坐标;若不存在,请说明原因.
的坐标;若不存在,请说明原因.
答案:解:存在.
方法一:当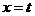 时,
时,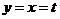 ;当
;当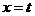 时,
时, .
.
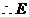 点坐标为
点坐标为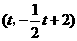 ,
,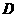 点坐标为
点坐标为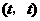 .
.
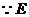 在
在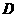 的上方,
的上方,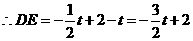 ,且
,且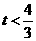 . 3分
. 3分
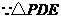 为等腰直角三角形,
为等腰直角三角形,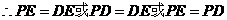 .
.
若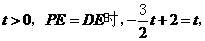
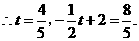
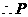 点坐标为
点坐标为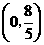 .
.
若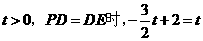 ,
,
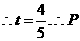 点坐标为
点坐标为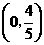 .
.
若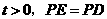 时,即
时,即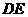 为斜边,
为斜边,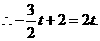
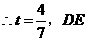 的中点坐标为
的中点坐标为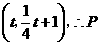 点坐标为
点坐标为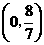 .
.
若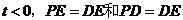 时,由已知得
时,由已知得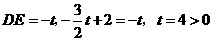
(不符合题意,舍去),
此时直线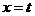 不存在.
不存在.
若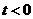 ,
,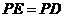 时,即
时,即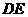 为斜边,由已知得
为斜边,由已知得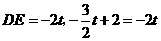 ,
,
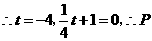 点坐标为
点坐标为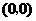 .
.
综上所述:当 时,
时,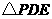 为等腰直角三角形,此时P点坐标为
为等腰直角三角形,此时P点坐标为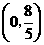 或
或
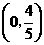 ;当
;当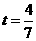 时,
时,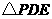 为等腰直角三角形,此时P点坐标为
为等腰直角三角形,此时P点坐标为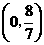 ;
;
当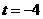 时,
时,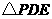 为等腰直角三角形,此时P点坐标为
为等腰直角三角形,此时P点坐标为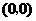 .
.
方法二:设直线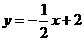 交
交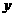 轴于点
轴于点 ,交直线
,交直线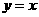 于点
于点 ,过
,过 点作
点作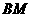
垂直于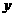 轴,垂足为
轴,垂足为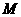 ,交
,交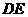 于点
于点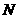 .
.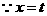 平行于
平行于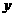 轴,
轴,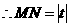 .
.

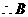 点坐标为
点坐标为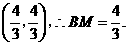 2分
2分
当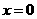 时,
时,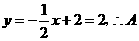 点坐标为
点坐标为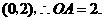 3分
3分
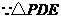 为等腰直角三角形,
为等腰直角三角形,
如图4,若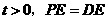 和
和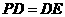 时,
时,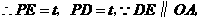
 .
.
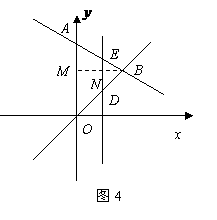
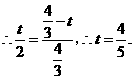
当 时,
时,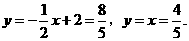
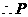 点坐标为
点坐标为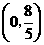 或
或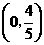 .
.
若 时,即
时,即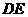 为斜边,
为斜边,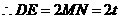 .
.
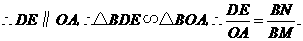

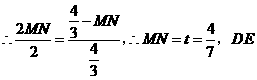 中点的纵坐标为
中点的纵坐标为 点坐标
点坐标
为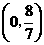
如图5,若 时,
时,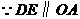 ,
,
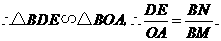
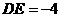 (不符合题意,舍去),此时直线
(不符合题意,舍去),此时直线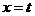 存在. 10分
存在. 10分
若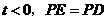 时,即
时,即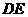 为斜边,
为斜边,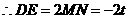
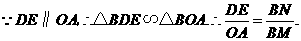
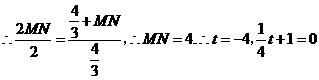
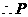 点坐标为(0,0).
点坐标为(0,0).
综上述所述:当 时,
时,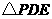 为等腰直角三角形,此时
为等腰直角三角形,此时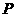 点坐标为
点坐标为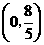 或
或
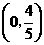 ;当
;当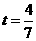 时,
时,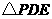 为等腰直角三角形,此时
为等腰直角三角形,此时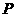 点坐标为
点坐标为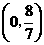 ;当
;当
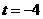 时,
时,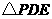 为等腰直角三角形,此时
为等腰直角三角形,此时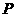 点坐标为(0,0).
点坐标为(0,0).
知识点:6 探索三角形相似的条件 综合知识点 试题类型:合情推理题 试题难度:较难 考查目标:数学思考
第21题.  如图,
如图,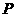 是Rt
是Rt 的斜边
的斜边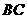 上异于
上异于 、
、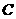 的一点,过
的一点,过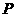
点作直线截 ,使截得的三角形与
,使截得的三角形与 相似,满足这样条件
相似,满足这样条件
的直线共有( )条
A.1 B.2 C.3 D.4
答案:C
知识点:三角形相似的条件 试题类型:选择题 试题难度:中等 考查目标:数学思考
第22题. .如图5,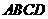 是平行四边形,则图中与
是平行四边形,则图中与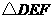 相似的三角形
相似的三角形
 共有( )
共有( )
(A)1个 (B)2分
(C)3个 (D)4个
答案:B
知识点:三角形相似的条件 试题类型:选择题 试题难度:容易 考查目标:基础知识
第23题. 如图,梯形ABCD中,AD//BC,BD为对角线,中位线EF交BD于O点,
若FO-EO=3,则BC-AD等于
A.4 B.6 C.8 D.10

答案:B
试题号:13094 知识点:三角形相似的条件 试题类型:选择题 试题难度:中等 考查目标:双基简单应用 录入时间:2005-9-15
(13134)第24题. 如图,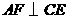 ,垂足为点
,垂足为点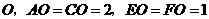 .
.
(1)求证:点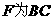 的中点;
的中点;
 (2)求四边形
(2)求四边形 的面积.
的面积.
答案:解:(1)连结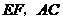


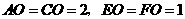 ,
,
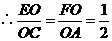 .
.
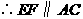 .
.
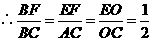 .
.
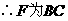 的中点.
的中点.
(2)由(1)知,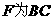 的中点.
的中点.
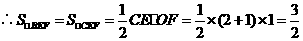 .
.
又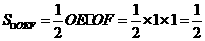 ,
,

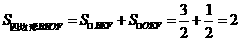
知识点:三角形相似的条件 试题类型:运算题 试题难度:中等 考查目标:双基简单应用
第25题. 小胖和小瘦去公园玩标准的跷跷板游戏,两同学越玩越开心,小胖对小瘦说:“真可惜!
我只能将你最高翘到1米高,如果我俩各边的跷跷板都再伸长相同的一段长度,那么我
就能翘到1米25,甚至更高!”
(1)你认为小胖的话对吗?请你作图分析说明;
(2)你能否找出将小瘦翘到1米25高的方法?试说明.
 解:
解:
答案:解:(1)小胖的话不对.
小胖说“真可惜!我现在只能将你最高翘到1
米高”,情形如图(1)所示,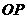 是标准跷跷
是标准跷跷
板支架的高度, 是跷跷板一端能翘到的最
是跷跷板一端能翘到的最
高高度1米,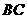 是地面.
是地面.
又 此跷跷板是标准跷跷板,
此跷跷板是标准跷跷板,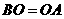 ,
,
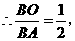 而
而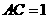 米,得
米,得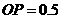 米.
米.
 若将两端同时都再伸长相同的长度,假设为
若将两端同时都再伸长相同的长度,假设为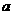 米
米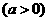 .
.
如图(2)所示,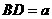 米,
米,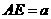 米
米
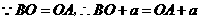 ,即
,即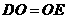 .
.
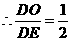 ,同理可得
,同理可得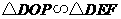 .
.
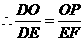 ,由
,由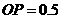 米,得
米,得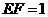 米.
米.

综上所述,跷跷板两边同时都再伸长相同的一段长度,
跷跷板能翘到的最高高度始终为支架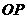 高度的两倍,
高度的两倍,
所以不可能翘得更高.
(2)方案一:如图(3)所示,保持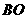 长度不变.将
长度不变.将
 延长一半至
延长一半至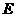 ,即只将小瘦一边伸长一半.
,即只将小瘦一边伸长一半.
使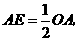 则
则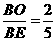 .
.
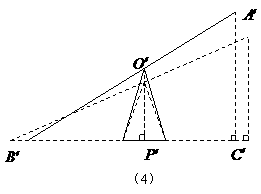 由
由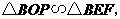 得
得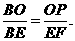
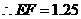 米.
米.
方案二:如图(4)所示,只将支架升高0.125米.
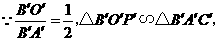
又 米.
米.
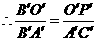 .
.
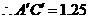 米.
米.
(注:其它方案正确,可参照上述方案评分!)
知识点:6 探索三角形相似的条件 综合知识点 试题类型:运算题 试题难度:中等 考查目标:双基简单应用
第26题. 在△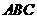 中,
中,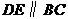 ,
,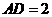 ,
,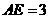 ,
,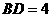 ,则
,则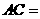 .
.
答案:9
知识点:6 探索三角形相似的条件 综合知识点 试题类型:填空题 试题难度:容易 考查目标:基础知识
24.4相似多边形的性质同步练习
第1题. 如果一个矩形和它的一半矩形相似,那么大矩形与小矩形的相似比是( )
A.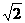 :1 B.
:1 B. C.2:1 D.1:2
C.2:1 D.1:2
答案:A
第2题. 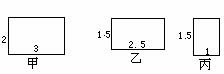 如图中,有三个矩形,其中相似的是( )
如图中,有三个矩形,其中相似的是( )
A.甲和乙 B.甲和丙
C.乙和丙 D.没有相似的矩形
答案:B
第3题. 下列各组图形中,肯定是相似形的是( )
A.两个腰长不相等的等腰三角形
B.两个半径不等的圆
C.两个面积不相等的平行四边形
D.两个面积不相等的菱形
答案:B
第4题. 在四边形ABCD与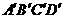 中,∠A=∠
中,∠A=∠ ,∠B=∠
,∠B=∠ ,∠C=∠
,∠C=∠ ,∠D=∠
,∠D=∠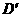 ,且
,且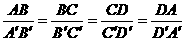 =
=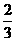 ,则四边形 ∽四边形 ,且四边形ABCD与
,则四边形 ∽四边形 ,且四边形ABCD与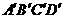 的相似比是 , 四边形ABCD与
的相似比是 , 四边形ABCD与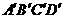 的面积比是 .
的面积比是 .
答案:ABCD,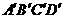 ,
,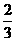 ,
,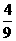
第5题. 已知两个多边形相似,它们的面积的比为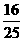 ,若其中一个周长为28,则另一个多边形的周长为 .
,若其中一个周长为28,则另一个多边形的周长为 .
答案:35或22.4
第6题. 顶角都是20°的两个等腰三角形是否相似?各有一个20°角的两个直角三角形是否相似?
答案:相似,相似
第7题. 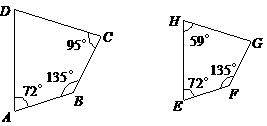 图中的两个多边形相似吗?说说你判断的理由.
图中的两个多边形相似吗?说说你判断的理由.
答案:不相似,∠D=360°-135°-95°-72°=58°,而∠E=360°-135°-95°-59°=71°,不可能有"对应角相等".
第8题. 已知下图中的两个四边形相似,找出图中的成比例线段,并用比例式表示.
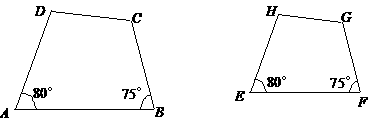
答案:
第9题. 用一个放大镜看一个四边形ABCD,该四边形的边长放大10倍后,下列结论正确的是( )
A.∠A是原来的10倍 B.周长是原来的10倍
C.面积是原来的10倍 D.四边形的形状发生了改变
答案:B
第10题. 两个多边形相似,面积的比是1∶4,一个多边形的周长为16,则另一个多边形的周长为 .
答案:8或32
第11题. 两个多边形相似,相似比是3:5,则其周长之比是 ,面积之比是 .
答案:3∶5,9∶25
第12题. 请将下图中的相似图形的序号写出来 .
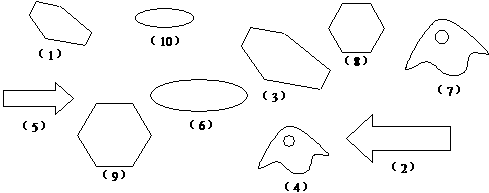
答案:(1)和(3);(2)和(5);(4)和(7);(8)和(9);(6)和(10)
第13题. 等腰三角形ABC的腰长是等腰三角形DEF的腰长的2倍,讨论这两个三角形什么时候相似.
答案:顶角相等或有一个底角相等时都相似,△ABC的底边是△DEF底边的2倍时也相似.
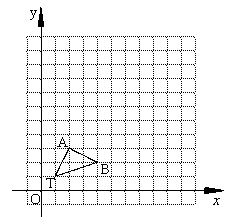
25.如图,在12×12的正方形网格中,△TAB 的顶点坐标分别为T(1,1)、A(2,3)、
B(4,2)。
(1)以点T(1,1)为位似中心,按比例尺(TA′∶TA)3∶1在位似中心的同侧将△TAB放大为△TA′B′,放大后点A、B的对应点分别为A′、B′.画出△TA′B′,并写出点A′、B′的坐标;
(2)在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标。
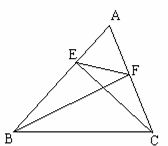
24.如图,已知△ABC中CE⊥AB于E,BF⊥AC于F,
求证:⑴ΔABF∽ΔACE;⑵ΔAEF∽ΔACB。
23.如图,在Rt△ABC中,∠B=900,AB=BE=EF=FC。求证:△AEF∽△CEA。

22.如图,∠ACB=∠ADC=900,AC=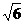 ,AD=2。问当AB的长为多少时,这两个直角三角形相似?
,AD=2。问当AB的长为多少时,这两个直角三角形相似?

21.如图,在△ABC中,矩形DEFG,G、F在BC上,D、E分别在AB、AC上,AH⊥BC交DE于M,DG∶DE=1∶2,BC=12 cm,AH=8 cm,求矩形的各边长。

20.如图,已知菱形AMNP内接于△ABC,M、N、P分别在AB、BC、AC上,如果AB=21 cm,CA=15 cm,求菱形AMNP的周长。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com