
题目列表(包括答案和解析)
3.如图在Rt△ABC中,∠C=90°∠B=30°,AB=2,
 则AC= 。
则AC= 。
2.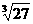 = 。
= 。
1. 在实数
在实数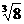 ,
,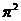 ,
, 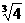 ,
,
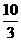 ,
, 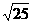 中是
无理数 。
中是
无理数 。
例6 在栽植农作物时,一个很重要的问题是“合理密植”.如图是栽植一种蔬菜时的两种方法,A、B、C、D四珠顺次连结成为一个菱形,且AB=BD;A′、B′、C′、D′四株连结成一个正方形,这两种图形的面积为四株作物所占的面积,两行作物间的距离为行距;一行中相邻两株作物的距离为株距;设这两种蔬菜充分生长后,每株在地面上的影子近似成一个圆面(相邻两圆如图相切),其中阴影部分的面积表示生长后空隙地面积.在株距都为a,其他客观因素也相同的条件下,请从栽植的行距,蔬菜所占的面积,充分生长后空隙地面积三个方面比较两种栽植方法.哪种方法能更充分地利用土地.
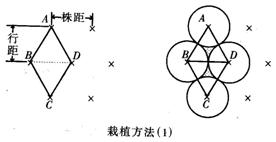

分析:本题立意很新,要合理密植,充分利用土地,只需分别计算并比较两种方案的行距、阴影面积以及S和S.对应值小的即为合理密植.
解 连结AC交BD于点O.在菱形ABCD中,有AB=AD,AC⊥BD,BO=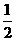 BD.
BD.
∵AB=BD=a,∴BO=OD=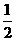 a.
a.
在Rt△AOD中,AO=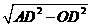 =
=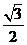 a.
a.
∴S菱形ABCD=2×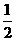 BD·AO=
BD·AO=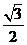 a2,
a2,
S正方形A`B`C`D`=a2.
设方法(1)中空隙地面积为S1,方法(2)中空隙地面积为S2.
则S1=S菱形ABCD-S☉A=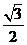 a2-
a2-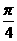 a2,
a2,
S2=S正方形A`B`C`D`-S☉A`=a2-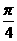 a2.
a2.
∵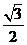 <1,
<1,
∴AO<A′B′,
S菱形ABCD<S正方形A`B`C`D`,S1<S2.
∴栽植方法(1)比栽植方法(2)能更充分地利用土地.
例5 如图,矩形ABCD的长与宽分别是2cm和1cm,AB在直线L上,依次为B、C′、D″,依次为B、C′、D″为中心将矩形ABCD按顺时针方向旋转90°.这样点A走过的曲线依次为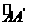 、
、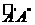 、
、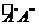 ,其中
,其中 交CD于点P.
交CD于点P.
(1)求矩形A′BC′D′的对角线A′C′的长;
(2)求 的长;
的长;
(3)求图中 部分的面积S;
(4)求图中 部分的面积T.(2005年吉林省中考题)
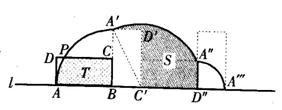
分析 (1)要求A′C′,因长宽分别为2和1,利用勾股定理即可;(2)要求 ,因
,因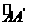 所对圆心角为∠ABA′=90°,半径AB=2,利用弧长公式即可;(3)因△A′C′D′≌△A″C′D″,故S=S扇形A`C``A``;(4)连PB,则PB=AB=2,又BC=1,故∠PBC=60°,∠ABP=30°,欲求T,由“T=S扇形ABP+S△BCP”即可.
所对圆心角为∠ABA′=90°,半径AB=2,利用弧长公式即可;(3)因△A′C′D′≌△A″C′D″,故S=S扇形A`C``A``;(4)连PB,则PB=AB=2,又BC=1,故∠PBC=60°,∠ABP=30°,欲求T,由“T=S扇形ABP+S△BCP”即可.
解答 (1)A′C′=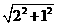 =
=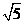 (cm).
(cm).
(2)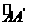 =
=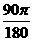 ×2=
×2=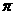 (cm).
(cm).
(3)S=S扇形A`CA``=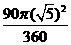 =
=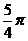 (cm)
(cm)
(4)连结BP,在Rt△BCP中,BC=1,BP=2,
∴∠BPC=30°,CP=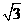 ,∴∠ABP=30°,
,∴∠ABP=30°,
∴T=S扇形ABP+S△PBC=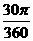 ×22+
×22+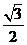 =(
=( +
+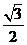 )cm2.
)cm2.
例4 如图,半圆A和半圆B均与y轴相切于点O,其直径CD、EF均和x轴垂直,以O为顶点的两条抛物线分别经过C、E和D、F,则图中阴影部分的面积是_________.(2005年河南省中考题)

分析 由题意知,图中两半圆和两抛物线组成的图形关于y轴对称,故y轴左侧阴影部分面积等于半圆B中的空白面积,所以所求阴影部分面积为半圆B的面积,即S阴=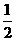
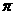 ·12=
·12=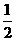
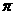 .
.
解答: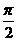 .
.
例3 图中的虚线网格我们称之为正三角形网格,它的每个小三角形都是边长为1个单位长度的正三角形,这样的三角形称为单位正三角形.
(1)直接写出单位正三角形的高与面积;
(2)图1中的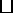 ABCD含有多少个单位正三角形?ABCD的面积是多少?
ABCD含有多少个单位正三角形?ABCD的面积是多少?
(3)求出图1中线段AC的长(可作辅助线);
(4)求出图2中四边形EFGH的面积.(2005年吉林省中考题)
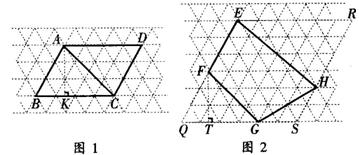

分析 (1)由正三角形边角关系来求;(2)仔细观察图1便可找到答案;(3)考虑到图1中AB=3,BC=4,∠B=60°,可作△ABC的高AK,构造直角三角形,再利用解直角三角形知识即可求得;(4)可利用网格构造特殊格点图形,再由求补法计算四边形EFGH面积.
解:(1)单位正三角形的角为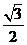 ,面积为
,面积为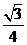 ,
,
(2)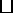 ABCD含有24个单位正三角形,故其面积为24×
ABCD含有24个单位正三角形,故其面积为24×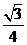 =6
=6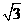 .
.
(3)如图1,过A作AK⊥BC于K,在Rt△ACK中,AK=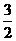
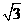 ,KC=
,KC=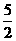 .
.
∴AC=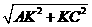 =
=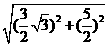 =
=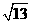 .
.
(4)如图3,构造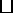 EQSR,过F作FT⊥QG于T,则S△FQG=
EQSR,过F作FT⊥QG于T,则S△FQG=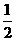 FT·QG=
FT·QG=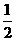 ×
×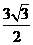 ×4=3
×4=3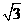 .
.
同理可求
S△GSH=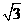 ,S△EHR=6
,S△EHR=6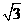 ,S
,S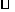 EQSR=18
EQSR=18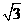 .
.
∴S四边形EFGH=
S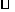 EQSR -S△FQG-S△GSH-S△EHR=18
EQSR -S△FQG-S△GSH-S△EHR=18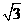 -3
-3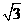 -
-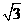 -6
-6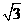 =8
=8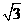 .
.
例2 在一块长16m,宽12m的矩形荒地上,要建造一个花园,要求花园所占面积为荒地面积的一半.下面分别是小明和小颖的设计方案.
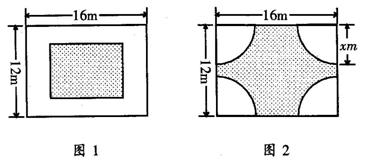
小明的设计方案:如图1,其中花园四周小路的宽度相等,经过解方程,我得到路的宽为2m或12m.
小颖的设计方案:如图2,其中花园中每个角上的扇形都相同.
(1)你认为小明的结果对吗?请说明理由.
(2)请你帮助小颖求出图中的x(精确到0.1m)
(3)你还有其它的设计方案吗?请在右边的矩形中画出你的设计草图,并加以说明.(2004年新疆建设兵团中考题)
分析 (1)由小明的设计知,小路的宽应小于矩形荒地宽的一半,由此判断即可;(2)可由“花园面积为矩形面积一半”列方程求x;(3)可由图形对称性来设计.
解 (1)小明的结果不对.
设小路宽xm,则得方程
(16-2x)(12-2x)=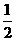 ×16×12
×16×12
解得:x1=2,x2=12.而荒地的宽为12m,若小路宽为12m,不符合实际情况,故x2=12m不合题意.
(2)由题意,4×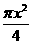 =
=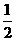 ×16×12
×16×12
x2=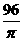 ,x≈5.5m.
,x≈5.5m.
(3)方案有多种,下面提供5种供参考:
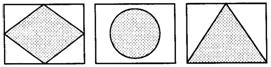
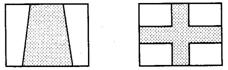
例1 宏远广告公司要为某企业的一种产品设计商标图案,给出了如下几种初步方案,供继续设计选用(设图中圆的半径均为r).
(1)如图1,分别以线段O1O2的两个端点为圆心,以这条线段的长为半径作出两个互相交错的圆的图案,试求两圆相交部分的面积.
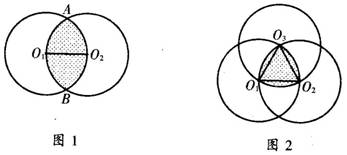
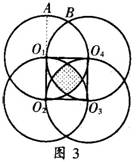
(2)如图2,分别以等边△O1O2O3的三个顶点为圆心,以其边长为半径,作出三个两两相交的相同的圆,这时,这三个圆相交部分的面积又是多少呢?
(3)如图3,分别以正方形O1O2O3O4的四个顶点为圆心,以其边长为半径作四个相同的圆,则这四个圆的相交部分的面积又是多少呢?(2005年黄冈市中考题)
分析 (1)利用“S阴=S菱形AO1BO2=4S弓形”即可;(2)利用“S阴=S△O1O2O3+3S弓”即可;(3)直接求解比较困难,可利用求补法,即“S阴=S正方形O1O2O3O4-S空白”,考虑到四个圆半径相同,若延长O2O1交⊙O1于A,则S空白=4SO1AB,由(1)根据对称性可求SO1BO4,再由“SO1AB=S扇形AO1O4-SO1BO4”,这样S空白可求.
解答 (1)设两圆交于A、B两点,连结O1A,O2A,O1B,O2B.
则S阴=S菱形AO1BO2+4S弓.
∵S菱形=2S△AO1O2,△O1O2A为正△,其边长为r.
∴S△AO1O2=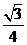 r2,S弓=
r2,S弓=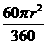 -
-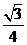 r2=
r2=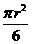 -
-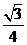 r2.
r2.
∴S阴=2×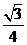 r2+4(
r2+4(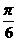 r2-
r2-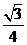 r2)=
r2)=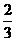
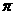 r2-
r2-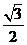 r2.
r2.
(2)图2阴影部分的面积为S阴=S△O1O2O3+3S弓.
∵△O1O2O3为正△,边长为r.
∴S△O1O2O3=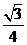 r2,S弓=
r2,S弓=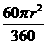 -
-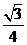 r2.
r2.
∴S阴=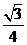 r2+3(
r2+3(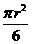 -
-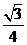 r2)=
r2)=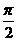 r2-
r2-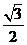 r2.
r2.
(3)延长O2O1与⊙O1交于点A,设⊙O1与⊙O4交于点B,由(1)知,SO1BO4=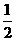 (
(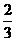
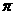 r2-
r2-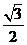 r2).
r2).
∵SO1AB=S扇形AO1O4-SO1BO4
=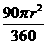 -
-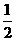 (
(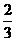
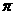 r2=
r2=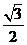 r2)
r2)
=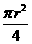 -
-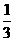
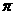 r2+
r2+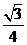 r2.
r2.
则S阴=S正方形O1O2O3O4-4SO1AB
=r2-4(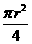 -
-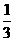
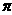 r2+
r2+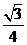 r2)
r2)
=r2+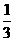
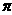 r2-
r2-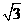 r2=(
r2=(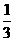
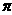 +1-
+1-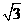 )r2.
)r2.
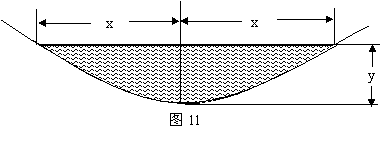
2、如图11是某段河床横断面的示意图.查阅该河段的水文资料,得到下表中的数据:

|
x(米) |
5 |
10 |
20 |
30 |
40 |
50 |
|
y(米) |
0.125 |
0.5 |
2 |
4.5 |
8 |
12.5 |
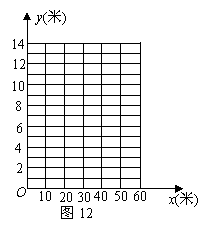 (1)请你以上表中的各对数据(x,y)作为点的坐标,尝试在图12所示的坐标系中画出y关于x的函数图象;
(1)请你以上表中的各对数据(x,y)作为点的坐标,尝试在图12所示的坐标系中画出y关于x的函数图象;
(2)①填写下表:
|
x |
5 |
10 |
20 |
30 |
40 |
50 |
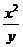 |
|
|
|
|
|
|
②根据所填表中数据呈现的规律,猜想出用x表示y 的二次函数的表达式:_______.
(3)当水面宽度为36米时,一艘吃水深度(船底部到水面的距离)为1.8米的货船能否在这个河段安全通过?为什么?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com