3．下列调查适合普查的是　　　　　　　　　　　　　　　　　 [　　 ]

A．调查2009年6月份市场上某品牌饮料的质量

B．了解中央电视台直播北京奥运会开幕式的全国收视率情况

C． 环保部门调查5月份黄河某段水域的水质量情况

D．了解全班同学本周末参加社区活动的时间

[解析]适合普查的方式一般有以下几种：①范围较小；②容易掌控；③不具有破坏性；④可操作性较强。基于以上各点，“了解全班同学本周末参加社区活动的时间”适合普查，其它几项都不符合以上特点，不适合普查。

答案：D

2．不等式－2x＜4的解集是　　　　　　　　　　　　　　　　　 [　　 ]

A．x＞－2　　　　　　　 B．x＜－2　　　　　　　　 C． x＞2　　　　　　　　 D． x＜2

[解析]两边同除以－2，得x＞－2.本题考查了不等式的性质3：不等式两边同除以同一个负数，不等号的方向改变。在这一点上学生容易想不到改变不等号的方向误选B，而导致错误的发生。

答案：A

1．－5的相反数是　　　　　　　　　　　　　　　　　　　　 [　　 ]

A．　　　　　　　　　　　 B．－　　　　　　　　　　 C． －5　　　　　　　　　 D． 5

[解析]－(－5)＝5.本题考查了相反数的意义，一个数的相反数就是在这个数前面添上“－”号：一个正数的相反数是负数，一个负数的相反数是正数，0的相反数是0。学生易把相反数的意义与倒数的意义混淆，误认为－5的相反数是－而导致错误。

答案：D

25．(12分)如图，有长为30m的篱笆，一面利用墙(墙的最大可用长度为10m)，围成中间隔有一道篱笆(平行于AB)的矩形花圃．设花圃的一边AB为xm，面积为ym²．

(1)求y与x的函数关系式；(3分)

(2)如果要围成面积为63m²的花圃，AB的长是多少？(4分)

答案：解：(1)y＝x(30－3x)　 即y＝－3x²+30x　　　 3分

(2)当y＝63时，－3x²+30x＝63.

解此方程得x₁＝7，x₂＝3.　 5分

当x＝7时, 30－3x＝9＜10，符合题意；

当x＝3时, 30－3x＝21＞10，不符合题意，舍去；

∴当AB的长为7m时，花圃的面积为63cm².　　　　　 7分

(3)能.　　　　 8分

y＝－3x²+30x＝－3(x－5)²+75 9分

而由题意：0＜30－3x≤10，得≤x＜10　　11分

又当x＞5时，y随x的增大而减小，

∴当x＝m时面积最大，最大面积为66m².　　 12分

24．(12分)光明灯具厂生产一批台灯罩，如图的阴影部分为灯罩的侧面展开图．已知半径OA、OC分别为36cm、12cm，∠AOB＝135º．

(1)若要在灯罩的上下边缘镶上花边(花边的宽度忽略不计)，需要多长的花边？(6分)

(2)求灯罩的侧面积(接缝不计)．(6分)

(以上计算结果保留)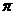

答案：解：(1)⌒AB的长＝＝27π 2分

⌒CD的长＝＝9π　　　 4分

∴花边的总长度＝(2π×36－27π)+(2π×12－9π)＝60π(cm)　 6分

(2)S_扇形OAB＝＝486π.　　　 8分

S_扇形OCD＝＝54π　 10分

S_侧＝S阴影＝(π×36²－S_扇形OAB)－(π×12²－S_扇形OCD)=720π(cm²)　　 12分

22．(10分)小颖准备到甲、乙两个商场去应聘．如图，l₁、l₂分别表示了甲、乙两商场每月付给员工工资y₁、y₂(元)与销售商品的件数x(件)的关系．

(1)根据图象分别求出y₁、y₂与x的函数关系式；(7分)

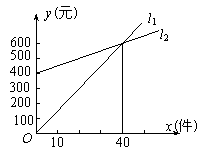(2)根据图象直接回答：如果小颖决定应聘，她可能选择甲商场还是乙商场？(3分)

答案：解：(1)y₁与x的函数关系式为：y₁＝15x.　　 　　3分

y₂与x的函数关系式为：y₂＝5x+400.　　　　　7分

(2)当销售件数大于40件时，选择甲商场；　　　　8分

　当销售件数小于40件时，选择乙商场；　　　　9分

　当销售件数等于40件时，选择甲商场或乙商场都一样.　10分

23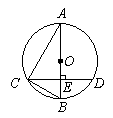．(10分)如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，连接AC、BC，若∠BAC＝60º，CD＝6cm．

(1)求∠BCD的度数；(4分)

(2)求⊙O的直径．(6分)

答案：解：(1)∵直径AB⊥CD，

∴⌒BC＝⌒BD　　 2分

∴∠DCB＝∠CAB＝30°　　 4分

(2)∵直径AB⊥CD,CD＝6，

∴CE＝3 6分

在Rt△ACE中，∠A＝30°，

∴AC＝6 8分

∵AB是直径，∴∠ACB＝90°

在Rt△ACB中，AB＝＝＝4(cm)　 10分

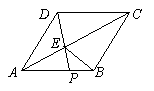
21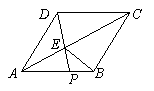．(12分)如图，在菱形ABCD中，P是AB上的一个动点(不与A、B重合)．连接OP交对角线AC于E连接BE．

(1)证明：∠APD＝∠CBE；(6分)

(2)若∠DAB＝60º，试问P点运动到什么位置时，△ADP

的面积等于菱形ABCD面积的？为什么？(6分)

答案：(1)证明：∵四边形ABCD是菱形，

∴BC＝CD，AC平分∠BCD.　　　 2分

而CE＝CE，

∴△BCE≌△DCE.　　　 4分

∴∠EBC＝∠EDC.

又AB∥DC，

∴∠APD＝∠CDP.　　　 5分

∴∠EBC＝∠APD.　　　 6分

(2)当P点运动到AB边的中点时，S_△ADP＝S_菱形ABCD .　　 8分

连结DB，

∵∠DAB＝60°，AD＝AB，

∴△ABD等边三角形.　 9分

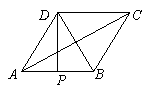而P是AB边的中点，

∴DP⊥AB　　 10分

∴S_△ADP＝AP·DP ,S_菱形ABCD＝AB·DP　 　　 　　11分

∵AP＝AB

∴S_△ADP＝×AB·DP＝S_菱形ABCD.

即△ADP的面积等于菱形ABCD面积的　　　12分

20．(10分)现有分别标有数字1、2、3、4、5、6的6个质地和大小完全相同的小球．

(1)若6个小球都装在一个不透明的口袋中，从中随机摸出一个，其标号为偶数的概率为多少？(4分)

(2)若将标有数字1、2、3的小球装在不透明的甲袋中，标有数字4、5、6的小球装在不透明的乙袋中，现从甲、乙两个口袋中各随机摸出一个球，用列表(或树状图)法，表示所有可能出现的结果，并求摸出的两个球上数字之和为6的概率．(6分)

答案：解：(1)∵6个数中有3个偶数，

∴选中标号为偶数的概率是　　 4分

(2) 所有可能出现的结果列表为：

	4	5	6
1	(1，4)	(1，5)	(1，6)
2	(2，4)	(2，5)	(2，6)
3	(3，4)	(3，5)	开始 　 (3，6)

或列树状图为

列表或画树状图。　　　 8分

P(两个球上数字之和为6)＝ 10分

19．(9分)某马戏团有一架如图所示的滑梯，滑梯底端B到立柱AC的距离BC为8m，在点B处测得点D和滑梯顶端A处的仰角分别为26.57º和36.87º．

(1)求点A到点D的距离(结果保留整数)；(5分)

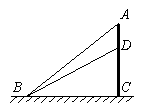(2)在一次表演时，有两只猴子在点D处听到驯兽员的召唤，甲猴由D顺着立柱下到底端C，再跑到B；乙猴由D爬到滑梯顶端A，再沿滑道AB滑至B．小明看完表演后，他认为甲、乙两只猴子所经过的路程大致相等，小明的判断正确吗？通过计算说明．(4分)

答案：(1)在Rt△ABC中，BC=8，∠ABC＝36.87°

∴AC＝8·tan36.87°≈6(米) 2分

在Rt△DBC中，BC=8，∠DBC＝26.57°

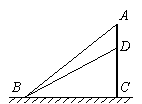∴DC＝8·tan26.57°≈4(米) 4分

∴AD＝AC－DC＝2(米)

即从A点到D点的距离约是2米.　　5分

(2)∵AB＝＝10(米)　　7分

[或在Rt△ABC中，BC=8，∠ABC＝36.87°

∴AB＝≈10(米)　　　　　 7分 ]

∴甲所走的路程为：10+2＝12(米)

乙所走的路程为：8+4＝12(米)　8分

∴小明的判断是正确的.　　　　9分

18．(10分)为了解某中学九年级学生中考体育成绩情况，现从中抽取部分学生的体育成绩进行分段(A：50分、B：49-40分、C：39-30分、D：29-0分)统计结果如图1、图2所示．

根据上面提供的信息，回答下列问题：

(1)本次抽查了多少名学生的体育成绩？(2分)

(2)在图1中，将选项B的部分补充完整？(3分)

(3)求图2中D部分所占的比例；(2分)

(4)已知该校九年级共有900名学生，请估计该校九年级学生体育成绩达到40分以上(含40分)的人数．(3分)

答案：解(1)根据统计图可知，A的人数为80人，A占被调查人数的16%，所以本次调查的人数为80÷16%＝500(人)··················· 　　　　(2分)

(2)由分数段百分比统计图知B的人数占被调查人数的40%，所以B的人数为500×40%＝200(人)

在分数段统计图中将B的部分补充如图所示.　　(5分)

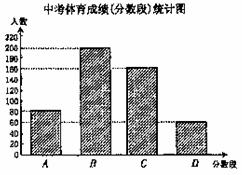
(3)在分数段百分比统计图中阴影部分学生所占的比例：60÷500＝12%.　　(7分)

(4)该校九年级学生体育成绩达到40分以上(含40分)的人数为90×56%＝504(人)(10分)