13．在一个不透明的袋子中有2个黑球、3个白球，它们除颜色外其他均相同.充分摇匀后,先摸出1个球不放回,再摸出1个球,那么两个球都是黑球的概率为 　　　　　　　　　.

[解析]通过列表或画树状图，很容易得出答案。本题考查了统计与概率的相关知识，学生由于审题不清，忽略了“不放回”而得出错误结果。本题也可利用“总概率等于分概率之积”来解决，即第一次摸到黑球的概率为，不放回，第二次摸到黑球的概率为，于是两次都摸到黑球的概率为＝。

答案：

12．点A(2，1)在反比例函数y＝的图像上，当1＜x＜4时，y的取值范围是　　　　　　　 .

[解析]先确定k值：k＝2，再把x所取范围的两个端点值代入，求得y值分别为和2，再根据“在每个象限内，y随x的增大而减小”，可得＜y＜2。本题考查了反比例函数表达式的确定及反比例函数的性质，对于极端值的灵活运用，是学生解决此类问题的难点。

答案：＜y＜2

11．如图，AB为半圆O的直径，延长AB到点P，使BP＝AB，PC切半圆O于点C，点D是⌒AC上和点C不重合的一点，则∠D的度数为　　　　　　　 .

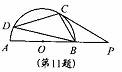
[解析]连接OC，由切线的性质得OC⊥PC，于是易得Rt△OCP中，OC＝OB＝PB，利用30°所对的边等于斜边的一半，可得∠P＝30°，于是得∠COP＝60°再由“同弧所对的圆周角等于它所对的圆心角的一半”得∠D＝30°.本题考查了直角三角形中30°角的确定及圆周角与圆心角的关系，属综合性稍强的题目，学生由于应用中的某一类知识欠缺导致出现错误。

答案：30°

10．如图,在□ABCD中，AC与BD交于点O，点E是BC边的中点，OE＝1,则AB的长是　　　　 .

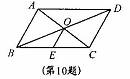
[解析]由平行四边形可知O为AC的中点，而E为BC的中点，可得OE为△ABC的中位线，所以OE＝AB，由OE＝1，得AB＝2.本题考查了三角形的中位线的性质：三角形的中位线平行于第三边，且等于第三边的一半。有的学生不会判定三角形的中位线或不理解三角形的中位线的性质，是造成错误的主要原因。

答案：2

9．下图是一个简单的运算程序.若输入X的值为﹣2,则输出的数值为　　　　　　　 .

输入x→x²→+2→输出

[解析]本题其实是代数式求值的问题，即当x＝－2时，求x²+2的值。如果能理解了算式实际表达的意思，直接代入即可求得结果，学生的困难在于理解不了表格式运算程序，从而造成失误。也有学生把(－2)²当成了－4，从而得到错误结果－2.

答案：6

8．如图，AB//CD,CE平分∠ACD，若∠1＝25⁰，那么∠2的度数是　　　　　　　 　.

[解析]本题考查了角平分线的定义及平行线的性质中。先由角平分线的定义求得∠ACD＝50°，再由“两直线平行，同位角相等”得∠2＝50°.

答案：50°

7．16的平方根是　　　　　　 .

[解析]±＝±4.本题考查平方根的意义：一个正数有两个平方根，它们互为相反数，0的平方根是0，负数没有平方根。学生容易把平方根与算术平方根混淆，出现“16的平方根是4”的错误。

答案：±4

6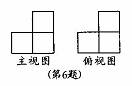．一个几何体由一些大小相同的小正方体组成，如图是它的主视图和俯视图，那么组成该几何体所需小正方体的个数最少为　　　　　　　　　　 [　　 ]

A．3

B． 4

C． 5

D．6

[解析]本题主要考查三视图的相关知识：主视图主要确定物体的长和高，左视图确定物体的宽和高，俯视图确定物体的长和宽。由题中所给出的主视图知物体共两列，且左侧一列高一层，右侧一列最高两层；由俯视图可知左侧一行，右侧两行，于是，可确定左侧只有一个小正方体，而右侧可能是一行单层一行两层，出可能两行都是两层。所以图中的小正方体最少4块，最多5块。

答案：D

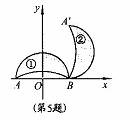
5．如图所示，在平面直角坐标系中，点A、B的坐标分别为(－2，0)和(2，0).月牙①绕点B顺时针旋转90⁰得到月牙②，则点A的对应点A’的坐标为　 　　　　　[　　 ]

A．(2，2)

B．(2，4)

C．(4，2)

D．(1，2)

[解析]旋转不改变图形的形状、大小及相对位置，连接A’B，由月牙①顺时针旋转90°得月牙②，可知A’B⊥AB，且A′B＝AB，由A(－2，0)、B(2，0)得AB＝4，于是可得A’的坐标为(2，4).本题主要考查平面直角坐标系及图形的旋转变换的相关知识，学生往往因理解不透题意而出现问题。

答案：B

4．方程x²＝x的解是　　　　　　　　　　　　　　　　　　　　 [　　 ]

A．x＝1　　　　　　　　　　　　　　　　　　　　　　　　　 B．x＝0

C． x₁＝1，x₂＝0　　　　　　　　　　　　　　　　　 D． x₁＝－1，x₂＝0

[解析]x²－x＝0，x(x－1)＝0，x₁＝1，x₂＝0.本题主要考查一元二次方程的一般解法及等式的基本性质，学生易把方程两边都除以x，得x＝1，这里忽略了x是否为0的验证，导致丢掉方程的一个根，而错误地选择A。

答案：C