
题目列表(包括答案和解析)
6.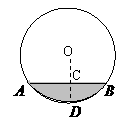 如图,水平放置的一个油管的截面半径为13cm,其中有油部分油面宽
如图,水平放置的一个油管的截面半径为13cm,其中有油部分油面宽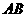 为24cm,则截面上有油部分油面高
为24cm,则截面上有油部分油面高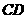 (单位:cm)等于 ( )
(单位:cm)等于 ( )
(A)8cm (B)9cm (C)10cm (D)11cm
5.如图,将正方形图案绕中心O旋转1800 后,得到的图案是( )

4.下列方程中,有两个不等实数根的是( )
A.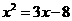 B.
B.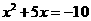
C.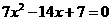 D.
D.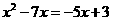
3. 函数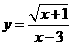 中自变量x的取值范围是 ( )
中自变量x的取值范围是 ( )
A.
x≥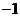 B. x≠3 C.
x≥
B. x≠3 C.
x≥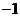 且x≠3 D.
且x≠3 D. 
2. 解方程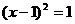 得
( )
得
( )
A.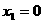 ,
,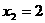 B.
B.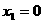 ,
,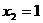 C.
C.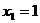 ,
,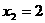 D.
D.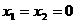
1. 化简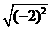 的结果是 ( )
的结果是 ( )
A.一2 B 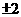 C. 2 D. 4
C. 2 D. 4
28.(本题满分10分)
2009年5月17日至21日,甲型H1N1流感在日本迅速蔓延,每天的新增病例和累计确诊病例人数如图所示.
(1) 在5月17日至5月21日这5天中,日本新增甲型H1N1流感病例最多的是哪一天?该天增加了多少人?
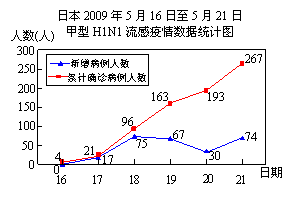 (2) 在5月17日至5月21日这5天中,日本平均每天新增加甲型H1N1流感确诊病例多少人?如果接下来的5天中,继续按这个平均数增加,那么到5月26日,日本甲型H1N1流感累计确诊病例将会达到多少人?
(2) 在5月17日至5月21日这5天中,日本平均每天新增加甲型H1N1流感确诊病例多少人?如果接下来的5天中,继续按这个平均数增加,那么到5月26日,日本甲型H1N1流感累计确诊病例将会达到多少人?
(3) 甲型H1N1流感病毒的传染性极强,某地因1人患了甲型H1N1流感没有及时隔离治疗,经过两天传染后共有9人患了甲型H1N1流感,每天传染中平均一个人传染了几个人?如果按照这个传染速度,再经过5天的传染后,这个地区一共将会有多少人患甲型H1N1流感?
29(本题满分12分)
如图甲,在 中,
中, 为锐角,点
为锐角,点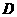 为射线
为射线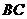 上一点,连接
上一点,连接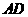 ,以
,以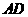 为一边且在
为一边且在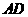 的右侧作正方形
的右侧作正方形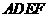 .
.
解答下列问题:
(1)如果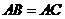 ,
,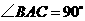 ,
,
①当点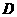 在线段
在线段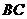 上时(与点
上时(与点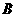 不重合),如图乙,线段
不重合),如图乙,线段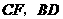 之间的位置关系为 ,数量关系为
.
之间的位置关系为 ,数量关系为
.
②当点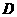 在线段
在线段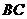 的延长线时,如图丙,①中的结论是否仍然成立,为什么?
的延长线时,如图丙,①中的结论是否仍然成立,为什么?

(2)如果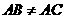 ,
,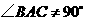 ,点
,点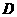 在线段
在线段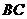 上运动.
上运动.
试探究:当 满足一个什么条件时,
满足一个什么条件时,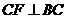 (点
(点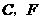 重合除外)?画出相应图形,并说明理由.(画图不写作法)
重合除外)?画出相应图形,并说明理由.(画图不写作法)
27.(本题满分10分) 27题图
如图,在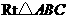 中,
中,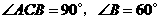 ,
,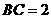 .点
.点 是
是 的中点,过点
的中点,过点 的直线
的直线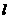 从与
从与 重合的位置开始,绕点
重合的位置开始,绕点 作逆时针旋转,交
作逆时针旋转,交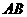 边于点
边于点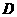 .过点
.过点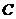 作
作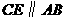 交直线
交直线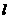 于点
于点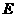 ,设直线
,设直线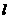 的旋转角为
的旋转角为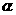 .
.
(1)①当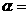 度时,四边形
度时,四边形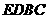 是等腰梯形,此时
是等腰梯形,此时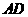 的长为 ;
的长为 ;
②当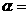 度时,四边形
度时,四边形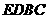 是直角梯形,此时
是直角梯形,此时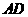 的长为 ;
的长为 ;
(2)当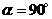 时,判断四边形
时,判断四边形 是否为菱形,并说明理由
是否为菱形,并说明理由
26.(10分)
直角三角形通过剪切可以拼成一个与该直角三角形面积相等的矩形,方法如下:
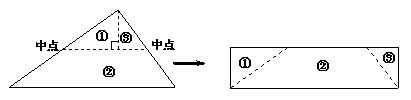
请你用上面图示方法,解答下列问题:
(1)对任意三角形,设计一种方案,将它分成若干块,再拼成一个与原三角形面积相等的矩形.
(2)对任意四边形,设计一种方案,将它分成若干块,
再拼成一个与原四边形面积相等的矩形.
25.(本小题满分9分)
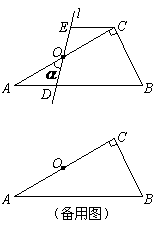
(1)观察与发现: 小明将三角形纸片ABC(AB >AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图①);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图②).小明认为△AEF是等腰三角形,你同意吗?请说明理由.
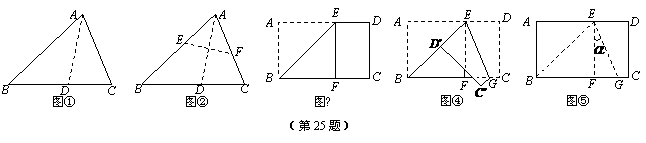 (2)实践与运用:将矩形纸片ABCD沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图③);再沿过点E的直线折叠,使点D落在BE上的点D′处,折痕为EG(如图④);再展平纸片(如图⑤).求图⑤中∠α的大小.
(2)实践与运用:将矩形纸片ABCD沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图③);再沿过点E的直线折叠,使点D落在BE上的点D′处,折痕为EG(如图④);再展平纸片(如图⑤).求图⑤中∠α的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com