3.　　 在x轴上是否存在点P，使△AOP为等腰三角形？若存在，把符合条件的P点坐标直接写出来，若不存在请说明理由。

2.　　 求△AOB的面积。

1.　　 求反比例函数和一次函数的表达式。

23.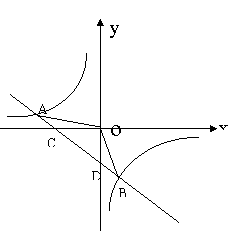 (本题满分12分)如图，一次函数y=ax+b的图像与反比例函数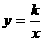的图像交于A、B两点，与x轴交于点C，与y轴交于点D，已知OA=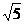，tan∠AOC=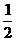，点B 的坐标为(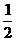，m)

22．(本题满分10分)

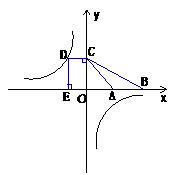D为反比例函数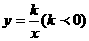：图象上一点.过D作DC⊥y轴于C, DE⊥x轴于E,一次函数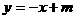与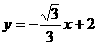的图象都过C点,与x轴分别交于A、B两点。若梯形DCAE的面积为4，求k的值.

21．(本题满分10分)

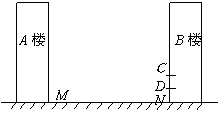
如图，某居民小区内两楼之间的距离米，两楼的高都是20米，楼在楼正南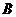，楼窗户朝南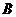．楼内一楼住户的窗台离小区地面的距离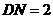米，窗户高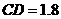米．当正午时刻太阳光线与地面成角时，楼的影子是否影响楼的一楼住户采光？若影响，挡住该住户窗户多高？若不影响，请说明理由．

(参考数据：，，)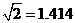

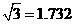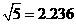20． (本小题满分8分)

如图，在△ABC中，AD是BC上的高，，

　(1) 求证：AC=BD；

(2)若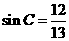，BC=12，求AD的长．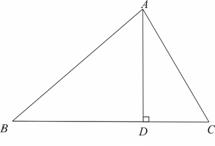

证明过程或演算步骤。

19．(本小题满分8分)

有两个可以自由转动的均匀转盘A、B，分别被分成4等份、3等份，并在每份内均标有数字，如图所示，丁洋和王倩同学用这两个转盘做游戏，游戏规则如下：

(1)分别转动转盘A和B；(2)两个转盘停止后，将两个指针所指份内的数字相加(如果指针恰好停在等分线上，那么重转一次，直到指针指向某一份为止；)(3)如果和为0，丁洋获胜，否则王倩获胜。

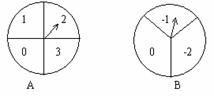(1)用列表法(或树状图)求丁洋获胜的概率；

(2)你认为这个游戏对双方公平吗？请说明理由。

18.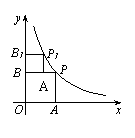如图，已知反比例函数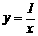的图像上有一点P，过点P分别作x轴和y轴的垂线，垂足分别为A、B，使四边形OAPB为正方形。又在反比例函数的图像上有一点P₁，过点P₁分别作BP和y轴的垂线，垂足分别为A₁、B₁，使四边形BA₁P₁B₁为正方形，则点P₁的坐标是　　　　　　　 。

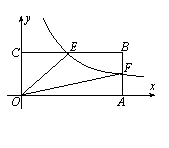
17.如图，已知双曲线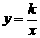(x＞0)经过矩形OABC边AB的中点F，交BC于点E，且四边形OEBF的面积为2，则k＝______________。