
题目列表(包括答案和解析)
1.集合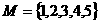 的子集个数是 ( )
的子集个数是 ( )
A.32 B.31 C.16 D.15
23.3二次函数y=ax2+bx+c的图象和性质同步练习
第31题. (济宁课改)二次函数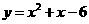 的图象与
的图象与 轴交点的横坐标是( )
轴交点的横坐标是( )
A.2和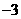 B.
B.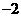 和
和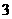 C.2和3 D.
C.2和3 D.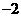 和
和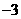
答案:A
第32题. (荆州课改)已知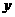 关于
关于 的函数:
的函数: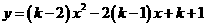 中满足
中满足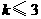 .
.
(1)求证:此函数图象与 轴总有交点.
轴总有交点.
(2)当关于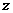 的方程
的方程 有增根时,求上述函数图象与
有增根时,求上述函数图象与 轴的交点坐标.
轴的交点坐标.
答案:(1)当 时,函数为
时,函数为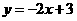 ,图象与
,图象与 轴有交点.
轴有交点.
当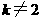 时,
时,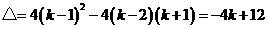
当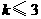 时,
时,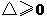 ,此时抛物线与
,此时抛物线与 轴有交点.
轴有交点.
因此,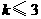 时,
时,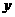 关于
关于 的函数
的函数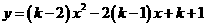 的图象与
的图象与 轴总有交点.
轴总有交点.
(2)关于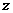 的方程去分母得:
的方程去分母得: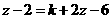 ,
,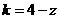 .
.
由于原分式方程有增根,其根必为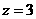 .这时
.这时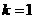 (6分)
(6分)
这时函数为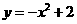 .它与
.它与 轴的交点是
轴的交点是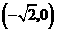 和
和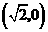
第33题. (苏州课改)抛物线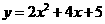 的对称轴是
的对称轴是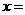 ______.
______.
答案: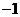
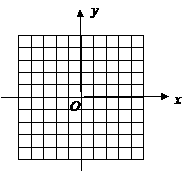 第34题. (安徽课改)抛物线
第34题. (安徽课改)抛物线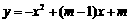 与
与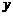 轴交于
轴交于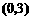 点.
点.
(1)求出 的值并画出这条抛物线;
的值并画出这条抛物线;
(2)求它与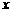 轴的交点和抛物线顶点的坐标;
轴的交点和抛物线顶点的坐标;
(3)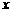 取什么值时,抛物线在
取什么值时,抛物线在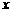 轴上方?
轴上方?
(4)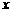 取什么值时,
取什么值时,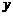 的值随
的值随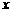 值的增大而减小?
值的增大而减小?
[解]
答案:解:(1)由抛物线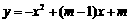 与
与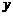 轴交于
轴交于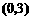 ,得:
,得: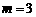 .
.
 抛物线为
抛物线为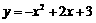 .图象略.
.图象略.
(2)由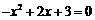 ,得
,得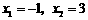 .
.
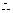 抛物线与
抛物线与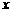 轴的交点为
轴的交点为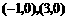 .
.
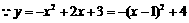 ,
,
 抛物线顶点坐标为
抛物线顶点坐标为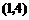 .
.
(3)由图象可知:
当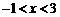 时,抛物线在
时,抛物线在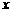 轴上方.
轴上方.
(4)由图象可知:
当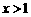 时,
时,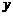 的值随
的值随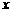 值的增大而减小.
值的增大而减小.
第35题. (贺州课改)已知抛物线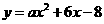 与直线
与直线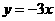 相交于点
相交于点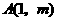 .
.
(1)求抛物线的解析式;
(2)请问(1)中的抛物线经过怎样的平移就可以得到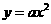 的图象?
的图象?
(3)设抛物线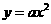 上依次有点
上依次有点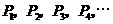 ,其中横坐标依次是
,其中横坐标依次是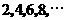 ,纵坐标依次为
,纵坐标依次为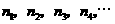 ,试求
,试求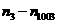 的值.
的值.
答案:解:(1) 点
点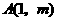 在直线
在直线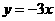 上,
上,
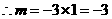 .
.
把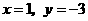 代入
代入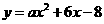 ,
,
得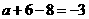 .求得
.求得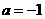 .
.
 抛物线的解析式是
抛物线的解析式是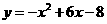 .
.
(2)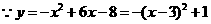 .
.
 顶点坐标为
顶点坐标为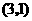 .
.
 把抛物线
把抛物线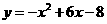 向左平移3个单位长度得到
向左平移3个单位长度得到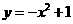 的图象,再把
的图象,再把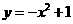 的图象向下平移1个单位长度得到
的图象向下平移1个单位长度得到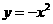 的图象.
的图象.
(3)由题意知,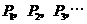 的横坐标是连续偶数,所以
的横坐标是连续偶数,所以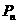 的横坐标是
的横坐标是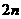 ,纵坐标为
,纵坐标为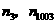 所对应的纵坐标依次是
所对应的纵坐标依次是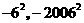 .
.
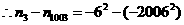
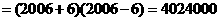 .
.
第36题. (湖南永州非课改)观察下列四个函数的图象( )

将它们的序号与下列函数的排列顺序:正比例函数、一次函数、二次函数、反比例函数,对应正确的是( )
A.①②③④ B.②③①④ C.③②④① D.④②①③
答案:C
第37题. (沈阳非课改)抛物线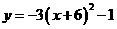 的对称轴是直线( )
的对称轴是直线( )
A.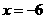 B.
B.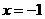 C.
C.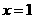 D.
D.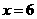
答案:A
第38题. (兰州A课改)请选择一组你喜欢的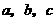 的值,使二次函数
的值,使二次函数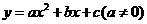 的图象同时满足下列条件:①开口向下,②当
的图象同时满足下列条件:①开口向下,②当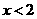 时,
时,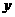 随
随 的增大而增大;当
的增大而增大;当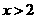 时,
时,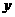 随
随 的增大而减小.这样的二次函数的解析式可以是 .
的增大而减小.这样的二次函数的解析式可以是 .
答案:答案不唯一,只要满足对称轴是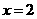 ,
,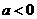 .
.
第39题. (兰州A课改)已知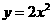 的图象是抛物线,若抛物线不动,把
的图象是抛物线,若抛物线不动,把 轴,
轴,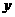 轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是( ).
轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是( ).
A.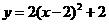 B.
B.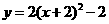
C.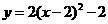 D.
D.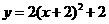
答案:B
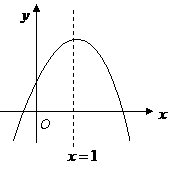
第40题. (兰州A课改)已知二次函数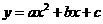 的图象如图所示,对称轴是
的图象如图所示,对称轴是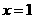 ,则下列结论中正确的是( ).
,则下列结论中正确的是( ).
A.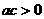 B.
B.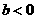
C. D.
D.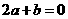
答案:D
第41题. (辽宁十一市课改)已知二次函数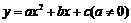 ,其中
,其中 满足
满足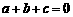 和
和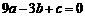 ,则该二次函数图象的对称轴是直线 .
,则该二次函数图象的对称轴是直线 .
答案: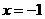
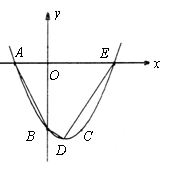
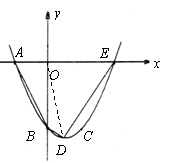
第42题. (辽宁十一市非课改)如图,已知抛物线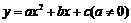 经过
经过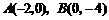 ,
,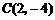 三点,且与
三点,且与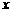 轴的另一个交点为
轴的另一个交点为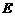 .
.
(1)求抛物线的解析式;
(2)用配方法求抛物线的顶点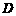 的坐标和对称轴;
的坐标和对称轴;
(3)求四边形 的面积.
的面积.
答案:解:(1) 抛物线
抛物线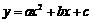 经过
经过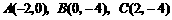 三点
三点
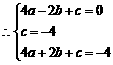 解得
解得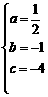
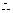 抛物线解析式:
抛物线解析式: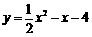 .
.
(2)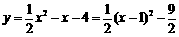
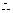 顶点坐标
顶点坐标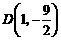 ,对称轴:
,对称轴: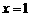 .
.
(3)连结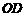 ,对于抛物线解析式
,对于抛物线解析式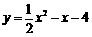
当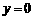 时,得
时,得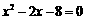 ,解得:
,解得: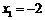 ,
,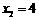
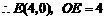
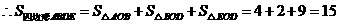 .
.
第43题. (浙江湖州课改)已知二次函数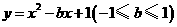 ,当
,当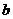 从
从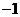 逐渐变化到
逐渐变化到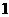 的过程中,它所对应的抛物线位置也随之变动.下列关于抛物线的移动方向的描述中,正确的是( )
的过程中,它所对应的抛物线位置也随之变动.下列关于抛物线的移动方向的描述中,正确的是( )
A.先往左上方移动,再往左下方移动 B.先往左下方移动,再往左上方移动
C.先往右上方移动,再往右下方移动 D.先往右下方移动,再往右上方移动
答案:C
第44题. (江西课改)二次函数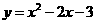 的最小值是 .
的最小值是 .
答案: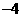
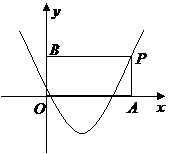
第45题. (长春课改)如图,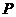 为抛物线
为抛物线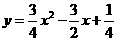 上对称轴右侧的一点,且点
上对称轴右侧的一点,且点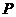 在
在 轴上方,过点
轴上方,过点 作
作 垂直
垂直 轴于点
轴于点 ,
,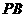 垂直
垂直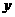 轴于点
轴于点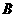 ,得到矩形
,得到矩形 .若
.若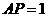 ,求矩形
,求矩形 的面积.
的面积.
答案: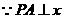 轴,
轴,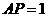 ,
, 点
点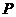 的纵坐标为
的纵坐标为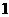 .
.
当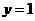 时,
时,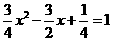 ,即
,即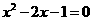 .
.
解得 .
.
 抛物线的对称轴为
抛物线的对称轴为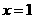 ,点
,点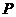 在对称轴的右侧,
在对称轴的右侧,
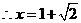 .
.
 矩形
矩形 的面积为
的面积为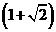 个平方单位.
个平方单位.
第46题. 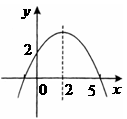 (山西非课改)二次函数
(山西非课改)二次函数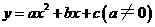 的图象如图所示.
的图象如图所示.
有下列结论:① ;②
;②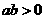 ;③
;③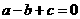 ;④
;④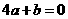 ;⑤当
;⑤当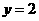 时,
时, 只能等于
只能等于 .其中正确的是( )
.其中正确的是( )
A.①④ B.③④ C.②⑤ D.③⑤
答案:B
第47题. (威海非课改)抛物线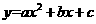
 过点
过点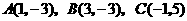 ,顶点为
,顶点为 M点.
M点.
(1)求该抛物线的解析式.
(2)试判断抛物线上是否存在一点P,使∠POM=90˚.
若不存在,说明理由;若存在,求出P点的坐标.
(3)试判断抛物线上是否存在一点K,使∠OMK=90˚,
说明理由.
答案:解:(1)根据题意,得

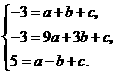
解,得 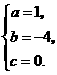
∴
抛物线的解析式为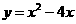 .
.
(2)抛物线上存在一点P,使∠POM=90˚.
x=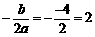 ,
,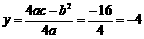 .
.
∴ 顶点M的坐标为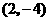 .
.
设抛物线上存在一点P,满足OP⊥OM,其坐标为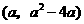 .
.
过P点作PE⊥y轴,垂足为E;过M点作MF⊥y轴,垂足为F.
则 ∠POE+∠MOF=90˚,∠POE+∠EPO=90˚.
∴ ∠EPO=∠FOM.
∵ ∠OEP=∠MFO=90˚,
∴ Rt△OEP∽Rt△MFO.
∴ OE∶MF=EP∶OF.
即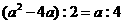 .
.
解,得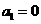 (舍去),
(舍去),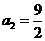 .
.
∴ P点的坐标为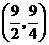 .
.
(3)过顶点M作MN⊥OM,交y轴于点N.则 ∠FMN+∠OMF=90˚.
∵ ∠MOF+∠OMF=90˚,
∴ ∠MOF=∠FMN.
又∵ ∠OFM=∠MFN=90˚,
∴ △OFM∽△MFN.
∴ OF∶MF=MF∶FN. 即 4∶2=2∶FN.∴ FN=1.
∴ 点N的坐标为(0,-5).
设过点M,N的直线的解析式为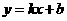 .
.
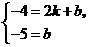 解,得
解,得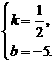 直线的解析式为
直线的解析式为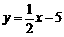 .
.
∴ 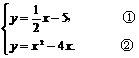 把①代入②,得
把①代入②,得 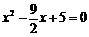 .
.
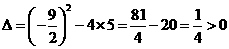 .
.
∴ 直线MN与抛物线有两个交点(其中一点为顶点M).
∴ 抛物线上必存在一点K,使∠OMK=90˚.
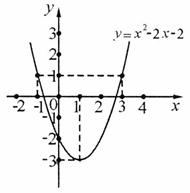
第48题. (资阳课改)已知函数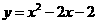 的图象如图3所示,根据其中提供的信息,可求得使
的图象如图3所示,根据其中提供的信息,可求得使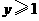 成立的
成立的 的取值范围是( )
的取值范围是( )
A.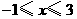 B.
B.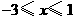
C.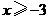 D.
D.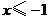 或
或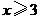
答案:D
第49题. (安徽非课改)请你写出一个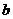 的值,使得函数
的值,使得函数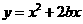 在第一象限内
在第一象限内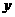 的值随着
的值随着 的值增大而增大,则
的值增大而增大,则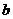 可以是 .
可以是 .
答案:答案不唯一,如0;1;2等
第50题. (南充课改)二次函数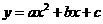 中,
中,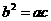 ,且
,且 时
时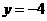 ,则( )
,则( )
A.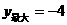 B.
B.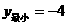 C.
C.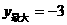 D.
D.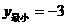
答案:C
第51题. (徐州非课改)下表给出了代数式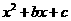 与
与 的一些对应值:
的一些对应值:
 |
… |
0 |
1 |
2 |
3 |
4 |
… |
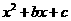 |
… |
3 |
|
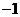 |
|
3 |
… |
(1)请在表内的空格中填入适当的数;
(2)设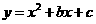 ,则当
,则当 取何值时,
取何值时,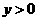 ?
?
(3)请说明经过怎样平移函数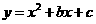 的图象得到函数
的图象得到函数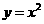 的图象.
的图象.
答案:(1)0,0;
(2)当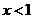 或
或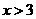 时,
时,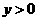 .(写出
.(写出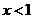 或
或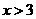 中的一个得1分)
中的一个得1分)
(用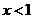 和
和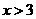 中的特殊值说明得1分,只用
中的特殊值说明得1分,只用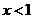 或
或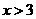 中的特殊值说明不得分)
中的特殊值说明不得分)
(3)由(1)得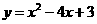 ,即
,即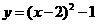 ,
,
将抛物线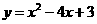 先向左平移2个单位(1分),再向上平移1个单位(1分)即得抛物线
先向左平移2个单位(1分),再向上平移1个单位(1分)即得抛物线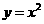 .
.
(配方正确,并说明将抛物线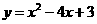 的顶点移到原点得2分;不配方,但说明将抛物线
的顶点移到原点得2分;不配方,但说明将抛物线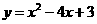 的顶点
的顶点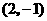 移到原点得2分;不配方,只说明将抛物线的顶点移到原点不得分)
移到原点得2分;不配方,只说明将抛物线的顶点移到原点不得分)
第52题. (龙岩三县非课改)已知抛物线 与
与 轴交于
轴交于 两点,则线段
两点,则线段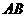 的长度为( )
的长度为( )
A.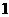 B.
B.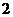 C.
C.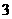 D.
D.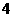
答案:D
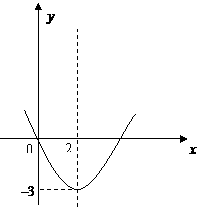
第53题. (岳阳课改)小明从右边的二次函数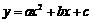 图象中,观察得出了下面的五条信息:
图象中,观察得出了下面的五条信息:
①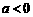 ,②
,②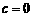 ,③函数的最小值为
,③函数的最小值为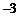 ,④当
,④当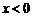 时,
时,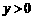 ,⑤当
,⑤当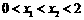 时,
时,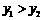 .你认为其中正确的个数为( )
.你认为其中正确的个数为( )
A.2 B.3
C.4 D.5
答案:C
23. 2 二次函数y=a
2 二次函数y=a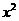 的图象和性质同步练习
的图象和性质同步练习

 第1题. 对于抛物线
第1题. 对于抛物线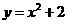 和
和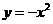 的论断:(1)开口方向不同;(2)形状完全相同;(3)对称轴相同.其中正确的有( )
的论断:(1)开口方向不同;(2)形状完全相同;(3)对称轴相同.其中正确的有( )
 A.0个 B.1个 C. 2个 D.3个
A.0个 B.1个 C. 2个 D.3个
 答案:D
答案:D



 第2题. 下列关于抛物线
第2题. 下列关于抛物线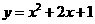 的说法中,正确的是( )
的说法中,正确的是( )
 A.开口向下 B.对称轴是直线x=1
A.开口向下 B.对称轴是直线x=1
 C.与x轴有两个交点 D.顶点坐标是(-1,0)
C.与x轴有两个交点 D.顶点坐标是(-1,0)
 答案:D
答案:D

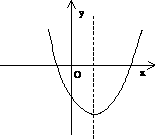

 第3题. 二次函数y=ax2+bx+c(a≠0)的图象如图,a,b,c的取值范围( )
第3题. 二次函数y=ax2+bx+c(a≠0)的图象如图,a,b,c的取值范围( )
 A.a<0,b<0,c<0 B.a<0,b>0,c<0
A.a<0,b<0,c<0 B.a<0,b>0,c<0
 C.a>0,b>0,c<0 D.a>0,b<0,c<0
C.a>0,b>0,c<0 D.a>0,b<0,c<0
 答案:D
答案:D


 第4题. 与抛物线
第4题. 与抛物线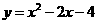 关于y轴对称的图象表示的函数关系式是( )
关于y轴对称的图象表示的函数关系式是( )
 A.
A.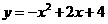 B.
B.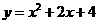
 C.
C.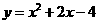 D.
D.
 答案:C
答案:C


 第5题. 若抛物线
第5题. 若抛物线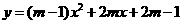 的图象的最低点的纵坐标为零,则m=_______.
的图象的最低点的纵坐标为零,则m=_______.
 答案:
答案: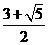


 第6题. 对于抛物线
第6题. 对于抛物线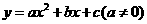 ,当顶点纵坐标等于_________时,顶点在x轴上,此时抛物线与x轴只有一个公共点,而a≠0,所以,抛物线与x轴只有一个公共点的条件是_________.
,当顶点纵坐标等于_________时,顶点在x轴上,此时抛物线与x轴只有一个公共点,而a≠0,所以,抛物线与x轴只有一个公共点的条件是_________.
 答案:0,4ac-b2=0,且a≠0
答案:0,4ac-b2=0,且a≠0


 第7题. 若抛物线
第7题. 若抛物线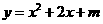 与x轴只有一公共点,则m=_________.
与x轴只有一公共点,则m=_________.
 答案:1
答案:1


 第8题. 函数
第8题. 函数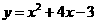 的图象开口向_________,顶点坐标为__________
的图象开口向_________,顶点坐标为__________
 答案:上,(-2,-7)
答案:上,(-2,-7)


 第9题. 二次函数
第9题. 二次函数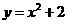 的图象开口_____,对称轴是________,顶点坐标是_______.
的图象开口_____,对称轴是________,顶点坐标是_______.
 答案:向上, y轴,(0,2)
答案:向上, y轴,(0,2)


 第10题. 抛物线
第10题. 抛物线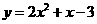 与x轴交点个数为________.
与x轴交点个数为________.
 答案:2个
答案:2个


 第11题. 二次函数
第11题. 二次函数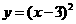 的图象向右平移3个单位,在向上平移1个单位,得到的图象的关系式是____.
的图象向右平移3个单位,在向上平移1个单位,得到的图象的关系式是____.
 答案:
答案: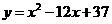 或
或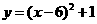


 第12题. 抛物线
第12题. 抛物线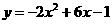 的顶点坐标为_________,对称轴为________.
的顶点坐标为_________,对称轴为________.
 答案:(
答案:(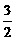 ,
,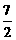 ),x=
),x=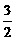


 第13题. 作出下列函数的图象:
第13题. 作出下列函数的图象: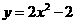
 答案:略
答案:略


 第14题. 作出下列函数的图象:
第14题. 作出下列函数的图象: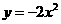
 答案:略
答案:略


 第15题. 用描点法画出下列二次函数的图象:
第15题. 用描点法画出下列二次函数的图象:
 答案:略
答案:略


 第16题. 已知二次函数
第16题. 已知二次函数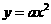 的图象经过点A(-1,1)
的图象经过点A(-1,1)
①
 求这个二次函数的关系式;
求这个二次函数的关系式;
②
 求当x=2时的函数y的值.
求当x=2时的函数y的值.
 答案:
答案: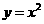 ,
,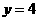


 第17题. 若抛物线
第17题. 若抛物线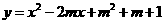 的顶点在第二象限,则常数m的取值范围是( )
的顶点在第二象限,则常数m的取值范围是( )
 A.
A. B.
B.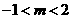
 C.
C.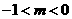 D.
D.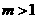
 答案:C
答案:C


 第18题. 如下图,抛物线顶点坐标是P(1,3),则函数y随自变量x的增大而减小的x的取值范围是( )
第18题. 如下图,抛物线顶点坐标是P(1,3),则函数y随自变量x的增大而减小的x的取值范围是( )

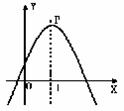 A.x>3 B.x<3 C.x>1 D.x<1
A.x>3 B.x<3 C.x>1 D.x<1
 答案:C
答案:C


 第19题. 二次函数
第19题. 二次函数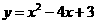 的图象交x轴于A、B两点,交y轴于点C,则△ABC的面积为( )
的图象交x轴于A、B两点,交y轴于点C,则△ABC的面积为( )
 A.6 B.4 C.3 D.1
A.6 B.4 C.3 D.1
 答案:C
答案:C


 第20题. 抛物线
第20题. 抛物线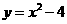 与x轴交于B、C两点,顶点为A,则△ABC的面积为( )
与x轴交于B、C两点,顶点为A,则△ABC的面积为( )
 A 16 B
8 C
4 D
2
A 16 B
8 C
4 D
2
 答案:B
答案:B


 第21题. 若抛物线
第21题. 若抛物线 ,
,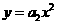 的形状相同,那么( )
的形状相同,那么( )
 A.
A.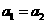 B.
B.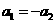
 C.|a1|=|a2| D.a1与a2的关系无法确定
C.|a1|=|a2| D.a1与a2的关系无法确定
 答案:C
答案:C


 第22题. 为了备战世界杯,中国足球队在某次集训中,一队员在距离球门12米处的挑射,正好射中了2.4
第22题. 为了备战世界杯,中国足球队在某次集训中,一队员在距离球门12米处的挑射,正好射中了2.4 米高的球门横梁.若足球运行的路线是抛物线
米高的球门横梁.若足球运行的路线是抛物线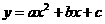 (如图6),则下列结论:①a<
(如图6),则下列结论:①a<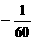 ;②
;②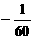 <a<0; ③a-b+c>0;④0<b<-12a.其中正确的是( )
<a<0; ③a-b+c>0;④0<b<-12a.其中正确的是( )
 A.①③ B.①④ C.②③ D.②④
A.①③ B.①④ C.②③ D.②④
 答案:D
答案:D


 第23题. 与抛物线
第23题. 与抛物线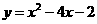 关于x轴对称的图象表示为( )
关于x轴对称的图象表示为( )
 A.
A.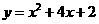 B.
B.
 C.
C.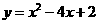 D.
D.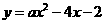
 答案:A
答案:A


 第24题. 若抛物线
第24题. 若抛物线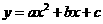 全部在x轴的下方,那么a_________0,同时,b2-4ac_________0.
全部在x轴的下方,那么a_________0,同时,b2-4ac_________0.
 答案:<,<
答案:<,<


 第25题. 把抛物线
第25题. 把抛物线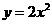 向右平移一个单位,在向下平移3个单位,得到的抛物线的解析式是_________.
向右平移一个单位,在向下平移3个单位,得到的抛物线的解析式是_________.
 答案:
答案: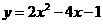


 第26题. 若点(2,-1)在抛物线
第26题. 若点(2,-1)在抛物线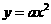 上,那么,当x=2时,y=_________
上,那么,当x=2时,y=_________
 答案:-1
答案:-1


 第27题. 抛物线
第27题. 抛物线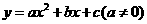 ,关于x轴对称的图象的关系式是_______________.
,关于x轴对称的图象的关系式是_______________.
 答案:
答案: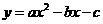


 第28题. 抛物线
第28题. 抛物线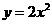 和
和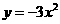 中开口较大的是__________.
中开口较大的是__________.
 答案:
答案: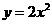


 第29题. 已知抛物线
第29题. 已知抛物线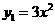 ,另一条抛物线y2的顶点为(2,5),且形状、大小与y1相同,开口方向相反,则抛物线y2的关系式为______________.
,另一条抛物线y2的顶点为(2,5),且形状、大小与y1相同,开口方向相反,则抛物线y2的关系式为______________.
 答案:
答案: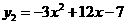


 第30题. 抛物线
第30题. 抛物线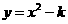 的顶点为P,与x轴交于A、B两点,如果△ABP是正三角形,那么,k=_________.
的顶点为P,与x轴交于A、B两点,如果△ABP是正三角形,那么,k=_________.
 答案:3
答案:3


 第31题. 设二次函数
第31题. 设二次函数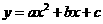 的图象开口向下,顶点在第二象限内.
的图象开口向下,顶点在第二象限内.
 ①确定a,b,
①确定a,b, 的符号;
的符号;
 ②若此二次函数的图象经过原点,且顶点的横坐标与纵坐标互为相反数,顶点与原点的距离为
②若此二次函数的图象经过原点,且顶点的横坐标与纵坐标互为相反数,顶点与原点的距离为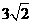 ,求此二次函数的关系式
,求此二次函数的关系式
 答案:① a<0,b<0,b2-4ac>0;
答案:① a<0,b<0,b2-4ac>0;
 ②
②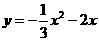


 第32题. 抛物线
第32题. 抛物线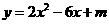 与x轴交于A、B两点,如果要求点A在(0,0)与(1,0)之间,点B在(2,0)与(3,0)之间,请确定m的取值范围
与x轴交于A、B两点,如果要求点A在(0,0)与(1,0)之间,点B在(2,0)与(3,0)之间,请确定m的取值范围
 答案:
答案: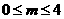


 第33题. 是否存在以y轴为对称轴的抛物线,经过(3,-4)和(-3,4)两点,若存在,请写出抛物线的解析式;若不存在请说明理由.
第33题. 是否存在以y轴为对称轴的抛物线,经过(3,-4)和(-3,4)两点,若存在,请写出抛物线的解析式;若不存在请说明理由.
 答案:不存在.
答案:不存在.
 若存在以y轴为对称轴的抛物线,经过(3,-4)和(-3,4)两点,必然也过他们的对称点(-3,-4)、(3,4)这样,抛物线的解析式便可以有两种形式,y=a(x+3)(x-3)+4和y=a(x+3)(x-3)-4,这样的a不存在
若存在以y轴为对称轴的抛物线,经过(3,-4)和(-3,4)两点,必然也过他们的对称点(-3,-4)、(3,4)这样,抛物线的解析式便可以有两种形式,y=a(x+3)(x-3)+4和y=a(x+3)(x-3)-4,这样的a不存在


 第34题. 若点P(1,a)和Q(-1,b)都在抛物线
第34题. 若点P(1,a)和Q(-1,b)都在抛物线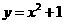 上,则线段PQ的长为_____
上,则线段PQ的长为_____
 答案:2
答案:2


 第35题. 二次函数
第35题. 二次函数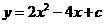 的值永远为正,则c的取值范围是( )
的值永远为正,则c的取值范围是( )
 A.
A.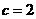 B.
B.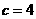 C.
C.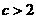 D.
D.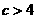
 答案:C
答案:C


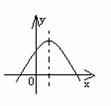
 第36题. 二次函数
第36题. 二次函数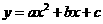 的图象如图,则点M(
的图象如图,则点M(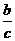 ,a)在( )
,a)在( )
 A.第一象限 B.第二象限
A.第一象限 B.第二象限
 C.第三象限 D.第四象限
C.第三象限 D.第四象限
 答案:D
答案:D


 第37题. 若二次函数
第37题. 若二次函数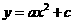 ,当x取x1,x2(x1≠x2)时,函数值相等,则当x取x1+x2时,函数值为( )
,当x取x1,x2(x1≠x2)时,函数值相等,则当x取x1+x2时,函数值为( )
 A.
A. B.
B.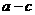 C.
C. D.
D.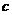
 答案:D
答案:D


 第38题. 二次函数
第38题. 二次函数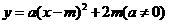 的顶点在( )
的顶点在( )
 A.
A.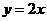 B.
B.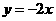 C.x轴上 D.y轴上
C.x轴上 D.y轴上
 答案:A
答案:A


 第39题. 关于二次函数
第39题. 关于二次函数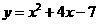 的最大(小)值,叙述正确的是( )
的最大(小)值,叙述正确的是( )
 A.当
A.当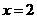 时,函数有最大值
时,函数有最大值
 B.当
B.当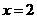 时,函数有最小值
时,函数有最小值
 C.当
C.当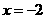 时,函数有最大值
时,函数有最大值
 D.当
D.当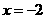 时,函数有最小值
时,函数有最小值
 答案:D
答案:D


 第40题. 若直线y=
第40题. 若直线y=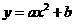 不经过第三,第四象限,则抛物线
不经过第三,第四象限,则抛物线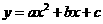 ( )
( )
 A.开口向上,对称轴是y轴
A.开口向上,对称轴是y轴
 B.开口向下,对称轴是y轴
B.开口向下,对称轴是y轴
 C.开口向上,对称轴平行于y轴
C.开口向上,对称轴平行于y轴
 D.开口向下,对称轴平行于y轴
D.开口向下,对称轴平行于y轴
 答案:C
答案:C


 第41题. 抛物线
第41题. 抛物线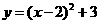 对称轴是( )
对称轴是( )
 A.直线
A.直线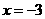 B.直线
B.直线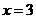 C.直线
C.直线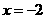 D.直线
D.直线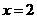
 答案:D
答案:D


 第42题. 已知函数
第42题. 已知函数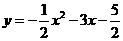 ,设自变量的值分别为x1,x2,x3,且-3< x1<
x2<x3,则对应的函数值的大小关系是( )
,设自变量的值分别为x1,x2,x3,且-3< x1<
x2<x3,则对应的函数值的大小关系是( )
 A.y3>y2>y1 B.y1>y3>y2
C.y2<y3<y1 D.y3<y2<y1
A.y3>y2>y1 B.y1>y3>y2
C.y2<y3<y1 D.y3<y2<y1
 答案:A
答案:A


 第43题. 下列关于抛物线
第43题. 下列关于抛物线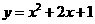 的说法中,正确的是( )
的说法中,正确的是( )
 A.开口向下 B.对称轴方程为x=1
A.开口向下 B.对称轴方程为x=1
 C.与x轴有两个交点 D.顶点坐标为(-1,0)
C.与x轴有两个交点 D.顶点坐标为(-1,0)
 答案:D
答案:D


 第44题. 函数
第44题. 函数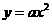 (a≠0)的图象与a的符号有关的是( )
(a≠0)的图象与a的符号有关的是( )
 A.对称轴 B.顶点坐标 C.开口方向 D.开口大小
A.对称轴 B.顶点坐标 C.开口方向 D.开口大小
 答案:C
答案:C


 第45题. 请你写出函数
第45题. 请你写出函数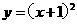 与
与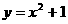 具有一个共同性质为__________.
具有一个共同性质为__________.
 答案:图象都是抛物线,开口向上,都有最低点(或最小值)
答案:图象都是抛物线,开口向上,都有最低点(或最小值)


 第46题. 试写出一个开口向上,对称轴为直线x=2,与y轴的交点的坐标为(0,3)的抛物线的解析式____________________.
第46题. 试写出一个开口向上,对称轴为直线x=2,与y轴的交点的坐标为(0,3)的抛物线的解析式____________________.
 答案:如
答案:如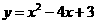 等
等


 第47题. 函数
第47题. 函数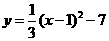 的图象可以通过
的图象可以通过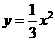 的图象向____移动______个单位,再向______移动____个单位后得到.
的图象向____移动______个单位,再向______移动____个单位后得到.
 答案:右,1,下,7
答案:右,1,下,7


 第48题. 已知二次函数
第48题. 已知二次函数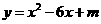 的最小值为1,那么m的值是
.
的最小值为1,那么m的值是
.
 答案:10
答案:10


 第49题. 由函数解析式画图象,一般按 、 、 三个步骤进行.
第49题. 由函数解析式画图象,一般按 、 、 三个步骤进行.
 答案:列表,描点,连线
答案:列表,描点,连线


 第50题. 已知抛物线l1:
第50题. 已知抛物线l1: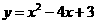
 (1)在平面直角坐标系中,画出抛物线
(1)在平面直角坐标系中,画出抛物线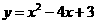 ,并求出抛物线l1的顶点关于y轴对称的点的坐标;
,并求出抛物线l1的顶点关于y轴对称的点的坐标;
 (2)已知抛物线l2与抛物线l1关于y轴对称,求抛物线l2的函数解析式.
(2)已知抛物线l2与抛物线l1关于y轴对称,求抛物线l2的函数解析式.
 答案:(1)图略,(-2,-1)
答案:(1)图略,(-2,-1)
 (2)
(2)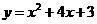


 第51题. 已知二次函数
第51题. 已知二次函数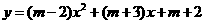 的图象过点(0,5).
的图象过点(0,5).
 (1)求m的值,并写出二次函数的解析式;
(1)求m的值,并写出二次函数的解析式;
 (2)求出二次函数图象的顶点坐标、对称轴
(2)求出二次函数图象的顶点坐标、对称轴
 答案:(1)m=3,则
答案:(1)m=3,则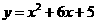
 (2)顶点坐标为(-3,-4),对称轴
(2)顶点坐标为(-3,-4),对称轴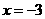


 第52题. 判断函数
第52题. 判断函数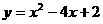 的图象是否经过第三象限?说明理由.
的图象是否经过第三象限?说明理由.
 答案:不经过第三象限,当
答案:不经过第三象限,当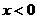 时,
时, 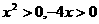 ,则
,则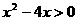 ,
,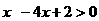 即
即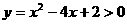 ,故当点
,故当点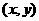 的横坐标
的横坐标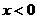 时,纵坐标y总是正数,也就是说横纵坐标不能同时为负数,因而该函数图象不可能经过第三象限
时,纵坐标y总是正数,也就是说横纵坐标不能同时为负数,因而该函数图象不可能经过第三象限


 第53题. 函数
第53题. 函数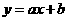 与
与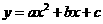 如图所示,则下列选项中正确的是( )
如图所示,则下列选项中正确的是( )

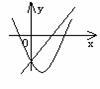 A.ab>0,c>0 B.ab<0,c>0
A.ab>0,c>0 B.ab<0,c>0
 C.ab>0,c<0 D.ab<0,c<0
C.ab>0,c<0 D.ab<0,c<0
 答案:D
答案:D



23.4二次函数与一元二次方程同步练习
第1题. 抛物线 与
与 轴有 个交点,因为其判别式
轴有 个交点,因为其判别式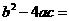 0,相应二次方程
0,相应二次方程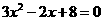 的根的情况为 .
的根的情况为 .
答案:
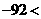 没有实数根.
没有实数根.
第2题. 函数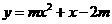 (
( 是常数)的图像与
是常数)的图像与 轴的交点个数为( )
轴的交点个数为( )
A.0个 B.1个 C.2个 D.1个或2个
答案:C
第3题. 关于二次函数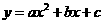 的图像有下列命题:①当
的图像有下列命题:①当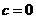 时,函数的图像经过原点;②当
时,函数的图像经过原点;②当 ,且函数的图像开口向下时,方程
,且函数的图像开口向下时,方程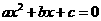 必有两个不相等的实根;③函数图像最高点的纵坐标是
必有两个不相等的实根;③函数图像最高点的纵坐标是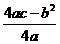 ;④当
;④当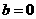 时,函数的图像关于
时,函数的图像关于 轴对称.
轴对称.
其中正确命题的个数是( )
A.1个 B.2个 C.3个 D.4个
答案:C
第4题. 关于 的方程
的方程 有两个相等的实数根,则相应二次函数
有两个相等的实数根,则相应二次函数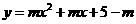 与
与 轴必然相交于 点,此时
轴必然相交于 点,此时 .
.
答案:一 4
第5题. 抛物线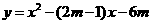 与
与 轴交于两点
轴交于两点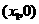 和
和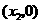 ,若
,若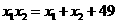 ,要使抛物线经过原点,应将它向右平移 个单位.
,要使抛物线经过原点,应将它向右平移 个单位.
答案:4或9
第6题. 关于 的二次函数
的二次函数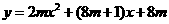 的图像与
的图像与 轴有交点,则
轴有交点,则 的范围是( )
的范围是( )
A.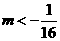 B.
B.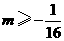 且
且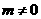 C.
C.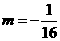 D.
D.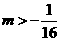 且
且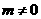
答案:B
第7题. 已知抛物线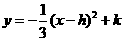 的顶点在抛物线
的顶点在抛物线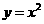 上,且抛物线在
上,且抛物线在 轴上截得的线段长是
轴上截得的线段长是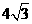 ,求
,求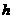 和
和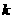 的值.
的值.
答案: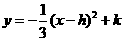 ,顶点
,顶点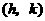 在
在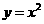 上,
上,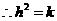 ,
,
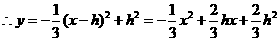 .
.
又它与 轴两交点的距离为
轴两交点的距离为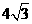 ,
,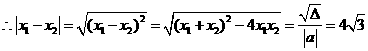 ,
,
求得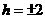 ,
, ,即
,即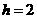 ,
, 或
或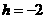 ,
, .
.
第8题. 已知函数 .
.
(1)求证:不论 为何实数,此二次函数的图像与
为何实数,此二次函数的图像与 轴都有两个不同交点;
轴都有两个不同交点;
(2)若函数 有最小值
有最小值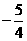 ,求函数表达式.
,求函数表达式.
答案:(1)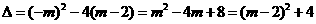 ,不论
,不论 为何值时,都有
为何值时,都有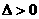 ,
,
此时二次函数图像与 轴有两个不同交点.
轴有两个不同交点.
(2)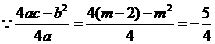 ,
,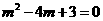 ,
,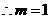 或
或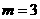 ,
,
所求函数式为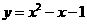 或
或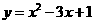 .
.
第9题. 下图是二次函数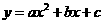 的图像,与
的图像,与 轴交于
轴交于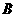 ,
,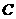 两点,与
两点,与 轴交于
轴交于 点.
点.
(1)根据图像确定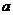 ,
,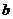 ,
,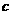 的符号,并说明理由;
的符号,并说明理由;
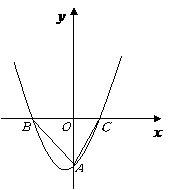 (2)如果
(2)如果 点的坐标为
点的坐标为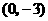 ,
,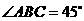 ,
,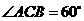 ,求这个二次函数的函数表达式.
,求这个二次函数的函数表达式.
答案:(1)抛物线开口向上,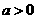 ;图像的对称轴在
;图像的对称轴在 轴左侧,
轴左侧,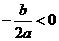 ,又
,又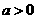 ,
,
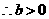 ;图像与
;图像与 轴交点在
轴交点在 轴下方,
轴下方,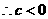 .
.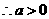 ,
,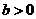 ,
, .
.
(2)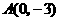 ,
,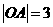 ,
,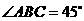 ,
,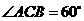 ,
,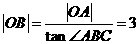 ,
,
 ,
,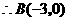 ,
,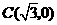 .设二次函数式为
.设二次函数式为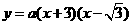 ,
,
把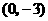 代入上式,得
代入上式,得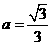 ,
, 所求函数式为
所求函数式为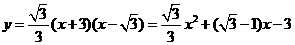 .
.
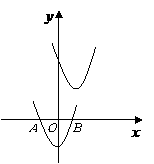
第10题. 已知抛物线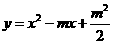 与抛物线
与抛物线 在直角坐标系中的位置如图所示,其中一条与
在直角坐标系中的位置如图所示,其中一条与 轴交于
轴交于 ,
,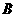 两点.
两点.
(1)试判断哪条抛物线经过 ,
,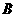 两点,并说明理由;
两点,并说明理由;
(2)若 ,
,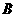 两点到原点的距离
两点到原点的距离 ,
,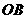 满足条件
满足条件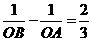 ,求经过
,求经过 ,
,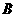 两点的这条抛物线的函数式.
两点的这条抛物线的函数式.
答案:(1)抛物线不过原点,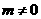 ,令
,令 ,
,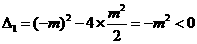 ,
,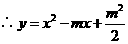 与
与 轴无交点,
轴无交点, 抛物线
抛物线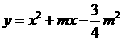 经过
经过 ,
,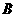 两点.
两点.
(2)设 ,
,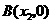 ,
,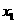 ,
,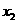 是方程
是方程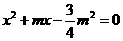 的两根
的两根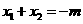 ,
,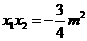 ,
, 在原点左边,
在原点左边,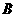 在原点右边,则
在原点右边,则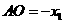 ,
,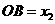 .
.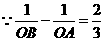 .
.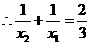 ,
,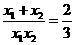 ,
,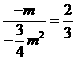 ,得
,得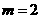 ,
, 所求函数式为
所求函数式为 .
.
第11题. 已知二次函数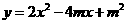 .
.
(1)求证:当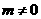 时,二次函数的图像与
时,二次函数的图像与 轴有两个不同交点;
轴有两个不同交点;
(2)若这个函数的图像与 轴交点为
轴交点为 ,
,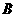 ,顶点为
,顶点为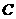 ,且△
,且△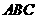 的面积为
的面积为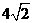 ,求此二次函数的函数表达式.
,求此二次函数的函数表达式.
答案:(1)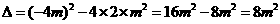 .
.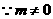 ,
,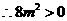 ,
,
 这个抛物线与
这个抛物线与 轴有两个不同交点.
轴有两个不同交点.
(2)设 ,
,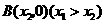 ,则
,则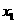 ,
,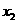 是方程
是方程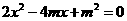 两根,
两根,
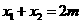 ,
,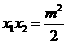 ,
,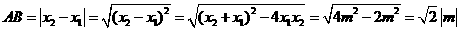 ,
,
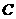 点纵坐标
点纵坐标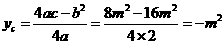 ,
,
 △
△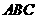 中
中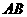 边上的高
边上的高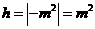 .
.
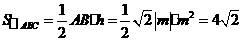 ,
,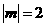 ,
,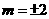 ,
,
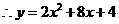 或
或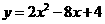 .
.
 第12题. 如图所示,函数
第12题. 如图所示,函数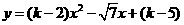 的图像与
的图像与 轴只有一个交点,则交点的横坐标
轴只有一个交点,则交点的横坐标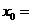 .
.
答案: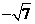
第13题. 已知抛物线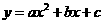 与
与 轴交于
轴交于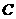 点,与
点,与 轴交于
轴交于 ,
,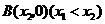 两点,顶点
两点,顶点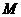 的纵坐标为
的纵坐标为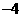 ,若
,若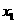 ,
,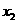 是方程
是方程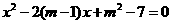 的两根,且
的两根,且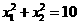 .
.
(1)求 ,
,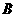 两点坐标;
两点坐标;
(2)求抛物线表达式及点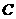 坐标;
坐标;
(3)在抛物线上是否存在着点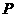 ,使△
,使△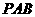 面积等于四边形
面积等于四边形 面积的2倍,若存在,求出
面积的2倍,若存在,求出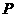 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
答案:(1)由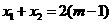 ,
,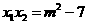 ,
,
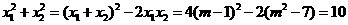 ,得
,得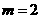 ,
,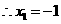 ,
,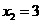 ,
,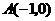 ,
,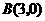 .
.
(2) 抛物线过
抛物线过 ,
,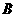 两点,其对称轴为
两点,其对称轴为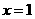 ,顶点纵坐标为
,顶点纵坐标为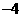 ,
, 抛物线为
抛物线为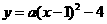 .
.
把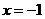 ,
,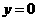 代入得
代入得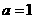 ,
, 抛物线函数式为
抛物线函数式为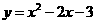 ,其中
,其中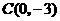 .
.
(3)存在着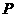 点.
点.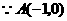 ,
,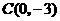 ,
,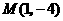 ,
,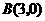 ,
,
 ,
,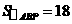 ,
,
即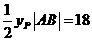 .
.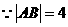 ,
,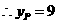 .把
.把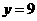 代入抛物线方程得
代入抛物线方程得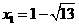 ,
,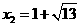 ,
,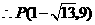 或
或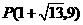 .
.
第14题. 二次函数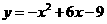 的图像与
的图像与 轴的交点坐标为 .
轴的交点坐标为 .
答案:(3,0)
第15题. 二次函数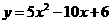 的图像与
的图像与 轴有 个交点.
轴有 个交点.
答案:0
第16题. 对于二次函数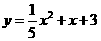 ,当
,当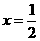 时,
时,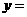 .
.
答案: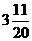
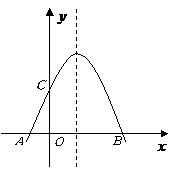 第17题. 如图是二次函数
第17题. 如图是二次函数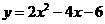 的图像,那么方程
的图像,那么方程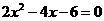 的两根之和 0.
的两根之和 0.
答案:
第18题. 求下列函数的图像与 轴的交点坐标,并作草图验证.
轴的交点坐标,并作草图验证.
(1)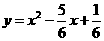 ; (2)
; (2)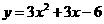 .
.
答案:(1)(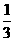 ,0),(
,0),( ,0),图略 (2)(1,0),(
,0),图略 (2)(1,0),(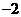 ,0),图略
,0),图略
第19题. 一元二次方程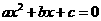 的两根为
的两根为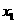 ,
,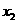 ,且
,且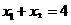 ,点
,点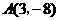 在抛物线
在抛物线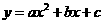 上,求点
上,求点 关于抛物线的对称轴对称的点的坐标.
关于抛物线的对称轴对称的点的坐标.
答案:(1,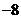 )
)
第20题. 若二次函数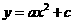 ,当
,当 取
取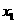 、
、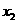 (
(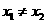 )时,函数值相等,则当
)时,函数值相等,则当 取
取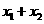 时,函数值为( )
时,函数值为( )
A.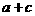 B.
B.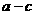 C.
C. D.
D.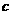
答案:D
第21题. 下列二次函数中有一个函数的图像与 轴有两个不同的交点,这个函数是( )
轴有两个不同的交点,这个函数是( )
A.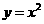 B.
B.
C.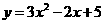 D.
D.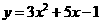
答案:D
第22题. 二次函数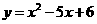 与
与 轴的交点坐标是( )
轴的交点坐标是( )
A.(2,0)(3,0) B.(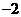 ,0)(
,0)(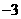 ,0) C.(0,2)(0,3) D.(0,
,0) C.(0,2)(0,3) D.(0,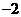 )(0,
)(0,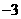 )
)
答案:A
第23题. 试说明一元二次方程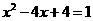 的根与二次函数
的根与二次函数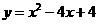 的图像的关系,并把方程的根在图象上表示出来.
的图像的关系,并把方程的根在图象上表示出来.
答案:一元二次方程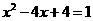 的根是二次函数
的根是二次函数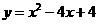 与直线
与直线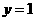 的交点的横坐标,图略.
的交点的横坐标,图略.
第24题. 利用二次函数图象求一元二次方程的近似根.
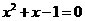
答案: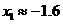 ,
,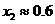
第25题. 利用二次函数图象求一元二次方程的近似根.
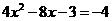
答案: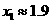 ,
,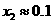
第26题. 函数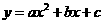 的图象如图所示,那么关于
的图象如图所示,那么关于 的一元二次方程
的一元二次方程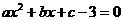 的根的情况是( )
的根的情况是( )
A.有两个不相等的实数根 B.有两个异号的实数根
C.有两个相等的实数根 D.没有实数根
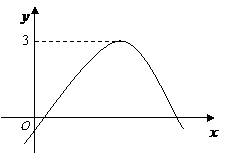
答案:C
第27题. 利用二次函数的图象求一元二次方程的近似值.
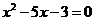
答案: ,
,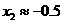
第28题. 抛物线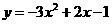 的图象与坐标轴交点的个数是( )
的图象与坐标轴交点的个数是( )
A.没有交点 B.只有一个交点
C.有且只有两个交点 D.有且只有三个交点
答案:A
第29题. 已知二次函数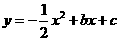 ,关于
,关于 的一元二次方程
的一元二次方程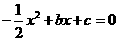 的两个实
的两个实
根是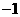 和
和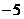 ,则这个二次函数的解析式为
,则这个二次函数的解析式为
答案: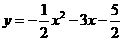
第30题. 已知二次函数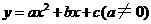 的顶点坐标
的顶点坐标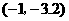 及部分图象(如图4所示),由图象可知关于
及部分图象(如图4所示),由图象可知关于 的一元二次方程
的一元二次方程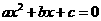 的两个根分别是
的两个根分别是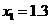 和
和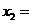 .
.
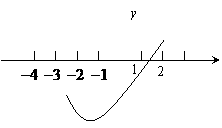
答案: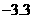
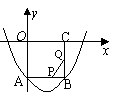
26.(12分)如图所示在平面直角坐标系xOy中,正方形OABC的边长为2cm,点
A、 C分别在y轴的负半轴和x的正半轴上,抛物线y=ax2+bx+c经过点A、B,
B、 且12a+5c=0,(1)求抛物线的解析式;
(2)如果点P由点A开始沿AB边以2cm/s的速度向点B移动,同时点Q由点B
开始沿BC边以1cm/s的速度向点C移动.移动开始后第t秒时,设S=PQ2(cm2),
试写出S与t 之间的函数关系,并写出t的取值范围及S的最大值和最小值;
25. (本小题满分12分)某电脑公司现有A,B,C三种型号的甲品牌电脑和D,E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.
(本小题满分12分)某电脑公司现有A,B,C三种型号的甲品牌电脑和D,E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.
 (1)
写出所有选购方案(利用树状图或列表方法表示); 如果各种选购方案被选中的可能性相同,那么A型号电脑被选中的概率是多少?
(1)
写出所有选购方案(利用树状图或列表方法表示); 如果各种选购方案被选中的可能性相同,那么A型号电脑被选中的概率是多少?
(2) 现知希望中学购买甲、乙两种品牌电脑共36台(价格如图所示),
恰好用了10万元人民币,其中甲品牌电脑为A型号电脑, 求购买
的A型号电脑有几台.
24. (12分)如图在矩形ABCD中,AB=1,AD=2,现将一块直径为2的半圆形纸片放置在矩形ABCD中,使其直径与AD重合,若将半圆上点D 固定,再把半圆往矩形外旋至A′D处,半圆弧A′D与AD交于点P, 设∠ADA′ =α
(12分)如图在矩形ABCD中,AB=1,AD=2,现将一块直径为2的半圆形纸片放置在矩形ABCD中,使其直径与AD重合,若将半圆上点D 固定,再把半圆往矩形外旋至A′D处,半圆弧A′D与AD交于点P, 设∠ADA′ =α
(1)若AP =2-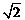 ,求α的度数;
,求α的度数;
(2)当∠α =30° 时,求阴影部分的面积
23.(12分)已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作
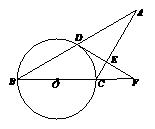 DE⊥AC于点E,交BC的延长线于点F.
DE⊥AC于点E,交BC的延长线于点F.
求证:(1)AD=BD; (2)DF是⊙O的切线.
21.(6分)化简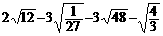 22.(6分)解方程:
22.(6分)解方程: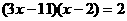
20.已知二次函数y=3(x-1)2+k的图象上有三个点A(1.5,y1,B(2, y2),C(-2.5, y3),
则y1, y2, y3,的大小关系为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com