
题目列表(包括答案和解析)
27.(本题满分10分)
在课外小组活动时,小慧拿来一道题(原问题)和小东、小明交流.
原问题:如图1,已知△ABC, ∠ACB=90° , ∠ABC=45°,分别以AB、BC为边向外作△ABD与△BCE, 且DA=DB, EB=EC,∠ADB=∠BEC=90°,连接DE交AB于点F. 探究线段DF与EF的数量关系.
小慧同学的思路是:过点D作DG⊥AB于G,构造全等三角形,通过推理使问题得解.
小东同学说:我做过一道类似的题目,不同的是∠ABC=30°,∠ADB=∠BEC=60°.
小明同学经过合情推理,提出一个猜想,我们可以把问题推广到一般情况.
请你参考小慧同学的思路,探究并解决这三位同学提出的问题:
(1)写出原问题中DF与EF的数量关系;
(2)如图2,若∠ABC=30°,∠ADB=∠BEC=60°,原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明;
(3)如图3,若∠ADB=∠BEC=2∠ABC, 原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请直接写出你的猜想不需证明.
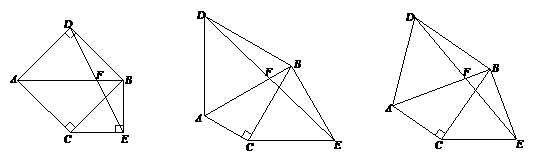
图1 图2 图3
26.(本题满分12分)探究规律:如图1,已知直线 ∥
∥ ,A、B为直线
,A、B为直线 上的两点,C、P为直线
上的两点,C、P为直线 上的两点。
上的两点。
(1)请写出图中面积相等的各对三角形: 。
(2)如果A、B、C为三个定点,点P在 上移动,那么无论P点移动到任何位置总有:
上移动,那么无论P点移动到任何位置总有:
与△ABC的面积相等;
理由是:
。



解决问题:
如图2,五边形ABCDE是张大爷十年前承包的一块土地的示意图,经过多年开垦荒地,现已变成如图3所示的形状,但承包土地与开垦荒地的分界小路(图3中折线CDE)还保留着,张大爷想过E点修一条直路,直路修好后,要保持直路左边的土地面积与承包时的一样多。请你用有关的几何知识,按张大爷的要求设计出修路方案。(不计分界小路与直路的占地面积)
(1)写出设计方案,并在图3中画出相应的图形;
(2)说明方案设计理由。
25.(本题满分10分)如图,在△ABC中,点O是AC边上的一个动点,过点O作MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OC=EF;
(2)当点O位于AC边的什么位置时,四边形AECF是矩形?并给出证明.

24.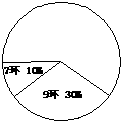 (本题满分10分)在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统计表(表1)和扇形统计图如下:
(本题满分10分)在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统计表(表1)和扇形统计图如下:
|
命中环数 |
10 |
9 |
8 |
7 |
||
|
命中次数 |
|
|
2 |
|
⑴ 根据统计表(图)中提供的信息,补全统计表及扇形统计图;
⑵ 已知乙运动员10次射击的平均成绩为9环,方差为1.2,如
果只能选一人参加比赛,你认为应该派谁去?并说明理由.
(参考资料: 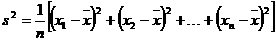 )
)
23.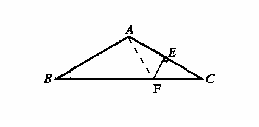 (本题满分10分)如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF.
(本题满分10分)如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF.
22.(本题满分8分)(1)有这样一个问题: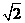 与下列哪些数相乘,结果是有理数?
与下列哪些数相乘,结果是有理数?
A.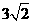 B.
B.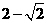 C.
C.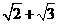 D.
D.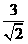 E.
E.
问题的答案是(只需填字母): ;
(2)如果一个数与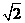 相乘的结果是有理数,则这个数的一般形式是什么(用代数式表示).
相乘的结果是有理数,则这个数的一般形式是什么(用代数式表示).
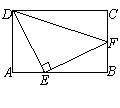
21.(本题满分8分)如图,矩形 中,点
中,点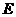 、
、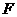 分别在
分别在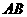 、
、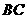 上,
上,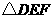 为等腰直角三角形,
为等腰直角三角形,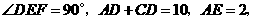 求
求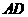 的长.
的长.
20.(本题满分8分)解方程
(1)8y2-2=4y(配方法)
(2)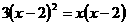
19.(本题满分8分)计算:
(1)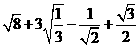 (2)
(2)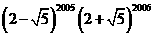
18.如图,正方形纸片ABCD的边长为1,M、N分别是AD、BC边上的点,将纸片的一角沿过点B的直线折叠,使A落在MN上,落点记为A′,折痕交AD于点E,若M、N分别是AD、BC边的中点,则A′N= ;
若M、N分别是AD、BC边的上距DC最近的n等分点(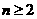 ,且n为整数),则A′N= (用含有n的式子表示)
,且n为整数),则A′N= (用含有n的式子表示)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com