4、已知α为锐角，tan(90°－α)=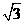，则α的度数为(　　　 )

　　 A．30°　　 B．45°　　 C．60°　　 D．75°

3、数据3、0、2、－1、1的中位数是　 (　　 )

A．2　 B．1　　 C．0　　 D．－1

2、下列运算正确的是(　　)

A.　x² ·x³ =x⁶　 　B. x²+x²=2x⁴ 　C.(-2x)² =4x²　 D.(-2x)² (-3x )³=6x⁵

1．一种病毒非常微小，其半径约为0.00000016m，用科学记数法可以表示为(　 )

　　 A．1.6×10⁶m　　　　　　　　　　 B．1.6×10^－6m

C．1.6×10^{－7m　　　　　　　　　　　 D}．1.6×10^－8m

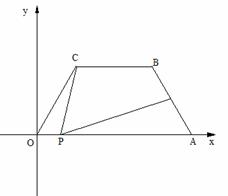
27.如图平面直角坐标中，四边形OABC是梯形，BC∥OA,OA=7，AB=OC=4，BC=3，

　 (1)求∠COA的度数；　　　　

　 (2)若P点在坐标轴上，且P、O、C三点构成等腰三角形，求P坐标；(只要写出坐标即可)

(3)在(2)中条件下,任取其中三点使经过该三点的图像是以y轴为对称轴的抛物线,称为最佳组合,求任取三点是最佳组合的概率.

(4)若有一个角是60°的三角板,60°角的顶点P在x轴上移动,三角板的60°角的一边经过C点,另一边与腰AB交与D ,问是否存在最大线段AD长度,如有求出最大值,且此时P点坐标,如没有,要说明理由.

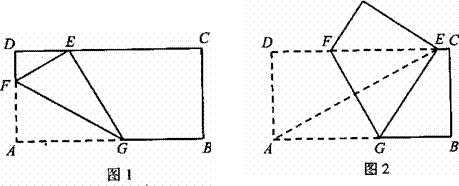
26.已知矩形纸片ABCD，AB=2，AD=1，将纸片折叠，使顶点A与边CD上的点E重合.

(1)如果折痕FG分别与AD、AB交于点F、G(如图1)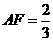，，求DE的长；

　(2)如果折痕FG分别与CD、AB交于点F、G(如图2)，△AED的外接圆与直线BC相切，

　 求折痕FG的长．

25．已知：将一副三角板(Rt△DEF)如图1摆放，点E、A、D、B在一条直线上，且D是AB的中点，将Rt△DEF绕点D顺时针方向旋转角α(0°<α<90°)．在旋转过程中，直线DE、AC相交于点M，直线DF、BC相交于点N，分别过点M、N作直线AB的垂线，垂足为G、H．

　　 (1)当α=30°时(如图2)，求证：AG=DH；

　　 (2)当α=60°时(如图3)，(1)中的结论是否成立？请写出你的结论，并说明理由；

(3)当0°<α<90°时(如图4)，(1)中的结论是否成立？请写出你的结论，并说明理由．

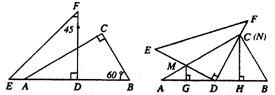
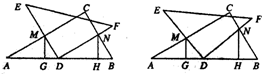
　　　　 图1　　　　　　　　 图2　　　　　　　 图3　　　　　　　　 图4

24．如图，足球场上守门员在处开出一高球，球从离地面1米的处飞出(在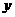轴上)，运动员乙在距点6米的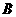处发现球在自己头的正上方达到最高点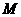，距地面约4米高，球落地后又一次弹起．据实验测算，足球在草坪上弹起后的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半．

(1)求足球开始飞出到第一次落地时，该抛物线的表达式．

(2)足球第一次落地点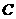距守门员多少米？(取)

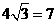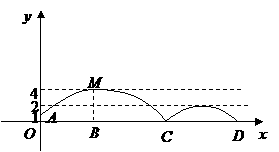(3)运动员乙要抢到第二个落点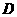，他应再向前跑多少米？(取)

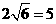23．B港在离观测站A的正北10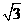海里处, 一艘轮船从B港出发向东航行.观测站第一次测得该船在A地北偏东30°的M处,半小时后测得该船在A地北偏东60°的N处,求这艘轮船的速度。

　　　　　　　　　　　　　　　　　　 北

22．今有甲，乙两人进行射击练习，成绩(命中环数)按先后次序记录如下：

试运用所学知识对甲，乙两人的成绩给予评判。(评判标准有三点以上者满分)