
题目列表(包括答案和解析)
3.下列函数图象的顶点坐标为(一2,一3)的是( )
A.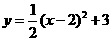 B.
B.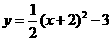
C. 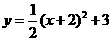 D.
D.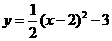
2.下列各点在抛物线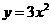 上的是( )
上的是( )
A.(O,3) B.(0,0)
C.(3,1) D.(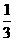 ,1)
,1)
1.下列方程中,是一元二次方程的是( )
A.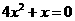 B.
B.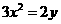 C.
C.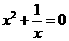 D.
D.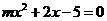
当 =-
=-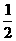 时,求代数式
时,求代数式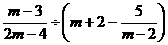 的值.
的值.
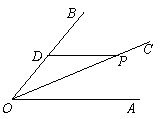 如图,OC是∠AOB的平分线,点P是OC上一点,过点P作PD∥OA交OB于点D,若∠AOB =60°,OD=6cm,求OP的长.
如图,OC是∠AOB的平分线,点P是OC上一点,过点P作PD∥OA交OB于点D,若∠AOB =60°,OD=6cm,求OP的长.
某商场店庆期间举办为期三天的“真情回报社会,购物(满188元)就送大礼”的幸运抽奖活动,共设五个奖金等级,最高奖金1万元,平均奖金180元.下面是商场公布的第一天活动情况统计表:
|
资金等级 |
一等奖 |
二等奖 |
三等奖 |
四等奖 |
五等奖 |
|
资金额(元) |
10000 |
5000 |
1000 |
50 |
10 |
|
中奖人数 |
3 |
8 |
89 |
300 |
600 |
一名顾客抽到一张奖券,奖金数为10元,她调查了周围不少正在兑奖的其他顾客,很少有超过50元的,她气愤地去找商场的领导理论,领导解释说这不存在什么欺骗,公布的统计表就是事实.
(1)若不超过50元为小奖,不低于1000元为大奖,请计算参加活动的顾客抽一张奖券获得小奖的概率;
(2)你认为商场所说的“平均奖金180元”是否欺骗了顾客?请通过计算说明理由;
(3)从第一天的活动情况分析:中奖金额的众数是______元;中位数是______元.“平均奖金180元”的说法能否反映中奖的一般金额?为什么?
如图,直线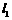 的解析表达式为
的解析表达式为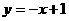 ,且
,且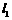 与x轴交于点B(-1,0),与y轴交于点D.l
与x轴交于点B(-1,0),与y轴交于点D.l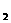 与y轴的交点为C(0,-2),直线l
与y轴的交点为C(0,-2),直线l 、l
、l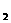 相交于点A,结合图像解答下列问题:
相交于点A,结合图像解答下列问题:
(1)求△ADC的面积;
(2)求直线l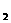 表示的一次函数的解析式;
表示的一次函数的解析式;
 (3)当x为何值时,l
(3)当x为何值时,l 、l
、l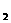 表示的两个函数的函数值都大于0.
表示的两个函数的函数值都大于0.
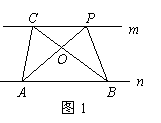 (1)如图1,已知:直线m∥n,A、B为直线n上两点,C、P为直线m上两点.请写出图中,△ABC和△ABP面积之间的数量关系:
;
(1)如图1,已知:直线m∥n,A、B为直线n上两点,C、P为直线m上两点.请写出图中,△ABC和△ABP面积之间的数量关系:
;
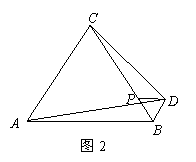 (2)如图2,边长为6的正三角形ABC,P是BC边上一点,且PB=1,以PB为一边作正三角形PBD,则△ADC的面积为 ;
(2)如图2,边长为6的正三角形ABC,P是BC边上一点,且PB=1,以PB为一边作正三角形PBD,则△ADC的面积为 ;
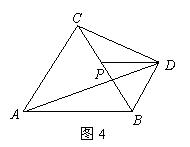
(3)如图3,边长为6的正三角形ABC,P是BC边上一点,且PB=2,以PB为一边作正三角形PBD,则△ADC的面积为 ;
(4)根据上述计算的结果,你发现了怎样的规律?
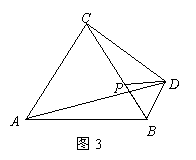
提出自己的猜想并依据图4予以证明。
(5)如图5,有一块正三角形的草皮ABC,由于某种原因,需要将三角形草皮ABE移植到三角形的草皮AEC的右侧,成为一块新的三角形草皮ADC(A、E、D三点要在一条直线上),并保持其面积不变,请你画图说明如何确定点D的位置.

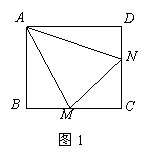
已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.当∠MAN绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.
(1)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.
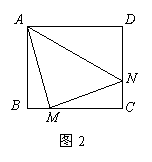
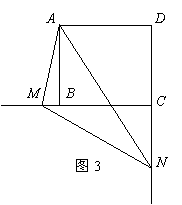
 (2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的数量关系?并说明理由.
(2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的数量关系?并说明理由.
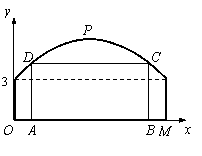
如图,某隧道横截面的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成,最大高度为6米,底部宽度为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.
(1)直接写出点M及抛物线顶点P的坐标;
(2)求出这条抛物线的函数解析式;
(3)若要搭建一个矩形“支撑架”AD-DC-CB,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长的最大值是多少?
如图,在矩形ABCD中,AB=3cm,BC=4cm.设P,Q分别为BD,BC上的动点,点P自点D沿DB方向作匀速移动的同时,点Q自点B沿BC方向向点C作匀速移动,移动的速度均为1cm/s,设P,Q移动的时间为t(0≤t≤4).
(1)当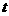 为何值时,PQ⊥BC?
为何值时,PQ⊥BC?
|
|
|
 (3)当
(3)当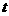 为何值时,△PBQ为等腰三角形?
为何值时,△PBQ为等腰三角形?

|
 |
||||||
|
|||||||
17. 如图,在△ABC中,∠C=90°,∠B=25°,以点C为圆心,
如图,在△ABC中,∠C=90°,∠B=25°,以点C为圆心,
AC为半径的圆交AB于点D,则︿AD的度数为 .
|
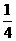 ,则口袋里绿球的个数为 个。
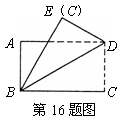
,则口袋里绿球的个数为 个。16.如图所示,矩形纸片ABCD,AB=2,∠ADB=30°,沿对角线BD折叠(使△ABD和△EBD落在同一平面内),则A、E两点间的距离为 .
15. 抛物线
抛物线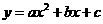 过点A(1,0),B(3,0),则此抛物线的对称轴是直线
过点A(1,0),B(3,0),则此抛物线的对称轴是直线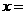 .
.
14.已知点P在第二象限,且到x轴的距离是4,到y轴的距离是3,则点P的坐标为 .
13.已知: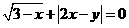 ,那么
,那么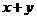 的值为 .
的值为 .
12.据媒体报道,我国因环境污染造成的巨大经济损失每年高达680 000 000元,这个数用科学记数法表示为 元.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com