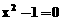1．方程的解为　　　　　　　　 。

26．(12分)已知抛物线(m为常数)经过点(0，4)

⑴求m的值；

⑵将该抛物线先向右、再向下平移得到另一条抛物线。已知这条平移后的抛物线满足下述两个条件：它的对称轴(设为直线l₂)与平移前的抛物线的对称轴(设为l₁)关于y轴对称；它所对应的函数的最小值为－8.

①试求平移后的抛物线所对应的函数关系式；

②试问在平移后的抛物线上是否存在着点P，使得以3为半径的⊙P既与x轴相切，又与直线l₂相交？若存在，请求出点P的坐标，并求出直线l₂被⊙P所截得的弦AB的长度；若不存在，请说明理由。

25. (本题满分10分)．如图1，在四边形ABCD中，已知AB=BC＝CD，∠BAD和∠CDA均为锐角，点P是对角线BD上的一点，PQ∥BA交AD于点Q，PS∥BC交DC于点S，四边形PQRS是平行四边形。

(1)当点P与点B重合时，图1变为图2，若∠ABD＝90°，求证：△ABR≌△CRD；

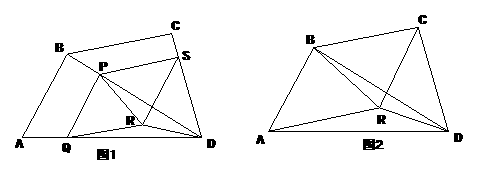
(2)对于图1，若四边形PRDS也是平行四边形，此时，你能推出四边形ABCD还应满足什么条件？

23．(本小题满分8分)在物理试验中，当电流在一定

时间段内正常通过电子元件时每个电子元件的状

态有两种可能：通电或断开，并且这两种状态的可

能性相等．

(1)如图23-1，当只有一个电子元件时，之

间电流通过的概率是　　　　　 ．

(2)如图23-2，当有两个电子元件并联时，

请你用树状图(或列表法)表示图中之间电

流能否通过的所有可能情况，求出之间电

流通过的概率；

(3)如图23-3，当有三个电子元件并联时，请你

猜想之间电流通过的概率是　　　　　 ．

2 4．(本题满分10分)某工厂生产的某种产品按质量分为1 0个档次．第1档次(最低档次)的产品一天能生产7 6件，每件利润10元．每提高一个档次，每件利润增加2元，但一天产量减少4件．

　　 (1)若生产第x档次的产品一天的总利润为y元(其中x为正整数，且1≤x≤10)，求出y关于x的函数关系式；

(2)若生产第x档次的产品一天的总利润为1080元，求该产品的质量档次．

22．(本题满分8分)数学老师将本班学生的身高数据(精确到l厘米)交给甲、乙两同学，要求他们各自独立地绘制一幅频数分布直方图．甲绘制的如图①所示，乙绘制的如图②所示，经确认，甲绘制的图是正确的，乙在整理数据与绘图过程中均有个别错误．

请回答下列问题：

　　 (1)该班学生有多少人?

　　 (2)甲同学身高为1 6 5厘米，他说：“我们班上比我高的人不超过1/4”．他的说法正确吗?说明理由．

　　 (3)写出乙同学在整理或绘图过程中的错误(写出一个即可)．

　　 (4)设该班学生的身高数据的中位数为a，试写出a的值

21．(本小题满分8分)如图7，是直角边长等于的等腰

直角三角形，是直径为的圆．图8是选择基本图形

用尺规画出的图案：．

(1)请你以图7的图形为基本图形，按给定图形的大小设

计画一个新图案，还要选择恰当的图形部分涂上阴影，并

直接写出其面积(尺规作图，不写作法，保留痕迹，作直

角三角形时可使用三角板)．

(2)请你写出一句在解答本题的过程中体会最深且与数

学有关的话．

20．(5分)如图，在电线杆里地面6米高的C处向

地面拉缆绳，缆绳和地面成63°角，求缆绳AC

的长(精确到0.01米)

19．(本小题满分5分)计算：–2²++(–2007)⁰– 4sin45°．

18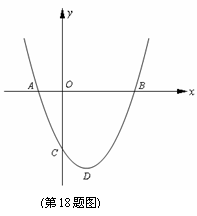．如图，二次函数y=ax²+bx+c(a≠0).图象的顶点为D，

其图象与x轴的交点A、B的横坐标分别为–1、3，与y

轴负半轴交于点C.下面四个结论：①2a+b=0；

②a+b+c>0；③只有当a= 时，△ABD是等腰直角三

角形；④使△ACB为等腰三角形的a的值可以有三个.

那么，其中正确的结论是　　　　　　 .(只填你

认为正确结论的序号)

　 (注：二次函数y=ax²+bx+c(a≠0)图象的顶点坐

标为(– ，))

17.在中，，(如图16)．如果圆的半

径为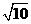，且经过点，那么线段的长等于　　　　 ．