4.任给一些不同的实数n，得到不同的抛物线y=2x²+n，如当n=0，±2时，关于这些抛物线有以下结论：①开口方向都相同；②对称轴都相同；③形状都相同；④都有最低点，其中判断正确的个数是

A.1个　 　　　　 　　　B.2个　 　　　 　　　C.3个　　　　　　　 D.4个

3.不论m取任何实数，抛物线y=a(x+m)²+m(a≠0)的顶点都

A.在y=x直线上　　　　　　　　　　　　　 B.在直线y=－x上

C.在x轴上　　　　　　　　　　　　　　　 D.在y轴上

2.抛物线y=－2x²－x+1的顶点在第_____象限

A.一　 　　 　　　　B.二　 　　　　　 　　　C.三　　 　　　 　　D.四

1.函数y=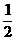x²+2x+1写成y=a(x－h)²+k的形式是

A.y=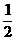(x－1)²+2　　　　　　　　　　　　 B.y=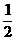(x－1)²+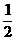

C.y=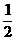(x－1)²－3　　　　　　　　　　　　　　 D.y=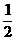(x+2)²－1

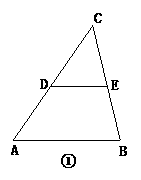
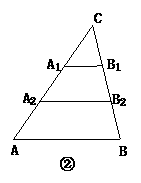
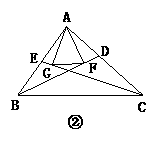
18．(2004·江苏南通)(13分)已知：△ABC中，AB=10．

　　 (1)如图①，若点D，E分别是AC，BC边的中点，求DE的长；

　　 (2)如图②，若点A₁，A₂把AC边三等分，过A₁，A₂作AB边的平行线，分别交BC边于点B₁，B₂，求A₁B₁+A₂B₂的值；

　　 (3)如图③，若点A₁，A₂，…，A₁₀把AC边十一等分，过各点作AB边的平行线，分别交BC边于点B₁，B₂，…，B₁₀．根据你所发现的规律，直接写出A₁B₁+A₂B₂+…+A₁₀B₁₀的结果．

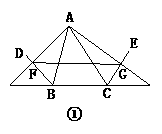
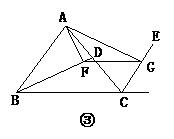
17．(开放题)(12分)已知：如图27-3-45①所示，BD、CE分别是△ABC的外角平分线，过点A作AF⊥BD，AG⊥CE，垂足分别为F、G．连结FG，延长AF、AG，与直线BC相交，易证FG=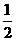(AB+BC+AC)．若(1)BD、CE分别是△ABC的内角平分线(如图②)；(2)BD为△ABC的内角平分线，CE为△ABC的外角平分线(如图③)，则在图②、图③两种情况下，线段FG与△ABC三边又有怎样的数量关系？请写出你的猜想，并对其中的一种情况给予证明．

新课标理念中考题(满分13分)

16．(自主探究题)(10分)等腰梯形ABCD中，AD∥BC，E、F、G、H分别是AD、BE、BC、CE的中点．试探究：

　　 (1)四边形EFGH的形状；

(2)若BC=2AD，且梯形ABCD的面积为9，求四边形EFGH的面积．

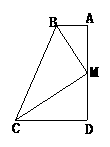
15．(创新实践题)(11分)已知：如图所示，梯形ABCD中，AB∥CD，且AB+CD=BC，M是AD的中点，求证：BM⊥CM．

14．(创新情景题)如图所示，直角梯形ABCD的中位线EF的长为a，垂直于底的腰AB的长为b，则图中阴影部分的面积等于_________．

新课标拓展训练(满分33分)

13．(应用题)如图所示，要测量A、B两点间的距离，在O点设桩，取OA中点C，OB中点D，测得CD=31.4m，则AB=__________m．