
题目列表(包括答案和解析)
2.圆既是 对称图形,又是 对称图形;它的对称中心是 ,对称轴是 ,
有 条对称轴。
1.确定一个圆有两要素,一是 ,二是 ,圆心确定 、半径确定 ;
(1)掌握圆的有关性质和计算
① 弧、弦、圆心角之间的关系:
在同圆或等圆中,如果两条劣弧(优弧)、两条两个圆心角中有一组量对应相等,那么它们所对应的其余各组量也分别对应相等.
② 垂径定理: 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
垂径定理的推论:
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
弦的垂直平分线经过圆心,并且平分弦所对的两条弧.
平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
③ 在同一圆内,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半.
④ 圆内接四边形的性质:
圆的内接四边形对角互补,并且任何一个外角等于它的内对角.
(2)点与圆的位置关系
①
设点与圆心的距离为 ,圆的半径为
,圆的半径为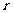 ,
,
则点在圆外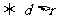 ; 点在圆上
; 点在圆上 ; 点在圆内
; 点在圆内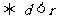 .
.
② 过不在同一直线上的三点有且只有一个圆. 一个三角形有且只有一个外接圆.
③ 三角形的外心是三角形三边垂直平分线的交点.
三角形的外心到三角形的三个顶点的距离相等.
(3)直线与圆的位置关系
① 设圆心到直线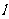 的距离为
的距离为 ,圆的半径为
,圆的半径为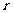 ,
,
则直线与圆相离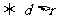 ;直线与圆相切
;直线与圆相切 ;直线与圆相交
;直线与圆相交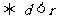 .
.
② 切线的性质:与圆只有一个公共点;
圆心到切线的距离等于半径;圆的切线垂直于过切点的半径.
③ 切线的识别:如果一条直线与圆只有一个公共点,那么这条直线是圆的切线.
到圆心的距离等于半径的直线是圆的切线.
经过半径的外端且垂直与这条半径的直线是圆的切线.
④ 三角形的内心是三角形三条内角平分线的交点.
三角形的内心到三角形三边的距离相等.
⑤ 切线长:圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长.
⑥ 切线长定理:从圆外一点引圆的两条切线,它们的切线长相等.
这一点和圆心的连线平分这两条切线的夹角.
(4)圆与圆的位置关系
① 圆与圆的位置关系有五种:外离、外切、相交、内切、内含.
设两圆心的距离为 ,两圆的半径为
,两圆的半径为 ,则两圆外离
,则两圆外离
两圆外切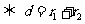
两圆相交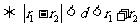
两圆内切
两圆内含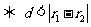
② 两个圆构成轴对称图形,连心线(经过两圆圆心的直线)是对称轴.
由对称性知:两圆相切,连心线经过切点. 两圆相交,连心线垂直平分公共弦.
③ 两圆公切线的定义:和两个圆都相切的直线叫做两圆的公切线.
两个圆在公切线同旁时,这样的公切线叫做外公切线.
两个圆在公切线两旁时,这样的公切线叫做内公切线.
④ 公切线上两个切点的距离叫做公切线的长.
(5)与圆有关的计算
①
弧长公式: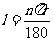 扇形面积公式:
扇形面积公式: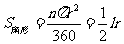
(其中为 圆心角的度数,
圆心角的度数,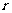 为半径)
为半径)
② 圆柱的侧面展开图是矩形.
圆柱体也可以看成是一个矩形以矩形的一边为轴旋转而形成的几何体.
圆柱的侧面积=底面周长×高
圆柱的全面积=侧面积+2×底面积
③ 圆锥的侧面展开图是扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
圆锥体可以看成是由一个直角三角形以一条直角边为轴旋转而成的几何体.
④
圆锥的侧面积= ×底面周长×母线;圆锥的全面积=侧面积+底面积
×底面周长×母线;圆锥的全面积=侧面积+底面积
能力锻炼与提升(一)-- 圆中的有关概念和性质
3.1圆
第1题. 若一个点到圆心的距离恰好等于半径,则此点必在 ;若一个点到圆心的距离大于半径,则此点必在 ;若一个点到圆心的距离小于半径,则此点必在 .
答案:圆上 圆外 圆内
第2题.  的直径为12,
的直径为12,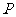 为一个点,当
为一个点,当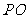 为 时,
为 时,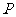 点在圆上;当
点在圆上;当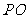 时,
时,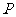 点在圆内;当
点在圆内;当 时,
时,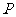 点必在 .
点必在 .
答案:6  圆外
圆外
第3题. 以长为 的已知线段
的已知线段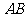 为一条边,面积是
为一条边,面积是 的△
的△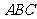 的另一个顶点
的另一个顶点 的轨迹是 .
的轨迹是 .
答案:平行于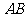 且与
且与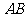 距离为
距离为 的点的直线
的点的直线
第4题. 和已知线段两个端点相等的点的轨迹是 .
答案:已知线段的垂直平分线
第5题. 在Rt△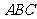 中,
中, ,
, ,
, ,若以
,若以 为圆心,以5为半径作
为圆心,以5为半径作 ,则点
,则点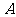 在
在 ,点
,点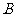 在
在 ;若以
;若以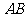 为直径作
为直径作 ,则点
,则点 在
在 .
.
答案:上 外 上
第6题. 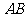 是
是 的弦,
的弦, 于
于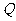 ,再以
,再以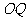 为半径作同心圆,称作小
为半径作同心圆,称作小 ,点
,点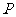 是
是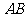 上异于
上异于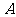 ,
,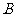 ,
,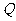 的任意一点,则
的任意一点,则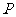 点位置是( )
点位置是( )
A.在大 上 B.在大
上 B.在大 外部
外部
C.在小 内部 D.在小
内部 D.在小 外而大
外而大 内
内
答案:D
第7题. 如图, ,
, 是
是 的两条直径.
的两条直径.
求证:四边形 为矩形.
为矩形.
答案: ,
,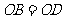 ,
, 四边形
四边形 为平行四边形.又
为平行四边形.又 ,
, 为矩形.
为矩形.
第8题. 如图,菱形 的对角线
的对角线 和
和 相交于
相交于 点,
点, ,
,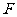 ,
, ,
, 分别是
分别是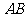 ,
, ,
, ,
, 的中点,求证:
的中点,求证: ,
,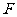 ,
, ,
, 四个点在以
四个点在以 为圆心的同一个圆上.
为圆心的同一个圆上.

答案:连结 ,
, ,
,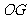 ,
,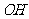 .
. 四边形
四边形 为菱形,
为菱形, ,且
,且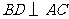 .
. ,
, ,
, ,
, 分别为
分别为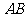 ,
, ,
, ,
, 的中点,
的中点, ,
, ,
,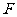 ,
, ,
, 四点在以
四点在以 为圆心,
为圆心,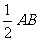 为半径的圆上.
为半径的圆上.
第9题. 等腰梯形 中,
中,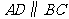 ,求证
,求证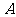 ,
,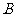 ,
, ,
,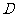 四个顶点共圆.
四个顶点共圆.
答案:分别作等腰梯形两腰的垂直平分线,交于点 根据等腰梯形对称性知,
根据等腰梯形对称性知, 点必在等腰梯形的对称轴上.根据线段垂直平分线和对称轴性质得
点必在等腰梯形的对称轴上.根据线段垂直平分线和对称轴性质得 ,故
,故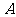 ,
,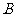 ,
, ,
,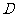 四点必在以
四点必在以 为圆心,
为圆心, 为半径的圆上.
为半径的圆上.
第10题. 菱形四边的中点到 的距离相等,因此菱形各边的中点在以 为圆心,以 为半径的圆上.
答案:对角线的交点,对角线的交点,四边中点到对角线交点距离
 第11题. 画边长为3cm的正方形
第11题. 画边长为3cm的正方形 ,连结
,连结 ,
, 相交于点
相交于点 ,以点
,以点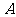 为圆心,
为圆心,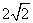 cm长为半径画圆,试判断点
cm长为半径画圆,试判断点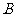 ,
, ,
,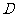 ,
, 四点与这个圆的位置关系.
四点与这个圆的位置关系.
答案:外,外,外,内
第12题. 生活中有许多由圆组成的图案,请你用圆规等作图工具设计一个美丽图案.
答案:略
第13题. 已知等腰 (如图),试取斜边
(如图),试取斜边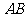 上的一点为圆心画图,使点
上的一点为圆心画图,使点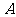 ,
,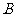 ,
, 分别在所画的圆内、圆外和圆上.
分别在所画的圆内、圆外和圆上.

答案:作中线 ,则
,则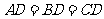 ,且
,且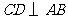 .在
.在 上任取一点
上任取一点 ,连接
,连接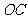 .以
.以 为圆心,
为圆心, 为半径画圆,这个
为半径画圆,这个 即符合要求.这是因为
即符合要求.这是因为 (垂线段最短),所以点
(垂线段最短),所以点 在
在 内.
内. (三角形两边之和大于第三边),所以点
(三角形两边之和大于第三边),所以点 在
在 外.
外.
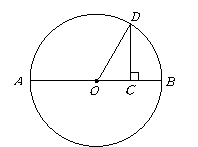 第14题. 如图,已知半径为
第14题. 如图,已知半径为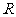 的半圆
的半圆 ,过直径
,过直径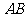 上一点
上一点 ,作
,作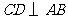 交半圆于点
交半圆于点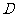 ,且
,且 ,试求
,试求 的长.
的长.
答案:(1)当 点在
点在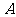 、
、 之间时,如图甲.
之间时,如图甲.
由勾股定理 ,故
,故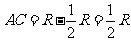
(2)当 点在
点在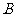 、
、 之间时,如图乙.
之间时,如图乙.
 由勾股定理知
由勾股定理知 ,故
,故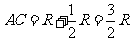
第15题. 如图,在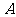 地往北60m的
地往北60m的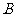 处有一幢民房,西80m的
处有一幢民房,西80m的 处有一变电设施,在
处有一变电设施,在 的中点
的中点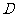 处有一古建筑.因施工需要必须在
处有一古建筑.因施工需要必须在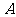 处进行一次爆破,为使民房、变电设施、古建筑都不遭到破坏,问爆破影响面的半径应控制在什么范围内?
处进行一次爆破,为使民房、变电设施、古建筑都不遭到破坏,问爆破影响面的半径应控制在什么范围内?

答案:小于50m
第16题.  的面积为
的面积为 ,
, 所在的平面内有一点
所在的平面内有一点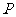 ,当
,当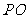 时,点
时,点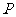 在
在 上;当
上;当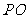 时,点
时,点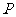 在
在 内;当
内;当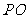 时,点
时,点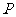 在
在 外.
外.
答案:
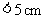
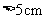
第17题. 如图,墙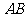 与墙
与墙 垂直,在地面的
垂直,在地面的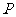 处有一木柱,系着一匹马,已知系马的绳子的长度为
处有一木柱,系着一匹马,已知系马的绳子的长度为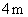 ,试在图中画出马的活动区域.
,试在图中画出马的活动区域.
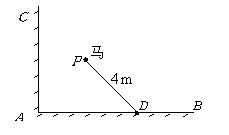
答案:以 为圆心,图中线段长为半径画一条与两墙均相交的弧.
为圆心,图中线段长为半径画一条与两墙均相交的弧.
第18题. 如图,矩形 的对角线
的对角线 与
与 相交于点
相交于点 ,试说明点
,试说明点 ,
, ,
, 在以
在以 为圆心、
为圆心、 的长为半径的
的长为半径的 上.
上.

答案:由矩形的性质得 ,故点
,故点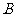 ,
, ,
,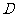 都在以
都在以 为圆心、
为圆心、 为半径的圆上.
为半径的圆上.
第19题. 如图,在图中用图形(阴影)表示到定点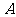 的距离小于或等于
的距离小于或等于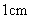 的所有点组成的图形.
的所有点组成的图形.

答案:如图所示,图中的阴影部分(包括边界)即为所求.

下列命题中正确的是__________. [ ]
A.点的轨迹是一个图形
B.点的轨迹是符合某一条件的点组成的图形
C.点的轨迹是符合某一条件的所有的点所组成的图形
9. 已知线段BC, 以BC为底边的等腰三角形的顶点A的轨迹是________.
8. 以已知线段为斜边的直角三角形的直角顶点的轨迹是_________.
7.和⊙O相交于圆上两点A、B的圆的圆心的轨迹是__________.
6. 已知点A,经过点A,且半径长等于2cm的圆的圆心轨迹是__________.
5. 到点O的距离等于5cm的点的轨迹是________________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com