
题目列表(包括答案和解析)
7.已知二次函数y=x2-2(m-1)x+m2-2m-3的图象与函数y=-x2+6x的图象交于y 轴一点,则m=_______.
5.二次函数y=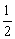 x2+3x+
x2+3x+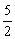 的图象是由函数y=
的图象是由函数y=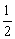 x2的图象先向_____平移____个单位,再向_____平移_____个单位得到的.
x2的图象先向_____平移____个单位,再向_____平移_____个单位得到的.
 6.已知二次函数y=mx2+(m-1)x+m-1的图象有最低点,且最低点的纵坐标是零,则m=_______.
6.已知二次函数y=mx2+(m-1)x+m-1的图象有最低点,且最低点的纵坐标是零,则m=_______.
4.如果函数y=(k-3)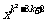 +kx+1是二次函数,则k的值一定是_______.
+kx+1是二次函数,则k的值一定是_______.
3.二次函数y=ax2+bx+c中,a>0,b<0,c=0,则其图象的顶点是在第_____象限.
2.二次函数y=2x2+bx+c的顶点坐标是(1,-2),则b=_____,c=_____.
1.二次函数y=3x2-2x+1的图象是开口方向_______,顶点是________, 对称轴是__________.
23.3二次函数y=ax2+bx+c的图象和性质同步练习
第31题. (济宁课改)二次函数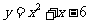 的图象与
的图象与 轴交点的横坐标是( )
轴交点的横坐标是( )
A.2和 B.
B. 和
和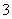 C.2和3 D.
C.2和3 D. 和
和
答案:A
第32题. (荆州课改)已知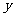 关于
关于 的函数:
的函数: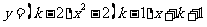 中满足
中满足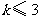 .
.
(1)求证:此函数图象与 轴总有交点.
轴总有交点.
(2)当关于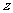 的方程
的方程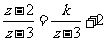 有增根时,求上述函数图象与
有增根时,求上述函数图象与 轴的交点坐标.
轴的交点坐标.
答案:(1)当 时,函数为
时,函数为 ,图象与
,图象与 轴有交点.
轴有交点.
当 时,
时,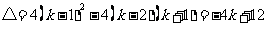
当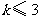 时,
时, ,此时抛物线与
,此时抛物线与 轴有交点.
轴有交点.
因此,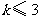 时,
时,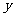 关于
关于 的函数
的函数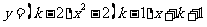 的图象与
的图象与 轴总有交点.
轴总有交点.
(2)关于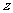 的方程去分母得:
的方程去分母得: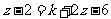 ,
,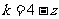 .
.
由于原分式方程有增根,其根必为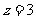 .这时
.这时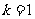 (6分)
(6分)
这时函数为 .它与
.它与 轴的交点是
轴的交点是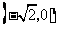 和
和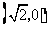
第33题. (苏州课改)抛物线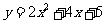 的对称轴是
的对称轴是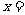 ______.
______.
答案: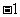
 第34题. (安徽课改)抛物线
第34题. (安徽课改)抛物线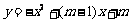 与
与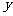 轴交于
轴交于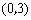 点.
点.
(1)求出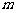 的值并画出这条抛物线;
的值并画出这条抛物线;
(2)求它与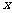 轴的交点和抛物线顶点的坐标;
轴的交点和抛物线顶点的坐标;
(3)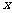 取什么值时,抛物线在
取什么值时,抛物线在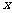 轴上方?
轴上方?
(4)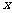 取什么值时,
取什么值时,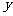 的值随
的值随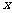 值的增大而减小?
值的增大而减小?
[解]
答案:解:(1)由抛物线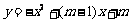 与
与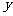 轴交于
轴交于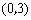 ,得:
,得: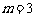 .
.
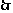 抛物线为
抛物线为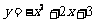 .图象略.
.图象略.
(2)由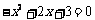 ,得
,得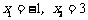 .
.
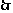 抛物线与
抛物线与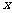 轴的交点为
轴的交点为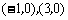 .
.
 ,
,
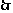 抛物线顶点坐标为
抛物线顶点坐标为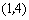 .
.
(3)由图象可知:
当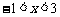 时,抛物线在
时,抛物线在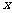 轴上方.
轴上方.
(4)由图象可知:
当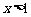 时,
时,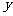 的值随
的值随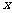 值的增大而减小.
值的增大而减小.
第35题. (贺州课改)已知抛物线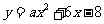 与直线
与直线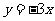 相交于点
相交于点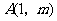 .
.
(1)求抛物线的解析式;
(2)请问(1)中的抛物线经过怎样的平移就可以得到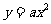 的图象?
的图象?
(3)设抛物线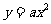 上依次有点
上依次有点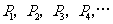 ,其中横坐标依次是
,其中横坐标依次是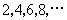 ,纵坐标依次为
,纵坐标依次为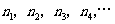 ,试求
,试求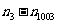 的值.
的值.
答案:解:(1) 点
点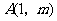 在直线
在直线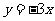 上,
上,
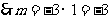 .
.
把 代入
代入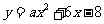 ,
,
得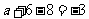 .求得
.求得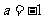 .
.
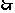 抛物线的解析式是
抛物线的解析式是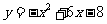 .
.
(2) .
.
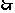 顶点坐标为
顶点坐标为 .
.
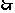 把抛物线
把抛物线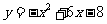 向左平移3个单位长度得到
向左平移3个单位长度得到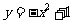 的图象,再把
的图象,再把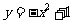 的图象向下平移1个单位长度得到
的图象向下平移1个单位长度得到 的图象.
的图象.
(3)由题意知, 的横坐标是连续偶数,所以
的横坐标是连续偶数,所以 的横坐标是
的横坐标是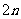 ,纵坐标为
,纵坐标为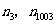 所对应的纵坐标依次是
所对应的纵坐标依次是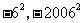 .
.

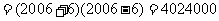 .
.
第36题. (湖南永州非课改)观察下列四个函数的图象( )
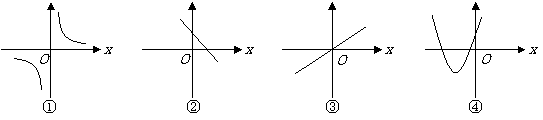
将它们的序号与下列函数的排列顺序:正比例函数、一次函数、二次函数、反比例函数,对应正确的是( )
A.①②③④ B.②③①④ C.③②④① D.④②①③
答案:C
第37题. (沈阳非课改)抛物线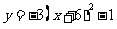 的对称轴是直线( )
的对称轴是直线( )
A.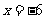 B.
B.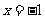 C.
C.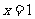 D.
D.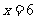
答案:A
第38题. (兰州A课改)请选择一组你喜欢的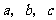 的值,使二次函数
的值,使二次函数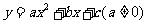 的图象同时满足下列条件:①开口向下,②当
的图象同时满足下列条件:①开口向下,②当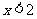 时,
时,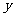 随
随 的增大而增大;当
的增大而增大;当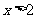 时,
时,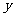 随
随 的增大而减小.这样的二次函数的解析式可以是 .
的增大而减小.这样的二次函数的解析式可以是 .
答案:答案不唯一,只要满足对称轴是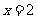 ,
,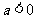 .
.
第39题. (兰州A课改)已知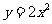 的图象是抛物线,若抛物线不动,把
的图象是抛物线,若抛物线不动,把 轴,
轴,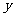 轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是( ).
轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是( ).
A.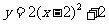 B.
B.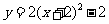
C.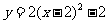 D.
D.
答案:B
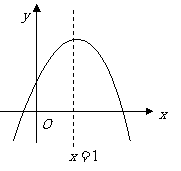
第40题. (兰州A课改)已知二次函数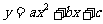 的图象如图所示,对称轴是
的图象如图所示,对称轴是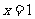 ,则下列结论中正确的是( ).
,则下列结论中正确的是( ).
A.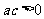 B.
B.
C.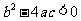 D.
D.
答案:D
第41题. (辽宁十一市课改)已知二次函数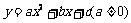 ,其中
,其中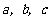 满足
满足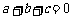 和
和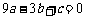 ,则该二次函数图象的对称轴是直线 .
,则该二次函数图象的对称轴是直线 .
答案: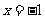
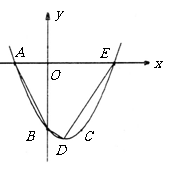
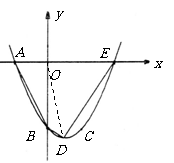
第42题. (辽宁十一市非课改)如图,已知抛物线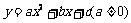 经过
经过 ,
,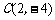 三点,且与
三点,且与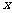 轴的另一个交点为
轴的另一个交点为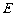 .
.
(1)求抛物线的解析式;
(2)用配方法求抛物线的顶点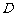 的坐标和对称轴;
的坐标和对称轴;
(3)求四边形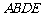 的面积.
的面积.
答案:解:(1) 抛物线
抛物线 经过
经过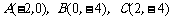 三点
三点
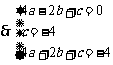 解得
解得
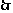 抛物线解析式:
抛物线解析式: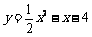 .
.
(2)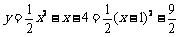
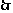 顶点坐标
顶点坐标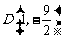 ,对称轴:
,对称轴: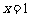 .
.
(3)连结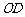 ,对于抛物线解析式
,对于抛物线解析式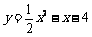
当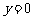 时,得
时,得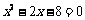 ,解得:
,解得: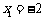 ,
,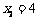
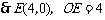
 .
.
第43题. (浙江湖州课改)已知二次函数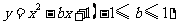 ,当
,当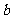 从
从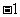 逐渐变化到
逐渐变化到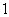 的过程中,它所对应的抛物线位置也随之变动.下列关于抛物线的移动方向的描述中,正确的是( )
的过程中,它所对应的抛物线位置也随之变动.下列关于抛物线的移动方向的描述中,正确的是( )
A.先往左上方移动,再往左下方移动 B.先往左下方移动,再往左上方移动
C.先往右上方移动,再往右下方移动 D.先往右下方移动,再往右上方移动
答案:C
第44题. (江西课改)二次函数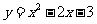 的最小值是 .
的最小值是 .
答案:
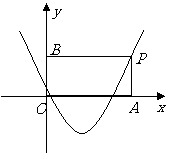
第45题. (长春课改)如图,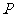 为抛物线
为抛物线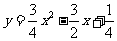 上对称轴右侧的一点,且点
上对称轴右侧的一点,且点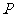 在
在 轴上方,过点
轴上方,过点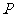 作
作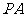 垂直
垂直 轴于点
轴于点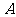 ,
,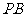 垂直
垂直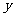 轴于点
轴于点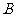 ,得到矩形
,得到矩形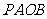 .若
.若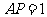 ,求矩形
,求矩形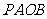 的面积.
的面积.
答案: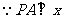 轴,
轴,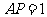 ,
,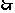 点
点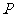 的纵坐标为
的纵坐标为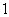 .
.
当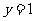 时,
时, ,即
,即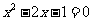 .
.
解得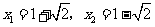 .
.
 抛物线的对称轴为
抛物线的对称轴为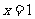 ,点
,点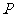 在对称轴的右侧,
在对称轴的右侧,
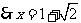 .
.
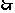 矩形
矩形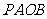 的面积为
的面积为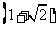 个平方单位.
个平方单位.
第46题. 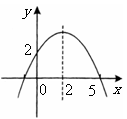 (山西非课改)二次函数
(山西非课改)二次函数 的图象如图所示.
的图象如图所示.
有下列结论:①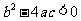 ;②
;②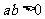 ;③
;③ ;④
;④ ;⑤当
;⑤当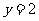 时,
时, 只能等于
只能等于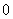 .其中正确的是( )
.其中正确的是( )
A.①④ B.③④ C.②⑤ D.③⑤
答案:B
第47题. (威海非课改)抛物线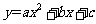
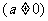 过点
过点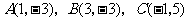 ,顶点为
,顶点为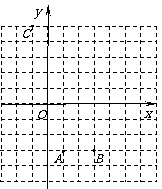 M点.
M点.
(1)求该抛物线的解析式.
(2)试判断抛物线上是否存在一点P,使∠POM=90˚.
若不存在,说明理由;若存在,求出P点的坐标.
(3)试判断抛物线上是否存在一点K,使∠OMK=90˚,
说明理由.
答案:解:(1)根据题意,得
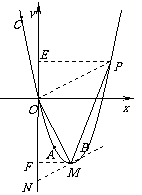
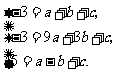
解,得 
∴
抛物线的解析式为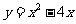 .
.
(2)抛物线上存在一点P,使∠POM=90˚.
x=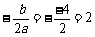 ,
,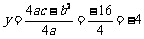 .
.
∴ 顶点M的坐标为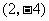 .
.
设抛物线上存在一点P,满足OP⊥OM,其坐标为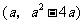 .
.
过P点作PE⊥y轴,垂足为E;过M点作MF⊥y轴,垂足为F.
则 ∠POE+∠MOF=90˚,∠POE+∠EPO=90˚.
∴ ∠EPO=∠FOM.
∵ ∠OEP=∠MFO=90˚,
∴ Rt△OEP∽Rt△MFO.
∴ OE∶MF=EP∶OF.
即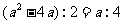 .
.
解,得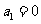 (舍去),
(舍去),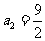 .
.
∴ P点的坐标为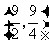 .
.
(3)过顶点M作MN⊥OM,交y轴于点N.则 ∠FMN+∠OMF=90˚.
∵ ∠MOF+∠OMF=90˚,
∴ ∠MOF=∠FMN.
又∵ ∠OFM=∠MFN=90˚,
∴ △OFM∽△MFN.
∴ OF∶MF=MF∶FN. 即 4∶2=2∶FN.∴ FN=1.
∴ 点N的坐标为(0,-5).
设过点M,N的直线的解析式为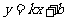 .
.
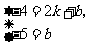 解,得
解,得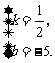 直线的解析式为
直线的解析式为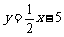 .
.
∴ 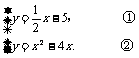 把①代入②,得
把①代入②,得 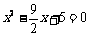 .
.
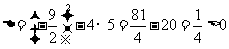 .
.
∴ 直线MN与抛物线有两个交点(其中一点为顶点M).
∴ 抛物线上必存在一点K,使∠OMK=90˚.
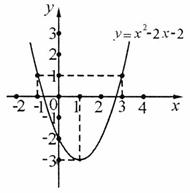
第48题. (资阳课改)已知函数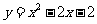 的图象如图3所示,根据其中提供的信息,可求得使
的图象如图3所示,根据其中提供的信息,可求得使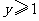 成立的
成立的 的取值范围是( )
的取值范围是( )
A.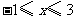 B.
B.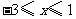
C. D.
D.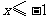 或
或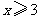
答案:D
第49题. (安徽非课改)请你写出一个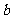 的值,使得函数
的值,使得函数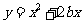 在第一象限内
在第一象限内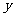 的值随着
的值随着 的值增大而增大,则
的值增大而增大,则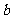 可以是 .
可以是 .
答案:答案不唯一,如0;1;2等
第50题. (南充课改)二次函数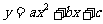 中,
中,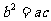 ,且
,且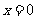 时
时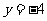 ,则( )
,则( )
A.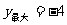 B.
B.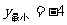 C.
C.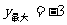 D.
D.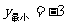
答案:C
第51题. (徐州非课改)下表给出了代数式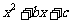 与
与 的一些对应值:
的一些对应值:
 |
… |
0 |
1 |
2 |
3 |
4 |
… |
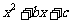 |
… |
3 |
|
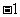 |
|
3 |
… |
(1)请在表内的空格中填入适当的数;
(2)设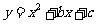 ,则当
,则当 取何值时,
取何值时, ?
?
(3)请说明经过怎样平移函数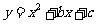 的图象得到函数
的图象得到函数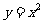 的图象.
的图象.
答案:(1)0,0;
(2)当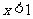 或
或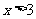 时,
时, .(写出
.(写出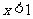 或
或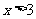 中的一个得1分)
中的一个得1分)
(用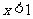 和
和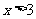 中的特殊值说明得1分,只用
中的特殊值说明得1分,只用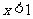 或
或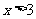 中的特殊值说明不得分)
中的特殊值说明不得分)
(3)由(1)得 ,即
,即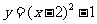 ,
,
将抛物线 先向左平移2个单位(1分),再向上平移1个单位(1分)即得抛物线
先向左平移2个单位(1分),再向上平移1个单位(1分)即得抛物线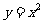 .
.
(配方正确,并说明将抛物线 的顶点移到原点得2分;不配方,但说明将抛物线
的顶点移到原点得2分;不配方,但说明将抛物线 的顶点
的顶点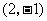 移到原点得2分;不配方,只说明将抛物线的顶点移到原点不得分)
移到原点得2分;不配方,只说明将抛物线的顶点移到原点不得分)
第52题. (龙岩三县非课改)已知抛物线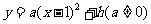 与
与 轴交于
轴交于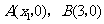 两点,则线段
两点,则线段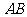 的长度为( )
的长度为( )
A.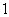 B.
B.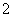 C.
C.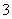 D.
D.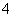
答案:D

第53题. (岳阳课改)小明从右边的二次函数 图象中,观察得出了下面的五条信息:
图象中,观察得出了下面的五条信息:
① ,②
,②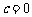 ,③函数的最小值为
,③函数的最小值为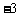 ,④当
,④当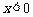 时,
时,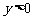 ,⑤当
,⑤当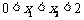 时,
时, .你认为其中正确的个数为( )
.你认为其中正确的个数为( )
A.2 B.3
C.4 D.5
答案:C
8、如图,已知Rt△ABC中,∠B=900,∠A=600,AB=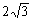 cm.点O从C点出发,沿CB以每秒1cm的速度向B点方向运动,运动到B点时运动停止.当点O运动了t秒(t>0)时,以O点为圆心的圆与边AC相切于点D,与BC边所在直线相交于E、F两点.过E作EG⊥DE交直线AB于G,连结DG.
cm.点O从C点出发,沿CB以每秒1cm的速度向B点方向运动,运动到B点时运动停止.当点O运动了t秒(t>0)时,以O点为圆心的圆与边AC相切于点D,与BC边所在直线相交于E、F两点.过E作EG⊥DE交直线AB于G,连结DG.
(1)求BC的长;
(2)若E与B不重合,问t为何值时,△BEG与△DEG相似?
(3)试问:当t在什么范围内时,点G在线段BA的延长线上?当t在什么范围内时,点G在线段AB的延长线上?
(4)当点G在线段AB上(不包括端点A、B)时,求四边形ADEG的面积S(cm2)关于O点运动时间t(秒)的函数关系式,并问点O运动了几秒时,S取得最大值?最大值为多少?
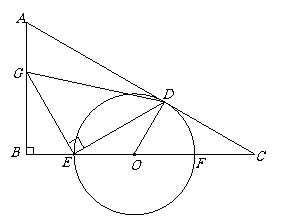
7、已知:如图,点D是以AB为直径的圆O上任意一点,且不与点A、B重合,点C是弧BD的中点,过C作CE∥AB,交AD或其延长线于E,连结BE交AC于G.
(1)求证:AE=CE;
(2)若过点C作CM⊥AD交AD的延长线于点M, 试说明:MC与⊙O相切;
(3)若CE=7,CD=6,求EG的长.

6、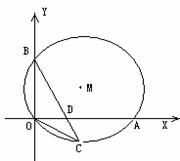 如图:⊙M经过O点,并且与x轴、y轴分别交于A、B两点,线段OA,OB(OA﹥OB)的长是方程x2-17x+60=0的两根。
如图:⊙M经过O点,并且与x轴、y轴分别交于A、B两点,线段OA,OB(OA﹥OB)的长是方程x2-17x+60=0的两根。
(1)求线段OA、OB的长;(2)已知点C在劣弧OA上,连结BC交OA于D,当OC2=CD×CB时,求点C的坐标;(3)在(2)的条件下,在⊙M上是否存在一点P,使⊿POD的面积=⊿ABD的面积?若存在,求出点P的坐标,若不存在,说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com