
题目列表(包括答案和解析)
2. 4 证明(2)同步练习
4 证明(2)同步练习
 考标要求1能用角平分线的性质和等腰三角形的性质、判定解有关几何问题
考标要求1能用角平分线的性质和等腰三角形的性质、判定解有关几何问题
 2 继续了解证明的基本步骤和书写格式,培养推理意识和表达能力。
2 继续了解证明的基本步骤和书写格式,培养推理意识和表达能力。
 重点:用角平分线的性质和等腰三角形的性质、判定证明有关几何问题证明有关几何问题
重点:用角平分线的性质和等腰三角形的性质、判定证明有关几何问题证明有关几何问题

 难点:用角平分线的性质和等腰三角形的性质、判定解决实际问题
难点:用角平分线的性质和等腰三角形的性质、判定解决实际问题
 一 选择题(每小题5分,共25分)
一 选择题(每小题5分,共25分)
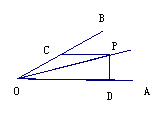
 1如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD等于( )
1如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD等于( )
 A
4 B 3 D 2 C 1
A
4 B 3 D 2 C 1

|
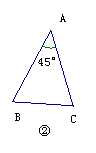 2 如图,在下列三角形中,若AB=AC,则能被
2 如图,在下列三角形中,若AB=AC,则能被

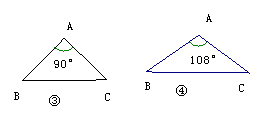
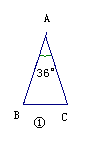 一条直线分成两个小等腰三角形的是( )
一条直线分成两个小等腰三角形的是( )

|

|
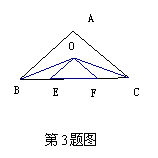
 ∠ABC、∠ACB的平分线相交于O,OE∥AB交BC于E,
∠ABC、∠ACB的平分线相交于O,OE∥AB交BC于E,
 OF∥AC,交BC于F,则图中等腰三角
OF∥AC,交BC于F,则图中等腰三角
 形有( )
形有( )
 A 6 B 5 C 4 D 3
A 6 B 5 C 4 D 3
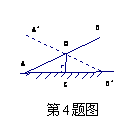
 4 同学们都玩过跷跷板的游戏,如图,
4 同学们都玩过跷跷板的游戏,如图,
 是一个跷跷板的示意图,立柱OC与地面
是一个跷跷板的示意图,立柱OC与地面
 垂直,OA=OB,当跷跷板的一头着地时,
垂直,OA=OB,当跷跷板的一头着地时,
 ∠OAC=25°,则当跷跷板的另一头B着地时
∠OAC=25°,则当跷跷板的另一头B着地时
 ∠AOA’等于( )
∠AOA’等于( )
 A
2 5° B 50 °C 60° D 130°
A
2 5° B 50 °C 60° D 130°
 5如图,AC平分∠BAD,CM⊥AB,且AB+AD=2AM,那么∠ADC与∠ABC( )
5如图,AC平分∠BAD,CM⊥AB,且AB+AD=2AM,那么∠ADC与∠ABC( )
 A
相等 B 互补 C 和为150° D 和为165°
A
相等 B 互补 C 和为150° D 和为165°










 二填空题(每小题5分,共25分)
二填空题(每小题5分,共25分)
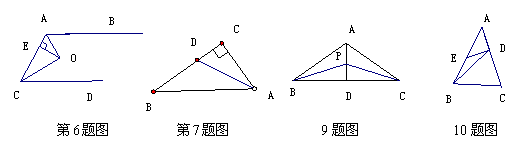
 6 如图,已知:AB∥CD,
6 如图,已知:AB∥CD,
 ∠BAC与∠ACD的平分线交于点O,OE⊥AC于E,且OE=2cm,则AB、CD间的距离是________.
∠BAC与∠ACD的平分线交于点O,OE⊥AC于E,且OE=2cm,则AB、CD间的距离是________.

 7 如图,已知,∠C=90°,AD平分∠BAC,点D到AB的距离是3cm,则DC=_____cm
7 如图,已知,∠C=90°,AD平分∠BAC,点D到AB的距离是3cm,则DC=_____cm
 8 (2007年杭州)一个等腰三角形的一个外角等于110°,则这个三角形的三个角应该是
8 (2007年杭州)一个等腰三角形的一个外角等于110°,则这个三角形的三个角应该是
 _____________________________________
_____________________________________
 9 如图,已知△ABC中,∠ABC与
9 如图,已知△ABC中,∠ABC与
 ∠ACB的平分线的交点P恰好在BC边
∠ACB的平分线的交点P恰好在BC边
 的高AD上,那么△ABC一定是__________三角形
的高AD上,那么△ABC一定是__________三角形
 10 如图,△ABC中,AB=AC,点D
10 如图,△ABC中,AB=AC,点D
 在AC上,点E在AB上,且AD=DE=EB,
在AC上,点E在AB上,且AD=DE=EB,
 BD=BC,那么∠A=___°.
BD=BC,那么∠A=___°.








 三 解答题(每小题10分,共50分)
三 解答题(每小题10分,共50分)

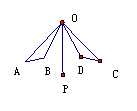 11已知:如图,OP是∠AOC和∠BOD的平分线,OA=OC,OB=OD。
11已知:如图,OP是∠AOC和∠BOD的平分线,OA=OC,OB=OD。
 求证:AB=CD。
求证:AB=CD。
|






 12 如图 AF是△ABC的角平分线,BD⊥AF,交AF的延长线于D,DE∥AC交AB于E,,求证:AE=BE
12 如图 AF是△ABC的角平分线,BD⊥AF,交AF的延长线于D,DE∥AC交AB于E,,求证:AE=BE


|






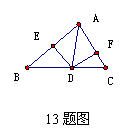
 13 如图,△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积为33
13 如图,△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积为33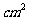 , AB=10cm,AC=12cm,求DF的长。
, AB=10cm,AC=12cm,求DF的长。








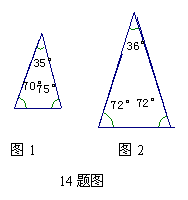
 14 如图,现在给出两个三角形,请你把图1分割成两个等腰三角形,把图2分割成三个等腰三角形。
14 如图,现在给出两个三角形,请你把图1分割成两个等腰三角形,把图2分割成三个等腰三角形。












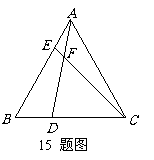 15 (2007年乐山)如图,在等边
15 (2007年乐山)如图,在等边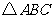 中,点
中,点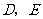 分别在边上,且
分别在边上,且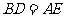 ,
,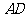 与
与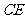 交于点
交于点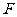 .
.
 (1)求证:
(1)求证: ;
;
 (2)求
(2)求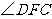 的度数.
的度数.


























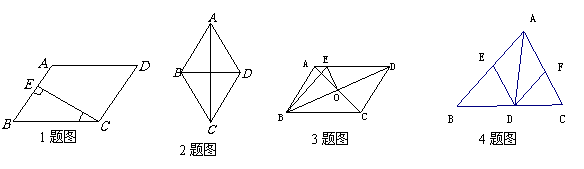
4. (2007连云港)如图,在△ABC中,点E,D,F分别在边
(2007连云港)如图,在△ABC中,点E,D,F分别在边
 AB,BC、CA上,且DE∥CA,DF∥BA。下列四个判断中,
AB,BC、CA上,且DE∥CA,DF∥BA。下列四个判断中,
 不正确的是( )
不正确的是( )
 A.四边形AEDF是平行四边形
A.四边形AEDF是平行四边形
 B.如果∠BAC =90°,那么四边形AEDF是矩形
B.如果∠BAC =90°,那么四边形AEDF是矩形
 C.如果AD平分∠BAC,那么四边形AEDF是菱形
C.如果AD平分∠BAC,那么四边形AEDF是菱形

 D.如果AD⊥BC且AB=AC,那么四边形AEDF是菱形
D.如果AD⊥BC且AB=AC,那么四边形AEDF是菱形







 5 在△ABC中,DE是中位线,∠B的平分线交DE于F,则△ABF
5 在△ABC中,DE是中位线,∠B的平分线交DE于F,则△ABF
 一定是( )
一定是( )
 A 锐角三角形 B 直角三角形
A 锐角三角形 B 直角三角形
 C 钝角三角形 D直角三角形 或钝角三角形
C 钝角三角形 D直角三角形 或钝角三角形
 二 填空题(每小题5分,共25分)
二 填空题(每小题5分,共25分)
 6 △ABC与平行四边形ABCD如图放置,点D、G分别在边AB、AC
6 △ABC与平行四边形ABCD如图放置,点D、G分别在边AB、AC
 上,点E、F在边BC上,已知BE=DE,CF=FG,则∠A的度数是_____
上,点E、F在边BC上,已知BE=DE,CF=FG,则∠A的度数是_____
 7如图,平行四边形ABCD中,点E在AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F,若△FDE的周长为10,△FCB的周长为24,则FC的长为_______
7如图,平行四边形ABCD中,点E在AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F,若△FDE的周长为10,△FCB的周长为24,则FC的长为_______

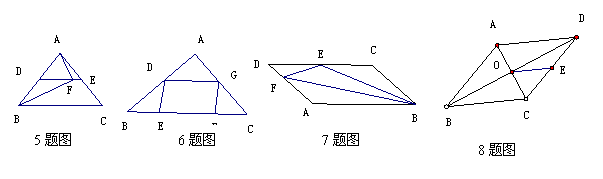 8如图,在菱形ABCD中,对角线AC、BD相交于点O,E为BC中, 则与OE相等的线段有____________________
8如图,在菱形ABCD中,对角线AC、BD相交于点O,E为BC中, 则与OE相等的线段有____________________







 9 如图,矩形ABCD中,AB=2
9 如图,矩形ABCD中,AB=2 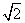 ,将∠D与∠C分别
,将∠D与∠C分别

 沿着过A和B的直线AE、AF向内折叠,使点D、C重合
沿着过A和B的直线AE、AF向内折叠,使点D、C重合
 于点G,且∠EGF=∠AGB,则AD=________.
于点G,且∠EGF=∠AGB,则AD=________.
 10 如图,有一块边长为4的正方形塑料模板ABCD,将一块足够大的直角三角板的直角落在A点,两直角边分别与CD交于点F,与CB的延长线交于点E,则四边形AECF的面积是___________
10 如图,有一块边长为4的正方形塑料模板ABCD,将一块足够大的直角三角板的直角落在A点,两直角边分别与CD交于点F,与CB的延长线交于点E,则四边形AECF的面积是___________
 三 解答题(12×3+14=50)
三 解答题(12×3+14=50)
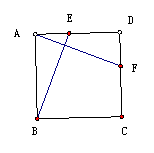
 11(2007年哈尔滨)已知:如图,点E为正方形ABCD的边AD上一点,连接BE,过点A作AH⊥BE,垂足为H,延长AH交CD于点F。求证:DE=CF
11(2007年哈尔滨)已知:如图,点E为正方形ABCD的边AD上一点,连接BE,过点A作AH⊥BE,垂足为H,延长AH交CD于点F。求证:DE=CF

|









 12 四边形ABCD中,AB=a,CD=b(a>b),M、N分别是AD、BC的中点,求MN的取值范围
12 四边形ABCD中,AB=a,CD=b(a>b),M、N分别是AD、BC的中点,求MN的取值范围
|











 13 (2007青岛
)将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′ 处,折痕为EF.
13 (2007青岛
)将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′ 处,折痕为EF.
 (1)求证:△ABE≌△AD′F;
(1)求证:△ABE≌△AD′F;

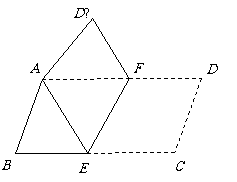 (2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论.
(2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论.
|












 14(2007年徐州)如图,过四边形ABCD的四个顶点分别作对角线AC、BD的平行线,所围成的四边形EFGH显然是平行四边形。
14(2007年徐州)如图,过四边形ABCD的四个顶点分别作对角线AC、BD的平行线,所围成的四边形EFGH显然是平行四边形。
 (1)当四边形ABCD分别是菱形、矩形、等腰梯形时,相应的平行四边形EFGH一定是“菱形、矩形、正方形”中的哪一种?请将你的结论填入下表:
(1)当四边形ABCD分别是菱形、矩形、等腰梯形时,相应的平行四边形EFGH一定是“菱形、矩形、正方形”中的哪一种?请将你的结论填入下表:
|
四边形ABCD |
菱形 |
矩形 |
等腰梯形 |
|
平行四边形EFGH |
|
|
|
(2)反之,当用上述方法所围成的平行四边形EFGH分别是矩形、菱形时,相应的原四边形ABCD必须满足怎样的条件?
 解:
解:











2. 4 证明(3)同步练习
4 证明(3)同步练习
 考标要求
考标要求
 1 能有综合法证明与平行四边形的性质、判定以及三角形中位线有关的问题,体会严谨证明的必要性。2 进一步培养表达能力。
1 能有综合法证明与平行四边形的性质、判定以及三角形中位线有关的问题,体会严谨证明的必要性。2 进一步培养表达能力。
 一 填空题
一 填空题
 一 填空题(每小题5分,共25分)
一 填空题(每小题5分,共25分)
 1 (2007乐山)如图(1),在平面四边形
1 (2007乐山)如图(1),在平面四边形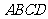 中,
中,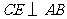 ,
,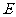 为垂足.如果
为垂足.如果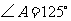 ,则
,则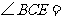 ( )
( )
 A.
A.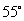 B.
B.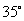 C.
C.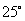 D.
D.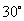
 2(2007嘉兴)如图,在菱形ABCD中,不一定成立的是( )
2(2007嘉兴)如图,在菱形ABCD中,不一定成立的是( )
 (A)四边形ABCD是平行四边形(B)AC⊥BD
(A)四边形ABCD是平行四边形(B)AC⊥BD
 (C)△ABD是等边三角形 (D)∠CAB=∠CAD
(C)△ABD是等边三角形 (D)∠CAB=∠CAD
 3(2007日照)如图,在周长为20cm的□ABCD中,AB≠AD,
3(2007日照)如图,在周长为20cm的□ABCD中,AB≠AD,
 AC、BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为
AC、BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为
 (A)4cm (B)6cm
(A)4cm (B)6cm
 (C)8cm (D)10cm
(C)8cm (D)10cm
2. 4 证明(4) 同步练习
4 证明(4) 同步练习
 考标要求
考标要求
 1 体会反正法的含义,掌握三角形外心的性质。
1 体会反正法的含义,掌握三角形外心的性质。
 2巩固综合法证题的能力,
2巩固综合法证题的能力,
 重点:培养演绎推理的能力 ;难点:利用反证法的证题思想。
重点:培养演绎推理的能力 ;难点:利用反证法的证题思想。
 一 选择题(每小题5分共25分)
一 选择题(每小题5分共25分)
 1 直角三角形斜边上的中点是( )
1 直角三角形斜边上的中点是( )
 A 三条边中线的交点 B 三边高线的交点,
A 三条边中线的交点 B 三边高线的交点,
 C三个角平分线的交点D 三边中垂线的交点
C三个角平分线的交点D 三边中垂线的交点
 2(2007长沙)如图,已知等腰梯形
2(2007长沙)如图,已知等腰梯形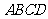 中,
中,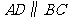 ,
,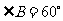 ,
,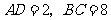 ,则此等腰梯形的周长为( )
,则此等腰梯形的周长为( )
 A.19 B.20
A.19 B.20
 C.21 D.22
C.21 D.22
 3 Rt△中,∠C=90°,AB垂直平分线交直线BC于D ,若
3 Rt△中,∠C=90°,AB垂直平分线交直线BC于D ,若
 ∠DAB=2∠DAC,则∠B的度数是(
)
∠DAB=2∠DAC,则∠B的度数是(
)
 A 18° B 36° C 54° D 30°
A 18° B 36° C 54° D 30°
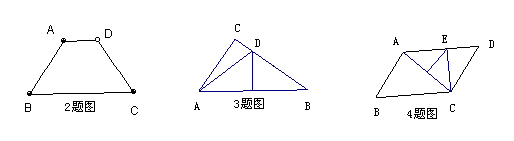
 4 如图,平行四边形ABCD中,AB=3,BC=5,AC的垂直平分线交
4 如图,平行四边形ABCD中,AB=3,BC=5,AC的垂直平分线交
 AD于E,则△CDE的周长为( )
AD于E,则△CDE的周长为( )

 A
6 B 8 C 9 D 10
A
6 B 8 C 9 D 10







 5在等边三角形ABC所在的平面内,存在着点P ,使△PAB、△PBC、△PAC都是等腰三角形,具有这样性质的点P共有(
)个
5在等边三角形ABC所在的平面内,存在着点P ,使△PAB、△PBC、△PAC都是等腰三角形,具有这样性质的点P共有(
)个
 A 1 个 B 6个 C
7个
D 10个
A 1 个 B 6个 C
7个
D 10个
 二填空题(每小题5分,共25分)
二填空题(每小题5分,共25分)
 6 三角形三边垂直平分线交于一点,这点到_____________________________的距离相等。
6 三角形三边垂直平分线交于一点,这点到_____________________________的距离相等。

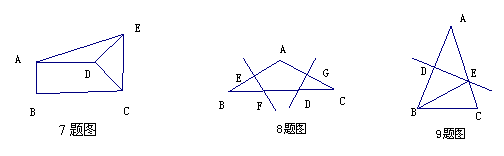 7(2007泰州)如图,直角梯形
7(2007泰州)如图,直角梯形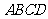 中,
中,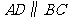 ,
,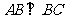 ,
,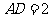 ,
,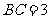 ,
,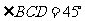 ,将腰
,将腰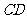 以点
以点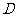 为中心逆时针旋转
为中心逆时针旋转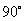 至
至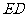 ,连结
,连结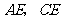 ,则
,则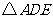 的面积是 .
的面积是 .








|
 9如图,△ABC中,AB=AC,DE是AB的垂直平分线,△BCE的周长为14,BC=6,则AB=_______.
9如图,△ABC中,AB=AC,DE是AB的垂直平分线,△BCE的周长为14,BC=6,则AB=_______.
 10 用反证法证明:“一个三角形中至少有一个内角大于或等于60°”时,应假设_____________________________________
10 用反证法证明:“一个三角形中至少有一个内角大于或等于60°”时,应假设_____________________________________
 三 解答题(每小题10分,共50分)
三 解答题(每小题10分,共50分)
 11 党和政府十分关心四川灾后重建工作,准备为三个村庄A、B、C(其位置如图所示)修建一口水井,要求水井到三个村庄的距离相等,水井应该修在什么地方呢,你能找到吗?
11 党和政府十分关心四川灾后重建工作,准备为三个村庄A、B、C(其位置如图所示)修建一口水井,要求水井到三个村庄的距离相等,水井应该修在什么地方呢,你能找到吗?

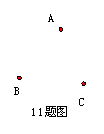 (写出作法,并保留作图痕迹)
(写出作法,并保留作图痕迹)








 12 已知:等腰三角形ABCD,AD∥BC,对角线AC⊥BD,相交于点O ,AD=3cm,BC=7cm,求梯形的面积S
12 已知:等腰三角形ABCD,AD∥BC,对角线AC⊥BD,相交于点O ,AD=3cm,BC=7cm,求梯形的面积S







 13(2007嘉兴)如图,等腰梯形ABCD中,AD∥BC,点E是AD延长线上一点,DE=BC.
13(2007嘉兴)如图,等腰梯形ABCD中,AD∥BC,点E是AD延长线上一点,DE=BC.

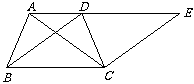 (1)求证:∠E=∠DBC;
(1)求证:∠E=∠DBC;
 (2)判断△ACE的形状(不需要说明理由).
(2)判断△ACE的形状(不需要说明理由).

|







 14 用反证法证明:一条线段只有一个中点
14 用反证法证明:一条线段只有一个中点





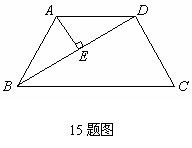
 15(2007北京)如图,在梯形ABCD中,AD∥BC,AB=DC=AD,∠C=60°,AE⊥BD于点E,AE=1,求梯形ABCD的高。
15(2007北京)如图,在梯形ABCD中,AD∥BC,AB=DC=AD,∠C=60°,AE⊥BD于点E,AE=1,求梯形ABCD的高。










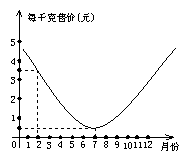
13.某农场种植一种蔬菜,销售员根据往年的销售情况,对今年这种蔬菜的销售价格进行了预测,预测情况如图,图中的抛物线(部分)表示这种蔬菜销售价与月份之间的关系,观察图象,你能得到关于这种蔬菜的哪些信息?
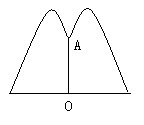
12.如图所示,公园要造圆形的喷水池, 在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面距离最大,高度2.25m.
若不计其他因素, 那么水池的半径至少要多少米才能使喷出的水流不致落到池外?
11.抛物线y=x2-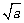 x+a2的顶点在直线y=2上,求a的值.
x+a2的顶点在直线y=2上,求a的值.
10.当一枚火箭被竖直向上发射时,它的高度h(m)与时间t(s)的关系可以用
h= -5t2+150t+10表示,经过多长时间,火箭到达它的最高点?最高点的高度是多少?
9.函数y=(x+1)(x-2)的图象的对称轴是______,顶点为________.
8.如图所示,已知抛物线y=ax2+bx+c的图象, 试确定下列各
式的符号:
a____0,b____0,c_____0;a+b+c_____0,a-b+c_____0.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com