
题目列表(包括答案和解析)
8.在半径为4cm 的圆中, 挖去一个半径为xcm 的圆面, 剩下一个圆环的面积为ycm2,则y与x的函数关系式为( )
A.y=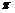 x2-4 B.y=
x2-4 B.y=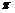 (2-x)2; C.y=-(x2+4) D.y=-
(2-x)2; C.y=-(x2+4) D.y=-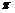 x2+16
x2+16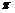
7.下列函数中,不是二次函数的是( )
A.y=1-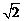 x2 B.y=2(x-1)2+4; C.y=
x2 B.y=2(x-1)2+4; C.y=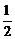 (x-1)(x+4)
D.y=(x-2)2-x2
(x-1)(x+4)
D.y=(x-2)2-x2
6.下列结论正确的是( )
A.二次函数中两个变量的值是非零实数; B.二次函数中变量x的值是所有实数;
C.形如y=ax2+bx+c的函数叫二次函数;
D.二次函数y=ax2+bx+c中a,b,c的值均不能为零
5.用一根长为8m的木条,做一个长方形的窗框,若宽为xm,则该窗户的面积y(m2)与x(m)之间的函数关系式为________.
4.在边长为4m的正方形中间挖去一个长为xm的小正方形, 剩下的四方框形的面积为y,则y与x间的函数关系式为_________.
3.填表:
|
c |
2 |
|
6 |
|
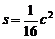 |
|
1 |
|
4 |
2.已知正方形的周长是ccm,面积为Scm2,则S与c之间的函数关系式为_____.
1.已知函数y=(k+2)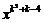 是关于x的二次函数,则k=________.
是关于x的二次函数,则k=________.
19、 (湘西自治州附加题,有改动)如图5,已知A(2,2),B(3,0).动点P(m,0)在线段OB上移动,过点P作直线l与x轴垂直.
(1)设△OAB中位于直线l左侧部分的面积为S,写出S与m之间的函数关系式;
(2)试问是否存在点P,使直线l平分△OAB的面积?若有,求出点P的坐标;若无,请说明理由.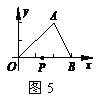

17.(本题10分)) 杭州休博会期间,嘉年华游乐场投资150万元引进一项大型游乐设施.若不计维修保养费用,预计开放后每月可创收33万元.而该游乐设施开放后,从第1个月到第x个月的维修保养费用累计为y(万元),且y=ax2+bx;若将创收扣除投资和维修保养费用称为游乐场的纯收益g(万元),g也是关于x的二次函数.
(1)若维修保养费用第1个月为2万元,第2个月为4万元.求y关于x的解析式;
(2)求纯收益g关于x的解析式;
(3)问设施开放几个月后,游乐场的纯收益达到最大?几个月后,能收回投资?
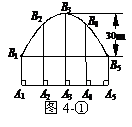
18(本题10分)如图所示,图4-①是一座抛物线型拱桥在建造过程中装模时的设计示意图,拱高为30m,支柱A3B3=50m,5根支柱A1B1、A2B2、A3B3、A4B4、A5B5之间的距离均为15m,B1B5∥A1A5,将抛物线放在图4-②所示的直角坐标系中.
(1)直接写出图4-②中点B1、B3、B5的坐标;
(2)求图4-②中抛物线的函数表达式;
(3)求图4-①中支柱A2B2、A4B4的长度.
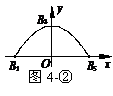
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com