2．在函数y=ax²+bx+c中，a,b,c分别是二次项系数、一次项系数及常数项．

课内同步精练

●A组　　 基础练习

1．形如y=ax²+bx+c(a,b,c是常数，a≠0)的函数，叫二次函数．

2.1二次函数

[知识要点]

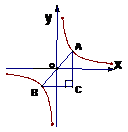
5. 如下图，点A.点B是y=的图像上关于原点对称的两点，且AC//y轴，BC//x轴，△ABC面积为S, 则　 S的值为(　 )

A　 S=1　 　B1<S<2　　　 C　 S= 2　　　 　DS>2

　　　　 5题　　　　　　　　　　　　 6题

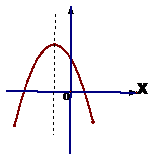
6 函数y=ax² +bx+c (a≠ 0)的图像如图所示，则下列结论正确的个数是(　　 )

(1)　 a+b+c<0　 (2)　 a-b+c>　 (3) abc>0　 　(4)　 2a-b=0

A　 1 　　　B　 2 　　　C　 3　 　　D　 4

7已知一次函数y=ax +b，与二次函数y=ax² +bx+c在同一坐标系里，他们的图像可能是(　　　 )

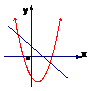
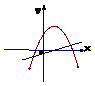
A　　　　　 B　　　　　　 C　　　　　　 D

8 如图在Rt △ABC中，∠C=90⁰ AC=4　 BC=8　 P是AB上一动点，直线PQ⊥AC于Q,设AQ=x,则△AQP面积y与x之间的函数图像大致为(　　 )

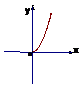
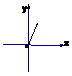
8题　　　 A　　　　 B　　　 C　　　　 D

二填空

1抛物线y=(x+2)²-5的开口方向­­­­­­­______，对称轴_____，顶点坐标_______。

2若抛物线y=mx^m-2m-1的开口向下，则m=______

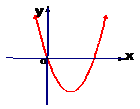
3如图是二次函数y=ax² –x+a²-1的图像。则a的值是____

4顶点为(-2 ，-5)且过(1，-4)的抛物线解析式为_________

5抛物线y=-x² –2x+m的顶点在x轴上，则m=_______

三解答题

1二次函数过A(-1,0) B(0,-3)两点，且对称轴是X=1求出它的解析式

2已知二次函数y=-x² –x+4回答下列问题

(1)　　　 用配方法将其化成y=a (x-h)²+k的形式

(2)　　　 指出抛物线的顶点坐标和对称轴

(3)　　　 当x取何值时，y随x增大而增大;

当x取何值时，y随x增大而减小？

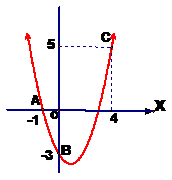
3已知如图，二次函数y=ax² +bx+c的图像过A、B、C三点

(1)　　　 观察图像写出A、B、C三点的坐标

(2)　　　 求出二次函数的解析式

4若直线y=x-2与抛物线y=ax² +bx+c相交于A(2,m)、B(n,3),抛物线对称轴为x=3, 求抛物线解析式

5通过研究发现：学生的注意力随老师讲课时间变化而变化。讲课开始时，学生的兴趣激增，中间一段时间，学生注意力保持较理想状态，随后学生的注意力开始分散。学生的注意力y随时间x(分钟)变化的图像如图所示，当0≤x≤10时图像是抛物线的一部分，当10≤ x ≤20　 20 ≤x ≤40时，图像都是线段。

(1)开始多少分钟时，学生的注意力最强？能保持多少时间？

(2)x 在什么范围内，学生的注意力随老师讲课时间增加而逐渐增强？x 在什么范围内，学生的注意力随老师讲课时间增加而逐渐降低？

(3)当20≤ x ≤40 时，求注意力y随与时间x(分钟)的函数关系式？

四解答题

1已知：o为坐标原点，∠ AOB=30⁰　 , ∠ABO=90⁰　 且A(2,0)

求　 过A、B、O三点的二次函数解析式

2如图一次函数图像与x 轴y轴交于A(6,0) B(0,2)线段AB的垂直平分线交x 轴于点C交y轴于点D

求 (1)求这个一次函数的解析式

(2)过A,B,C三点的抛物线解析式

五应用题

1如图，人工喷泉有一个竖直的喷水枪AB , 喷水口A距地面2米，喷水水流的轨迹是抛物线，如果要求水流的最高点P到喷水枪AB所在直线的距离为1米，且水流着地点C距离水枪底部B的距离为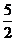米，那么水流的最高点距离地面是多少米？

2 用长为24米的篱笆，一面利用10米的墙，围成一个中间隔有一道篱笆的长方形花园。设花园的宽AB为x米，面积为y米²

(1)　　　 求y与x之间的函数关系式

(2)　　　 当宽AB为多少是，围成面积最大？

六解答题

1如下图，Rt △ABC的顶点A是双曲线y=与直线y=-x-(k+1)在第二象限的交点，AB⊥ x 轴于B，且 S_△ABC=

(1)　 求 这两个函数的解析式

(2)　 求直线与双曲线的两个交点A、C的坐标及△A OC的面积

2 如图，B，C，D三点是∠ MAN的边AM和AN上的三个动点，且∠BDC 和∠BCA保持相等，如果BC=3，AB=Y，BD=X写出Y和X之间的函数关系式

七解答题

某商人如果将进价为8元的商品按每件10元出售，每天可销售100件。现采用提高售出价，减少进货量的方法增加利润。已知这种商品每涨价1元其销售量就要减少10件，问他将售出价定为多少元时，才能使每天所赚的利润最大？并求出最大利润？

八解答题

如图，点A(4,m)在一次函数y=2x-4 和二次函数y=ax²的图像上，过点A作直线y=n的垂线，垂足为E, 点E关于直线y=2x-4 的对称点F在y轴上，点C是直线y=2x-4与y轴的交点。

(1)　　　 求二次函数解析式

(2)　　　 求实数n的值

(3)　　　 二次函数y=ax²的图像上是否存在一点P，且满足PA=PC，若存在，求出点P坐标；若不存在，说明理由？

8．已知抛物线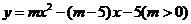与x轴交于两点、

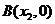
，与y轴交于点C，且AB=6．

(1)求抛物线和直线BC的解析式．

(2)在给定的直角坐标系中，画出抛物线和直线BC．

(3)若过A、B、C三点，求的半径．

(4)抛物线上是否存在点M，过点M作轴于点N，使被直线BC分成面积比为的两部分？若存在，请求出点M的坐标；若不存在，请说明理由．

7．已知抛物线y＝－x²+mx－m+2．　

(Ⅰ)若抛物线与x轴的两个交点A、B分别在原点的两侧，并且AB＝，试求m

　的值；

(Ⅱ)设C为抛物线与y轴的交点，若抛物线上存在关于原点对称的两点M、N，并且 △MNC的面积等于27，试求m的值．

6．如图，一单杠高2.2米，两立柱之间的距离为1.6米，将一根绳子的两端栓于立柱与铁杠结合处，绳子自然下垂呈抛物线状．

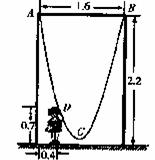
(1)　　　　　　　　 (2)

??(1)一身高0.7米的小孩站在离立柱0.4米处，其头部刚好触上绳子，求绳子最低点到地面的距离；

??(2)为供孩子们打秋千，把绳子剪断后，中间系一块长为0.4米的木板，除掉系木板用去的绳子后，两边的绳长正好各为2米，木板与地面平行．求这时木板到地面的距离(供选用数据：≈1.8，≈1.9，≈2.1)

5．某工厂设门市部专卖某产品，该产品每件成本40元，从开业一段时间的每天销售统计中，随机抽取一部分情况如下表所示：

假设当天定的售价是不变的，且每天销售情况均服从这种规律．

(1)观察这些统计数据，找出每天售出件数与每件售价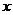(元)之间的函数关系，并写出该函数关系式．

(2)门市部原设有两名营业员，但当销售量较大时，在每天售出量超过168件时，则必须增派一名营业员才能保证营业有序进行，设营业员每人每天工资为40元．

求每件产品应定价多少元，才能使每天门市部纯利润最大(纯利润指的是收入总价款扣除成本及营业员工资后的余额，其它开支不计)

4．已知函数y=x²+bx-1的图象经过点(3，2)

(1)　　　 求这个函数的解析式；

(2)　　　 画出它的图象，并指出图象的顶点坐标；

(3)　　　 当x>0时，求使y≥2的x的取值范围．

3．看图，解答下列问题．

　(1)求经过A、B、C三点的抛物线解析式；

　(2)通过配方，求该抛物线的顶点坐标和对称轴；

　(3)用平滑曲线连结各点，画出该函数图象．