42.如图13-3-20，已知抛物线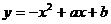与x轴从左至右交于A，B两点，

与y轴交于点C，且∠BAC=α，∠ABC=β，tgα-tgβ=2,∠ACB=90°.

(1)　　　　　　　 求点C的坐标；

(2)　　　　　　　 求抛物线的解析式；

(3)　　　　　　　 若抛物线的顶点为P，求四边形ABPC的面积.

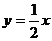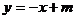41.已知直线和，二次函数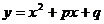图象的顶点为M.

(1)　　　　　　　 若M恰在直线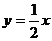与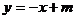的交点处，试证明：无论m取何实数值，

二次函数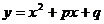的图象与直线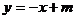总有两个不同的交点.

(2)　　　　　　　 在(1)的条件下，若直线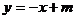过点D(0，-3)，求二次函数

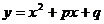的表达式，并作出其大致图象.

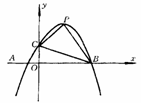
图13-3-20

(3)　　　　　　　 在(2)的条件下，若二次函数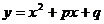的图象与y轴交于点C，与x同

的左交点为A，试在直线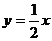上求异于M点P，使P在△CMA的外接圆上.

40.如图13-3-19，在直角坐标系中，以AB为直径的⊙C交x轴于A，交y轴于B，

满足OA∶OB=4∶3，以OC为直径作⊙D，设⊙D的半径为2.

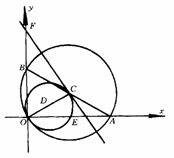
图13-3-19

(1)　 求⊙C的圆心坐标.

(2)　 过C作⊙D的切线EF交x轴于E，交y轴于F，求直线EF的解析式.

(3)　 抛物线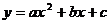(a≠0)的对称轴过C点，顶点在⊙C上，与y轴交点为B，求抛物线的解析式.

39.已知二次函数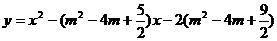的图象与x轴的交点为

A，B(点A在点B右边)，与y轴的交点为C.

(1)　 若△ABC为Rt△，求m的值；

(2)　 在△ABC中，若AC=BC，求∠ACB的正弦值；

(3)　 设△ABC的面积为S，求当m为何值时，S有最小值，并求这个最小值.

38.已知：如图13-3-18，EB是⊙O的直径，且EB=6，在BE的延长线上取点P，使EP=EB.A

是EP上一点，过A作⊙O的切线AD，切点为D，过D作DF⊥AB于F，过B作AD的垂线BH，交AD的延长线于H，连结ED和FH.

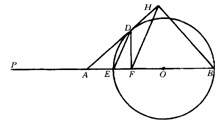
图13-3-18

(1)　 若AE=2，求AD的长.

(2)　 当点A在EP上移动(点A不与点E重合)时，①是否总有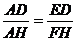？试证 明 你的结论；②设ED=x，BH=y，求y与x的函数关系式，并写出自变量x的取值范围.

37.如果抛物线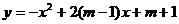与x轴都交于A，B两点，且A点在x轴

的正半轴上，B点在x同的负半轴上，OA的长是a，OB的长是b.

(1)　　　　 求m的取值范围；

(2)　　　　 若a∶b=3∶1，求m的值，并写出此时抛物线的解析式；

(3)　　　　 设(2)中的抛物线与y轴交于点C，抛物线的顶点是M，问：抛物线上是否存 在　 点P，使△PAB的面积等于△BCM面积的8倍？若存在，求出P点的坐标；若不存在，请 说明理由.

36.已知：抛物线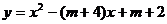与x轴交于两点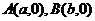(a<b).O

为坐标原点，分别以OA，OB为直径作⊙O₁和⊙O₂在y轴的哪一侧？简要说明理由，并指出两圆的位置关系.

35.如图13-3-17，这是某市一处十字路口立交桥的横断面在平面直角坐标系中的示

意图，横断面的地平线为x轴，横断面的对称轴为y轴，桥拱的DGD＇部分为一段抛物线，顶点C的高度为8米，AD和A＇D＇是两侧高为5.5米的支柱，OA和OA＇为两个方向的汽车通行区，宽都为15米，线段CD和C＇D＇为两段对称的上桥斜坡，其坡度为1∶4.

求(1)桥拱DGD＇所在抛物线的解析式及CC＇的长；

(2)BE和B＇E＇为支撑斜坡的立柱，其高都为4米，相应的AB和A＇B＇为两个方

向的行人及非机动车通行区，试求AB和A＇B＇的宽；

(3)按规定，汽车通过该桥下时，载货最高处和桥拱之间的距离不得小于0.4米，车

载大型设备的顶部与地面的距离均为7米，它能否从OA(或OA＇)区域安全通过？请说明理由.

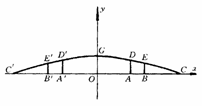
图13-3-17

34.中图13-3-16，抛物线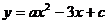交x轴正方向于A，B两点，交y轴正方

向于C点，过A，B，C三点做⊙D，若⊙D与y轴相切.(1)求a，c满足的关系；(2)设∠ACB=α，求tgα；(3)设抛物线顶点为P，判断直线PA与⊙O的位置关系并证明.

33.如图13-3-15，抛物线与直线y=k(x-4)都经过坐标轴的正半轴上A，B两点，该

抛物线的对称轴x=-21与x轴相交于点C，且∠ABC=90°，求：(1)直线AB的解析式；(2)抛物线的解析式.

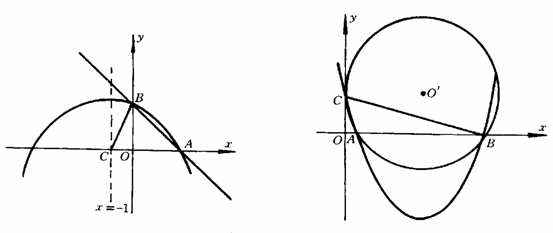
　　 　　　 图13-3-15　　　　　　　　　　　　　 　　　　 图13-3-16