
题目列表(包括答案和解析)
例2(厦门)一定质量的干松木,当它的体积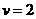 m3时,它的密度
m3时,它的密度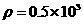 kg/m3,则
kg/m3,则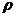 与
与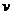 的函数关系式是( )
的函数关系式是( )
A.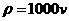 B.
B.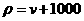 C.
C.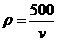 D.
D.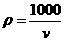
解:由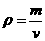 ,当
,当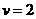 m3时,它的密度
m3时,它的密度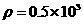 kg/m3时,有
kg/m3时,有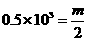 ,解得:
,解得: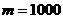 ,所以,
,所以,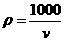 ,故选D.
,故选D.
例1(海南)在匀速运动中,路程 一定时,速度
一定时,速度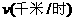 关于时间
关于时间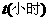 的函数关系的大致图象是( )
的函数关系的大致图象是( )
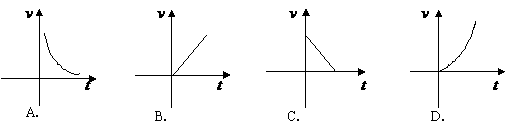
解:由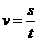 ,当路程
,当路程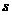 一定时,速度
一定时,速度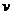 是关于时间
是关于时间 的反比例函数,所以它的图象是双曲线,又
的反比例函数,所以它的图象是双曲线,又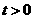 ,所以图象在第一象限,故选A.
,所以图象在第一象限,故选A.
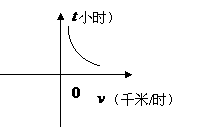
例3 甲、乙两地相距100千米,一辆汽车从甲地开往乙地,把汽车到达乙地所用的时间 (小时)表示为汽车速度
(小时)表示为汽车速度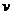 (千米/时)的函数,并画出函数的图象.
(千米/时)的函数,并画出函数的图象.
错解:由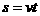 ,得
,得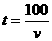 .用描点法画出函数
.用描点法画出函数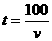 的图象.
的图象.
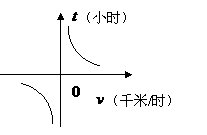

错解分析:错解中忽略了自变量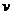 的取值范围
的取值范围 ,而误认为
,而误认为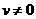 .
.
正确解法:由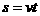 ,得
,得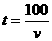 .用描点法画出函数
.用描点法画出函数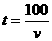 的图象.
的图象.

物理中的反比例函数
九年义务教育初中数学教学要求中指出“解决实际问题主要是能够解决带有实际意义的和相关学科中的数学问题,以及解决生产和日常生活中的实际问题”.近年来,各地的中考题充分体现了这个教学要求,在试题中涉及了物理、化学等学科的知识,对综合应用能力越来越突出.下面以反比例函数在物理中各个方面的应用为例加以说明.
例2 在函数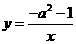 (
(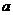 为常数)的图象上有三点
为常数)的图象上有三点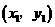 ,
,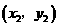 ,
,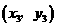 ,且
,且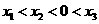 ,则函数
,则函数 的大小关系是( )
的大小关系是( )
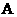 .
.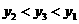
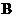 .
.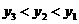
 .
.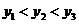
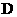 .
.
错解: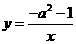 是反比例函数,且
是反比例函数,且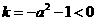 ,∴
,∴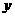 随
随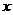 的增大而增大∵
的增大而增大∵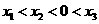 ,∴
,∴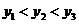 ,故选
,故选 .
.
错解分析:当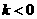 时,反比例函数的图象在第二、四象限内,且在每一象限内,
时,反比例函数的图象在第二、四象限内,且在每一象限内,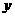 随
随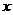 的增大而增大,而点
的增大而增大,而点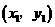 ,
,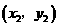 ,
,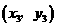 不在同一象限内,因而不能由
不在同一象限内,因而不能由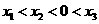 得到
得到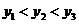 .
.
正确解法:∵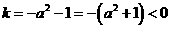 ,∴
,∴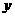 随
随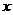 的增大而增大,且函数图象分布在二、四象限内,
的增大而增大,且函数图象分布在二、四象限内,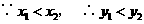 . ∵
. ∵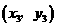 在第四象限,而
在第四象限,而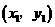 和
和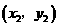 在第二象限,∴
在第二象限,∴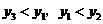 ,∴
,∴ .故选
.故选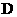 .
.
例1 当 为 时,函数
为 时,函数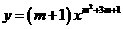 是反比例函数.
是反比例函数.
错解:根据反比例函数的定义,得 ,即
,即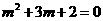 .解得
.解得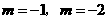 .
.
错解分析:错解忽略了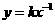 中的
中的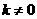 是反比例函数定义的重要组成部分.本题的
是反比例函数定义的重要组成部分.本题的 不仅满足
不仅满足 而且更要满足
而且更要满足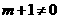 .
.
正确解法:根据题意,得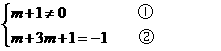
由①得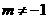 ,由②得
,由②得 ,∴
,∴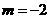 .
.
3.如何用坐标表示线段的长?
[思路分析] 在坐标平面上怎样求三角形的面积?
解:应用对称点坐标的特点分别找A,B,C各点坐标.
设(x0,y0),则B(-x0,-y0).
∵AC∥y轴,BC∥x轴,
∴C(x0,-y0).
∴S△ABC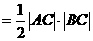
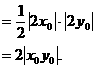
∵点A(x0,y0)在函数 的图象上.
的图象上.
∴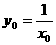 ,即x0y0=1.
,即x0y0=1.
∴S△ABC=2,即S=2.
∴应选C.
[扩散2]
如图,Rt△AOB的顶点A在双曲线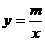 ,且S△AOB=3,求m的值.
,且S△AOB=3,求m的值.

[思路分析] 给定条件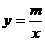 说明什么?如何利用S△AOB=3这一条件?
说明什么?如何利用S△AOB=3这一条件?
设A(x,y),则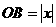 ,
,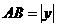 ,求m,即求x·y.
,求m,即求x·y.
则由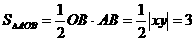 ,求得:
,求得: .
.
∵点A(x,y)在双曲线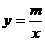 上,
上,
∵m>0,∴m=6.
[扩散3]
反比例函数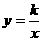 (k>0)在第一象限内的图象如图所示,P为该图象上任一点,PQ⊥x轴,设△POQ的面积为S,则S与k之间的关系是( ).
(k>0)在第一象限内的图象如图所示,P为该图象上任一点,PQ⊥x轴,设△POQ的面积为S,则S与k之间的关系是( ).

A.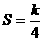 B.
B.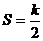 C.S=k
D.S>k
C.S=k
D.S>k
与扩散2思路相仿,请读者完成(答案B).
[扩散4] 已知点P1(x1,y1)和P2(x2,y2)都在反比例函数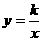 (k<0)的图象上,试比较矩形P1AOB和矩形P2COD的面积大小.
(k<0)的图象上,试比较矩形P1AOB和矩形P2COD的面积大小.
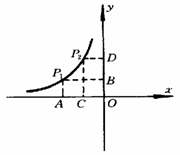
[思路分析] 在坐标平面上怎样求矩形的面积?
应用坐标的特点找到矩形各顶点坐标,再利用矩形面积公式,求得面积值进行比较.
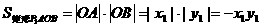 ,
,
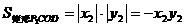 .
.
∵点P1(x1,y1),P2(x2,y2)都在反比例函数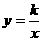 (k<0,x<0)的图象上.
(k<0,x<0)的图象上.
∴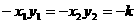 >0(k<0),即
>0(k<0),即 .
.
[扩散5]
已知函数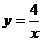 的图象和两条直线y=x,y=2x在第一象限内分别相交于P1
的图象和两条直线y=x,y=2x在第一象限内分别相交于P1
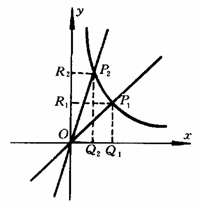 和P2两点,过P1分别作x轴、y轴的垂线P1Q1,P1R1,垂足分别为Q1,R1,过P2分别作x轴、y轴的垂线P2Q2,P2R2,垂足分别为Q2,R2,求矩形OQ1P1R1和OQ2P2R2的周长,并比较它们的大小.
和P2两点,过P1分别作x轴、y轴的垂线P1Q1,P1R1,垂足分别为Q1,R1,过P2分别作x轴、y轴的垂线P2Q2,P2R2,垂足分别为Q2,R2,求矩形OQ1P1R1和OQ2P2R2的周长,并比较它们的大小.
[思路分析] 解本例的关键是什么,求矩形周长应先确定哪几个点的坐标?
本例的关键是求出P1,P2的坐标,要求P1,P2两点坐标就要利用y=x,y=2x和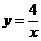 .
.
设P1(x1,y1),P2(x2,y2).
∵P1,P2分别为y=x,y=2x与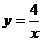 在第一象限内的交点,
在第一象限内的交点,
∴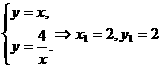 .
.
∴矩形OQ1P1R1的周长=2(2+2)=8.
同理: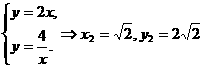 .
.
∴矩形OQ2P2R2的周长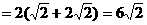 .
.
则 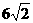 >6×1.4>8.
>6×1.4>8.
即矩形OQ2P2R2的周长大于矩形OQ1P1R1的周长.
[扩散6]
如图,面积为3的矩形OABC的一个顶点B在反比例函数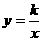 的图象上,
的图象上,
另3个点在坐标轴上,则k= .
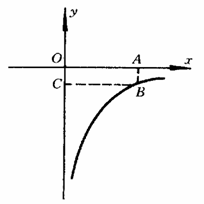
[思路分析] 解本例的关键是什么?怎样求B点坐标?
从图象和已知条件可知解本例关键是求出B点坐标.求B点坐标要利用矩形面积等于3这一条件.
设B(x,y),则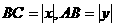 .
.
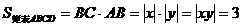 .
.
∵点B在反比例函数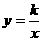 的图象上,
的图象上,
∴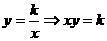 (k<0).
(k<0).
∴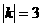 (k<0).
(k<0).
∴k=-3.
小结:从扩散1-6可知,对称点坐标的特点,点与图象之间一一对应关系,是解决问
题的关键,无论求面积或用面积求系数k,变化求周长等,都利用了这些基础知识,抓住它,再结合面积公式、周长公式等,问题迎刃而解.本例命题改变的思维扩散,目的就是灵活运用基础知识去解决问题.
错例剖析
有m部同样的机器一齐工作,需要m小时完成一项任务.
(1)设由x部机器(x为不大于m的正整数)完成同一任务,求所需时间y(小时)
与机器的总数x的函数关系式.
(2)画出所求函数当m=4时的图象.
解:(1)一部机器一小时能完成这项任务的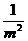 ,则x部机器一个小时能完成这项任务的
,则x部机器一个小时能完成这项任务的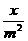 ,x部机器完成这项任务所需时间(小时)
,x部机器完成这项任务所需时间(小时)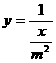 ,即
,即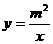 (x为不大于m的正整数).
(x为不大于m的正整数).
(2)当m=4时,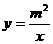 即
即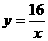 (x为不大于4的正整数).
(x为不大于4的正整数).
|
X |
… |
1 |
2 |
3 |
4 |
… |
|
y |
… |
16 |
8 |
5.3 |
4 |
… |
|
|
|
|
|
|
|
|

错因剖析
本例在求解过程中,思路清晰、准确地求出解析式,并严格按照画图象的步骤进行(列
表、描点、连线).由于知识学得死,又不能考虑实际情况,因此在画图象时三次出现错误:
(1)列表不能用省略号.因x是小于等于4的正整数.(2)不能用平滑的曲线连线.因
为机器必须是完整的,即用正整数表示,所以图象是正整数点.(3)图象向两方无限延伸也是错误的,即使能延伸,只是点延伸,也不能曲线延伸,何况自变量x是不大于4的正整数,根本不能延伸.可见,在学好书本知识,把它应用于具体实践中时,必须打破原来的思维定势的桎梏(列表用省略号,描点连线,向两方无限延伸),“列表、描点、连线”那是最基础的,一定要熟练掌握,但在具体应用所学知识时,千万要打破“框框”,要根据具体情况,决定策略,否则会出现各种各样错误.本例再次提醒我们,只有理论联系实际,才能学到真正知识.
原解答在列表、画图、连线时出现三处错误,其他均正确,现纠错如下:
|
x |
1 |
2 |
3 |
4 |
|||
|
|
16 |
8 |
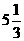 |
4 |
2.(1)下列函数中,反比例函数是 .
A.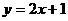 B.
B.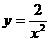 C.
C.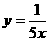 D.
D.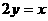
(2)已知:(x1,y1)和(x2,y2)是双曲线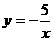 上两点,当x1<x2<0时,y1与y2
上两点,当x1<x2<0时,y1与y2
的大小关系是 .
A.y1=y2 B.y1<y2 C.y1>y2 D.y1与y2的大小关系不确定
(3)若函数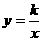 的图象过点(3,-7),那么它一定还经过点
.
的图象过点(3,-7),那么它一定还经过点
.
A.(3,7) B.(-3,-7) C.(-3,7) D.(2,-7)
(4)若反比例函数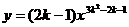 的图象位于第二、四象限,则k的值是 .
的图象位于第二、四象限,则k的值是 .
A.0 B.0或1 C.0或2 D.4
学法指要
[例] 如图,在等腰梯形ABCD中,CD∥AB,CD=6,AD=10,∠A=60°,以
CD为弦的弓形弧与AD相切于D,P是AB上一动点,可以与B重合但不与A重合,DP交弓形弧于Q.
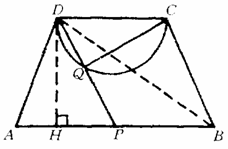
(1)求证:△CDQ∽△DPA;
(2)设DP=x,CQ=y,试写出y关于自变量x的解析式,并求出x的取值范围;
(3)当DP之长是方程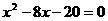 的一根时,求四边形PBCQ的面积.
的一根时,求四边形PBCQ的面积.
[思路分析] 根据题设找两个三角形相似的条件,第一问迎刃而解,要求y与x之
间关系,当然要借助几何知识建立关系,观察图形可知,y和x与三角形相似息息相关,三角形相似已证,由此又使思路沟通.第三问首先解一元二次方程,求出DP,进一步可求出四边形PBCQ的面积.
[思考](1)判定两个三角形相似的条件是什么?本例中有没有这样的条件?
解:由梯形的性质,DC∥AB,可知∠CDQ=∠DPA.由弦切角的性质可知,∠DCQ=∠PDA;故△CDQ∽△DPA.
[思考](2)函数关系怎么建立?首先从图上看DP=x与CQ=y有什么关系?给定的已知条件与DP,CQ有什么关系?
解:从图形中不难分析出CQ,DP,DA,CD可转化为两相似三角形的对应边.
即CQ∶DA=CD∶DP,y∶10=6∶x,
∴
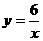 .
.
这里要求的是DP=x的取值范围,DP的长短决定于什么?P点在什么范围运动?观察P
点的运动过程,P点到什么位置时,DP最长?P点运动到什么位置时,DP最短?
∵动点P可与B重合,也可与D在AB上的射影H重合,且D与线段AB上的点的连线中,以DB最长,DH最短.
∴DH≤DP≤DB,即DH≤x≤DB.
∵在 Rt△AHD中,可得
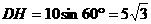 ,∴
,∴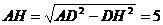 .
.
∴
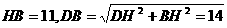 .
.
∴
5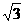 ≤x≤14.
≤x≤14.
[思考] (3)四边形PBCQ在图形中占有什么位置?给定的一元二次方程与求四边
形PBCQ的面积有什么关系?
解:用图形分割法,从图上不难看出,四边形PBCQ=梯形ABCD-△DPA-△CDQ.
现在看梯形ABCD的面积、△DPA的面积、△CDQ的面积能否求.
S△DPA=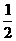 AP·DH.
AP·DH.
由给定的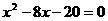 中,求得DP=10.
中,求得DP=10.
又AD=10,∠A=60°,∴△DPA是等边三角形.
即
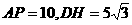 .
.
∴
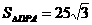 .
.
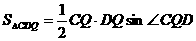 ,
,
由条件可知,△DCQ是等边三角形,DC=DQ=CQ=6,∠DQC=60°,
∴
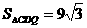 .
.
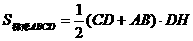 ,
,
由已知条件可知,DC=6,AB=AP+PB=10+6=16,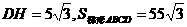 .
.
这就不难求出 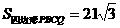 .
.
小结:从全题分析,由动到静,P点的移动是关键.研究动点要用静态去分析,本例第
3问的关键是由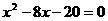 把P点定下来,才能有△ADP是等边三角形
把P点定下来,才能有△ADP是等边三角形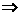 △DCQ是等边三角形
△DCQ是等边三角形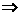 四边形PBCD是平行四边形.
四边形PBCD是平行四边形.
反比例函数与相似三角形、四边形、圆相结合为一体,又与一元二次方程水乳交融,这就给反比例蒙上神秘的色彩,给求反比例函数关系式设置了不少障碍.遇到这样复杂的问题时,一要认真剖析,把复杂化为简单;二要发挥数形结合的威力;三要集中“兵力”(即用所学基础知识,联想,类比,找到突破口),各个击破,这样便可把难题攻破,走出低谷.
思维体操
[扩散1]
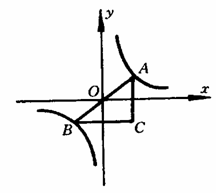 [例] 如图,A,B是函数
[例] 如图,A,B是函数 的图象上关于原点O对称的任意两点,AC∥y轴,BC∥x轴,△ABC的面积S,则
.
的图象上关于原点O对称的任意两点,AC∥y轴,BC∥x轴,△ABC的面积S,则
.
A.S=1 B.1<S<2 C.S=2 D.S>2
[思考] 1.关于x轴、y轴、原点对称的坐标有
何特点?2.平行于x轴、y轴坐标有什么特点?
1.(1)函数 叫做反比例函数;它的图象是 .
(2)反比例函数的性质:①当k>0,图象的两个分支分别在 象限,在每一
个象限内y随x的增大而 ,②k<0,图象的两个分支分别在 象限,在每一个象限内,y随x的增大而 .
(3)k为何值时,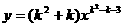 是反比例函数,即k=
.
是反比例函数,即k=
.
(4)反比例函数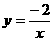 图象在
象限.
图象在
象限.
13.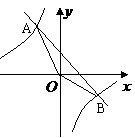 已知如图4,反比例函数
已知如图4,反比例函数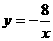 与一次函数
与一次函数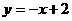 的图像交与A,B两点,求(1)A,B两点的坐标. (2)△AOB的面积.
的图像交与A,B两点,求(1)A,B两点的坐标. (2)△AOB的面积.
12.已知一次函数与反比例函数的图像都经过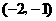 和
和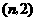 两点.求这两个函数的关系式.
两点.求这两个函数的关系式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com