4、下面图表的统计资料是衢州市统计局公布的2006年末衢州市辖区范围的6个县(市、区)人口分布的部分信息。

2006年衢州市各县(市、区)人口分布统计表

县(市、区)	柯城区	衢江区	龙游县	江山市	常山县	开化县
总人口(人)	410377	397675	402227	583312		346452

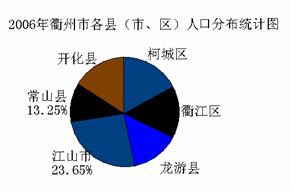(1)由图表可知，2006年末衢州市的总人口是___________人，常山县的总人口是________人(按四舍五入精确到个位)。

(2)柯城区的总人口数占衢州市总人口数的百分比是__________(精确到0.01%)。在扇形统计图中，表示柯城区的扇形的圆心角等于________度(精确到度)。

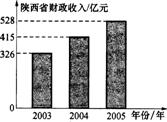
3、2003-2005年陕西省财政收入情况如图所示，根据图中的信息，解答下列问题：

(1)陕西省这三年财政收入共为多少亿元？

(2)陕西省2004-2005年财政收入的年增长率约为多少？(精确到1%)

(3)如果陕西省2005-2006年财政收入的年增长率与(2)中求得的年增长率基本相同.请估计陕西省2006年财政收入约为多少亿元？(精确到1亿元)

2、某网站公布了某城市一项针对2006年第一季度购房消费需求的随机抽样调查结果，下面是根据调查结果制作的购房群体可接受价位情况的比例条形统计图和扇形统计图的一部分．

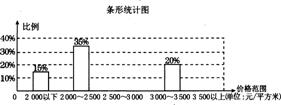
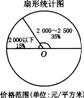
请根据统计图中提供的信息回答下列问题：

(1)若2500-3000可接受价位所占比例是3500以上可接受价位所占比例的5倍，则这两个可接受价位所占的百分比分别为　　　．

(2)补全条形统计图和扇形统计图；

(3)购房群体中所占比例最大的人群可接受的价位是　　　；

(4)如果2006年第一季度该市所有的有购房需求的人数为50000人，试估计这些有购房需求的人中可接受3500元／平方米以上的人数是　　　人．

1、如图是某班全体学生外出时乘车、步行、骑车的人数分布条形统计图和扇形统计图图(两图都不完整)，则下列结论中错误的是(　 )。

A、该班总人数为50人　　 B、骑车人数占总人数的20%

C、步行人数为30人　　 D、乘车人数是骑车人数的2.5倍

例1.某校九(1)班的全体同学最喜欢的球类运动用图所示的统计图来表示，下面说法正确的是(　　 )

A．从图中可以直接看出喜欢各种球类的具体人数；

B．从图中可以直接看出全班的总人数；

C．从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况；

D．从图中可以直接看出全班同学现在最喜欢各种球类的人数的大小关系。

例2.下面是两户居民家庭全年各项支出的统计图.

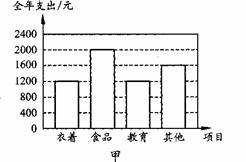
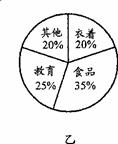
根据统计图，下列对两户教育支出占全年总支出的百分比作出的判断中，正确的是(　 )

A．甲户比乙户大 　　　　　　　B.乙户比甲户大

C．甲、乙两户一样大　 　　　　D.无法确定哪一户大

例3.光明中学七年级1班同学积极响应“阳光体育工程”的号召，利用课外活动时间积极参加体育锻炼，每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练，训练前后都进行了测试．现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表．

项目选择情况统计图　　　　　　　 训练后篮球定时定点投篮测试进球数统计表

请你根据图表中的信息回答下列问题：

(1)选择长跑训练的人数占全班人数的百分比是　　　　 ，该班共有同学　　　 人；

(2)求训练后篮球定时定点投篮人均进球数；

(3)根据测试资料，训练后篮球定时定点投篮的人均进球数比训练之前人均进球数增加25%．请求出参加训练之前的人均进球数．

例4.在暑期社会实践活动中，小明所在小组的同学与一 家玩具生产厂家联系，给该厂组装玩具，该厂同意他们组装240套玩具.这些玩具分为A、B、C三种型号，它们的数量比例以及每人每小时组装各种型号玩具的数量如图所示：

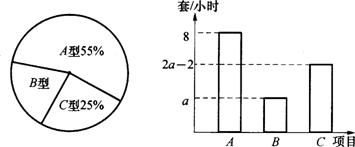若每人组装同一种型号玩具的速度都相同，根据以上信息，完成下列填空：

(1)从上述统计图可知，A 型玩具有　　　 套，B型玩具有　　　 套，C型玩具有　　 套.

(2)若每人组装A型玩具16套与组装C型玩具12套所花的时间相同，那么a的值为　　 ，每人每小时能组装C型玩具　　　　　 套.

例5(2006浙江金华)某年级组织学生参加夏令营活动,本次夏令营分为甲、乙、丙三组进行活动. 下面两幅统计图反映了学生报名参加夏令营的情况，请你根据图中的信息回答下列问题:

　　 报名人数条形统计图　　　　　　　　　 报名人数扇形分布图

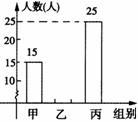
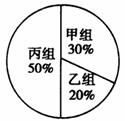
(1)该年级报名参加丙组的人数为　　　 ;

(2)该年级报名参加本次活动的总人数　　　 ，

(3)根据实际情况,需从甲组抽调部分同学到丙组,使丙组人数是甲组人数的3倍,应从甲组抽调多少名学生到丙组？

20、(2009年达州)如图8，直线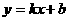与反比例函数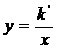(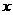＜0)的图象相交于点A、点B，与x轴交于点C，其中点A的坐标为(－2，4)，点B的横坐标为－4.

(1)试确定反比例函数的关系式；

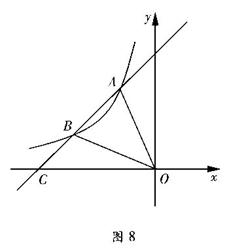(2)求△AOC的面积.

19、(2009河池)为了预防流感，某学校在休息天用药熏消毒法对教室进行消毒．已知药物释放过程中，室内每立方米空气中的含药量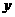(毫克)与时间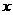(分钟)成正比例；药物释放完毕后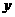，与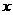成反比例，如图9所示．根据图中提供的信息，解答下列问题：

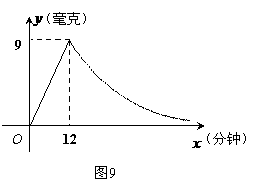(1)写出从药物释放开始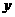，与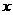之间的两个函数

关系式及相应的自变量取值范围；

(2)据测定，当空气中每立方米的含药量降低到0.45毫克

以下时，学生方可进入教室，那么从药物释放开始，

至少需要经过多少小时后，学生才能进入教室？

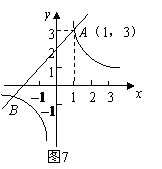
18、(2009肇庆)如图 7，已知一次函数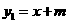(m为常数)的图象与反比例函数 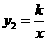(k为常数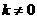， )的图象相交于点 A(1，3)．

(1)求这两个函数的解析式及其图象的另一交点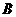的坐标；

(2)观察图象，写出使函数值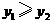的自变量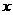的取值范围．

17．(本题8分)如图，第一象限的角平分线OM与反比例函数的图象相交于点A，已知OA=2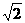.(1)求点A的坐标；(2)求此反比例函数的解析式.

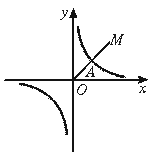
16．正比例函数y=x与反比例函数y=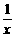的图象相交于A、C两点.AB⊥x轴于B,CD⊥y轴于D(如图),则四边形ABCD的面积为_______________