
题目列表(包括答案和解析)
3.某商场以80元/件的价格购进西服1000件,已知每件售价为100元时,可全部售出.如果定价每提高1%,则销售量就下降0.5%,问如何定价可使获利最大?(总利润=总收入-总成本).
2.某旅社有客房120间,每间房的日租金为50元时,每天都客满,旅社装修后要提高租金,经市场调查发现,如果每间客房的日租金每增加5元时,则客房每天出租数会减少6间,不考虑其他因素,旅社将每间客房的日租金提高到多少元时,客房日租金的总收入最高?
1.某商店购进一批单价为16元的日用品,销售一段时间后,为了获取更多利润, 商店决定提高销售价格,经试验发现,若按每件20元的价格销售时,每月能卖360件; 若按每件25元的价格销售时,每月能卖210件.假定每月销售件数y(件)是价格x( 元/件)的一次函数.
(1)试求y与x之间的函数关系式;
(2)在商品不积压,且不考虑其他因素的条件下,问销售价格为多少时,才能使每月获得最大利润?每月的最大利润是多少?(总利润=总收入-总成本).
2.6 何时获得最大利润 同步练习
1.2 一元二次方程的算法(3)公式法 同步练习
考标要求:1会用求根公式解一元二次方程;
2 会利用一元二次方程的判别式判断一元二次方程根的情况;
3 会选择适当的方法解一元二次方程;
重点:求根公式的推导过程,和用求根公式解一元二次方程;
难点:求根公式的推导过程和选择合适的方法解一元二次方程。
一 选择题(每小题5分,共25分)
1一元二次方程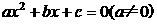 求根公式是( )
求根公式是( )
A 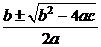 B
B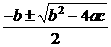
C
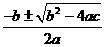 D
D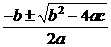 (
(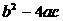 ≥0)
≥0)
2 方程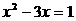 的判别式
的判别式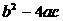 =( )
=( )
A 5 B 13 C -13 D -5
3关于x的方程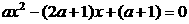 的根的情况下面说法正确的是( )
的根的情况下面说法正确的是( )
A 有两个不相等的实数根 B 没有实数根,C 有两个相等的实数根 D 当a=0时,方程有一个实数根,当a≠0时,方程有两个不相等的实数根。
4 解一元二次方程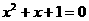 最合适的方法是( )
最合适的方法是( )
A 直接开平方法 B 因式分解法 C 配方法 D 公式法
5若2x+1与x-2互为倒数,则实数x=( )
A 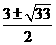 B
B 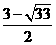 C
C 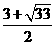 D
D 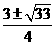
二 填空题(每小题5分,共25分)
6 已知y=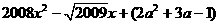 ,当x=0时,y=0,则a=_____;
,当x=0时,y=0,则a=_____;
7 x为_____时,分式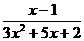 没有意义;
没有意义;
8 已知关于x的方程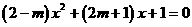 有两个相等的实数解,则m=______;
有两个相等的实数解,则m=______;
9 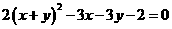 ,则x+y=_______
,则x+y=_______
10 点P在函数y=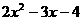 的图象上,且P的纵坐标为1 ,那么P点的横坐标为_____
的图象上,且P的纵坐标为1 ,那么P点的横坐标为_____
三 解答题(第11题20分,12题9分,13题5分,14、15各8分)
11 用公式法解下列方程
(1) 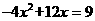 (2)(x-1)(2x+1)=2
(2)(x-1)(2x+1)=2
(3) 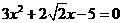 (4)
(4)
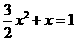
12 用适当的方法解下列方程
(1)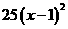 =36 (2)
=36 (2) 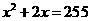 (3)
(3) 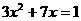
13 已知a、b、c是△ABC的三边长,且方程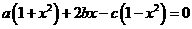 有相等的两个实数根,试判断△ABC的形状。
有相等的两个实数根,试判断△ABC的形状。
14 一个人拿一根竹竿前行,横放比门长3m,竖放比门高2m,沿门对角线斜放还长1m,那么这根竹竿有多长,门的宽和高分别为多少?
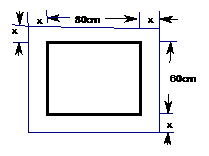 15在一副长为60cm,宽为80cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使挂图的面积为6300
15在一副长为60cm,宽为80cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使挂图的面积为6300 ,求金色纸边的宽。
,求金色纸边的宽。
2. 3 公理与定理 同步练习
3 公理与定理 同步练习
 考标要求:
考标要求:
 1 了解公理与定理到概念,以及他们之间的内在联系;
1 了解公理与定理到概念,以及他们之间的内在联系;
 2 了解公理与定理都是真命题,它们都是推理论证的依据;
2 了解公理与定理都是真命题,它们都是推理论证的依据;
 3 掌握教材十条公理和已学过的定理。
3 掌握教材十条公理和已学过的定理。
 重点难点
重点难点
 一 选择题(每小题5分,共25分)
一 选择题(每小题5分,共25分)
 1 下面命题中:
1 下面命题中:
 (1)旋转不改变图形的形状和大小, (2)轴反射不改变图形的形状和大小
(1)旋转不改变图形的形状和大小, (2)轴反射不改变图形的形状和大小
 (3)连接两点的所有线中,线段最短,(4)三角形的内角和等于180°
(3)连接两点的所有线中,线段最短,(4)三角形的内角和等于180°
 属于公理的有( )
属于公理的有( )
 A 1个 B 2个 C 3个 D 4个
A 1个 B 2个 C 3个 D 4个
 2 下面关于公理和定理的联系说法不正确的是( )
2 下面关于公理和定理的联系说法不正确的是( )
 A 公理和定理都是真命题,
B公理就是定理,定理也是公理,
A 公理和定理都是真命题,
B公理就是定理,定理也是公理,
 C 公理和定理都可以作为推理论证的依据D公理的正确性不需证明,定理的正确性需证明
C 公理和定理都可以作为推理论证的依据D公理的正确性不需证明,定理的正确性需证明
 3推理:如图∵ ∠AOC=∠BOD,∴∠AOC+∠AOB=∠BOD+∠AOB,这个推理的依据是( )
3推理:如图∵ ∠AOC=∠BOD,∴∠AOC+∠AOB=∠BOD+∠AOB,这个推理的依据是( )
 A 等量加等量和相等,B等量减等量差相等C 等量代换 D 整体大于部分
A 等量加等量和相等,B等量减等量差相等C 等量代换 D 整体大于部分
 4 推理:如图:∵∠A=∠ACD,∠B=∠BCD,(已知) ∴AD=CD,CD=DB(
等腰三角形的性质) ∴AD=DB( )
4 推理:如图:∵∠A=∠ACD,∠B=∠BCD,(已知) ∴AD=CD,CD=DB(
等腰三角形的性质) ∴AD=DB( )


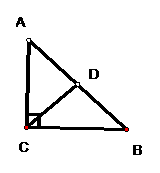
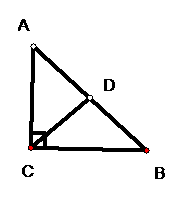 括号里应填的依据是( )
括号里应填的依据是( )
 A 旋转不改变图形的大小
A 旋转不改变图形的大小
 B 连接两点的所有线中线段最短
B 连接两点的所有线中线段最短
 C等量代换
C等量代换
 D 整体大于部分
D 整体大于部分
 5 下面定理中,没有逆定理的是
5 下面定理中,没有逆定理的是
 ( )
( )
 A 两条直线被第三条直线所
A 两条直线被第三条直线所
 截,若同位角相等,则这两条
截,若同位角相等,则这两条

|

|
 两个端点的距离相等
两个端点的距离相等
 C 平行四边形的对角线互相平分
C 平行四边形的对角线互相平分
 D对顶角相等
D对顶角相等
 二 填空题(每小题5分,共25分)
二 填空题(每小题5分,共25分)
 6 人们在长期实践中总结出来的公认的真命题,作为证明的原始依据,称这些真命题为____
6 人们在长期实践中总结出来的公认的真命题,作为证明的原始依据,称这些真命题为____
 运用基本定义和公理通过推理证明是真的命题叫_______;
运用基本定义和公理通过推理证明是真的命题叫_______;
 7定理: “直角三角形两直角边的平方和等于斜边的平方”的逆定理是:___________________
7定理: “直角三角形两直角边的平方和等于斜边的平方”的逆定理是:___________________
 _______________________________________;
_______________________________________;
 8 ____________________________________________________是定理“两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行”的逆定理
8 ____________________________________________________是定理“两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行”的逆定理
 9 如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下面结论中
9 如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下面结论中
 (1) △ABC≌△DEF,(2)∠DEF=90°,(3) AC=DF (4) AC∥DF (5) EC=CF 正确的是______________(填序号),你判断的依据是_______________________________________
(1) △ABC≌△DEF,(2)∠DEF=90°,(3) AC=DF (4) AC∥DF (5) EC=CF 正确的是______________(填序号),你判断的依据是_______________________________________


 10 要使平行四边形ABCD成为一个菱形,
10 要使平行四边形ABCD成为一个菱形,

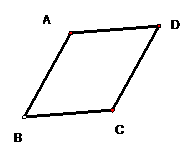 需要添加一个条件,那么你添加的是
需要添加一个条件,那么你添加的是
 _____________,依据是______
_____________,依据是______

 三 解答题(3×12+14=50分)
三 解答题(3×12+14=50分)
 11 仔细观察下面推理,
11 仔细观察下面推理,
|
 填写每一步用到的公理或定理
填写每一步用到的公理或定理

|
 CE⊥AB,E为垂足,如果∠A=125°,
CE⊥AB,E为垂足,如果∠A=125°,
 求∠BCE
求∠BCE

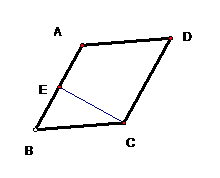 解:∵四边形ABCD是平行四边形(已知)
解:∵四边形ABCD是平行四边形(已知)
 ∴AD∥BC(
) ∵∠A=125°(已知) ∴∠B=180°-125°=55°(
∴AD∥BC(
) ∵∠A=125°(已知) ∴∠B=180°-125°=55°(
 )
)
 ∵△BEC是直角三角形(已知)∴∠BCE=90°-55°=35°(
∵△BEC是直角三角形(已知)∴∠BCE=90°-55°=35°(
 )
)

|
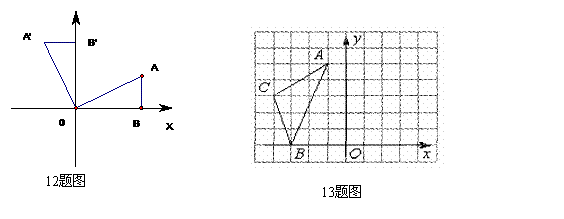
 13如图所示,在直角坐标系xOy中, A(一l,5),B(一3,0),C(一4,3).根据轴反射的定义和性质完成下面问题:(1)在右图中作出△ABC关于y轴的轴对称图形△A′B′C′;(2)写出点C关于y轴的对称点C′的坐标
13如图所示,在直角坐标系xOy中, A(一l,5),B(一3,0),C(一4,3).根据轴反射的定义和性质完成下面问题:(1)在右图中作出△ABC关于y轴的轴对称图形△A′B′C′;(2)写出点C关于y轴的对称点C′的坐标

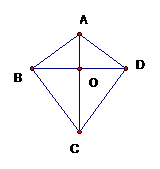 14如图,在四边形ABCD中,AB=AD,BC=DC,AC、BD相交于O,用所学公理、定理、定义说明(1)△ABC≌△ADC,(2)OB=OD,AC⊥BD
14如图,在四边形ABCD中,AB=AD,BC=DC,AC、BD相交于O,用所学公理、定理、定义说明(1)△ABC≌△ADC,(2)OB=OD,AC⊥BD






39.如图17,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米. 现以O点为原点,OM所在直线为x轴建立直角坐标系.
(1)直接写出点M及抛物线顶点P的坐标;
(2)求这条抛物线的解析式;
(3)若要搭建一个矩形“支撑架”AD- DC- CB,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长的最大值是多少?

38.某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量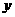 (件)与销售单价
(件)与销售单价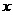 (元)符合一次函数
(元)符合一次函数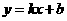 ,且
,且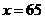 时,
时,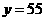 ;
;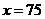 时,
时,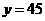 .
.
(1)求一次函数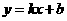 的表达式;
的表达式;
(2)若该商场获得利润为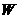 元,试写出利润
元,试写出利润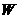 与销售单价
与销售单价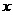 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价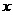 的范围.
的范围.
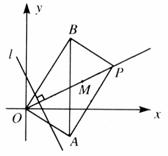
37.在坐标平面上,点P从点M(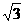 ,1)出发,沿射线OM方向以每秒1个单位长度的速度作匀速运动,在运动过程中,以OP为对角线的矩形OAPB的边长OA:OB=1:
,1)出发,沿射线OM方向以每秒1个单位长度的速度作匀速运动,在运动过程中,以OP为对角线的矩形OAPB的边长OA:OB=1: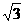 ;过点O且垂直于射线OM的直线l与点P同时出发,且与点P沿相同的方向、以相同的速度运动.
;过点O且垂直于射线OM的直线l与点P同时出发,且与点P沿相同的方向、以相同的速度运动.
(1)在点P运动过程中,试判断AB与y轴的位置关系,并说明理由;
(2)设点P与直线l都运动了t秒,求此时的矩形OAPB与直线l在运动过程中所扫过区域的重叠部分的面积S(用含t的代数式表示).
36.已知二次函数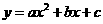 (
(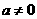 )的图象经过点
)的图象经过点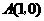 ,
,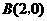 ,
,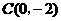 ,直线
,直线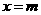 (
(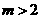 )与
)与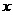 轴交于点
轴交于点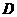 .
.
(1)求二次函数的解析式;
(2)在直线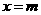 (
(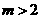 )上有一点
)上有一点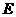 (点
(点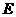 在第四象限),使得
在第四象限),使得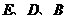 为顶点的三角形与以
为顶点的三角形与以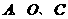 为顶点的三角形相似,求
为顶点的三角形相似,求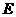 点坐标(用含
点坐标(用含 的代数式表示);
的代数式表示);
(3)在(2)成立的条件下,抛物线上是否存在一点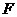 ,使得四边形
,使得四边形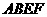 为平行四边形?若存在,请求出
为平行四边形?若存在,请求出 的值及四边形
的值及四边形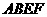 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com