
题目列表(包括答案和解析)
2.已知⊙O的周长为8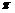 cm,若PO=2cm,则点P在_______;若PO=4cm,则点P在_____;若PO=6cm,则点P在_______.
cm,若PO=2cm,则点P在_______;若PO=4cm,则点P在_____;若PO=6cm,则点P在_______.
1.⊙O的直径为10cm,⊙O所在的平面内有一点P,当PO_______时,点P在⊙O上;当PO_____时,点P在⊙O内;当PO______时,点P在⊙O外.毛
14.某电脑公司现有A、B、C三种型号的甲品牌电脑和D、E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.
(1)写出所有选购方案;
(2)如果(1)中各种选购方案被选中的可能性相同,那么A型电脑被选中的概率是多少?
(3)现知希望中学购买甲、乙两种品牌电脑共36台(价格如图2-2-8所示),恰好用了10万元人民币,其中甲品牌电脑为A型电脑,求购买的A型电脑有几台?

13.下表是某孵鸡房对受精鸡蛋的孵化情况进行的统计:
|
受精鸡蛋数n |
1 |
4 |
40 |
100 |
200 |
1000 |
2000 |
2500 |
|
孵出小鸡数m |
1 |
|
32 |
|
168 |
961 |
|
|
|
孵出小鸡的 频率 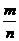 |
|
0 |
|
0.9 |
|
|
0.96 |
0.96 |
(1)填写完成表格;
(2)估计一个受精鸡蛋孵出小鸡的概率是多少?
(3)若实际需要15000只小鸡,则需要多少个受精鸡蛋?
◆拓展训练
12.张彬和王华两位同学为得到一张观看足球比赛的入场券,各自设计了一种方案:张彬:如图2-2-7,设计了一个可以自由转动的转盘,随意转动转盘,当指针指向阴影区域时,张彬得到了入场券.否则,王华得到入场券;
王华:将三个完全相同的小球分别标上数字1,2,3后,放入一个不透明袋子中,从中随机取出一个小球,然后放回袋子;混合均匀后,再随机取出一个小球.若两次取出的小球上的数字之和为偶数,王华得到入场券;否则,张彬得到入场券.
请你运用所学的概率知识,分析张彬和王华的设计方案对双方是否公平.

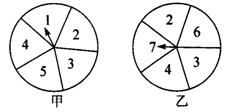
11.在如图2-2-6的甲、乙两个转盘中,指针指向每一个数字的机会是均等的,当同时转动两个转盘,停止后指的两个数字表示两条线段的长,如果第三条线段的长为5,那么这三条线段不能构成三角形的概率是( )
A.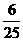 B.
B.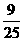 C.
C.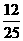 D.
D.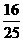
10.在□x2□2x□1的空格中,任意填上“+”、“-”,共有_____种不同的代数式,其中能构成完全平方式的占________.
9.一粒木质中国象棋子“兵”,它的正面雕刻了一个“兵”字,它的反面是平的.将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下,由于棋子的两面不均匀,为了估计“兵”字面朝上的概率,某实验小组做了棋子下掷实验,实验数据如下表:
|
实验次数 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
|
“兵”字面 朝上频数 |
14 |
|
38 |
47 |
52 |
66 |
78 |
88 |
|
相应频率 |
0.7 |
0.45 |
0.63 |
0.59 |
0.52 |
|
0.56 |
0.55 |
(1)请将数据表补充完整;
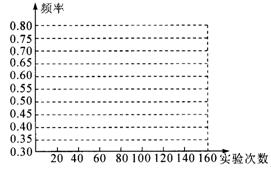
(2)在图2-2-5中画出“兵”字面朝上的频率分布折线图;
(3)如果实验继续进行下去,根据上表的数据,这个实验的频率将稳定在它的概率附近,请你估计这个概率是多少?
◆提高训练
8.王强与李刚两位同学在学习概率时,做掷骰子(均匀正方体形状)实验,他们共抛了54次,出现向上点数的次数如下表:
|
向上点数 |
1 |
2 |
3 |
4 |
5 |
6 |
|
出现次数 |
6 |
9 |
5 |
8 |
16 |
10 |
(1)请计算出现向上点数分别为3和5的频率;
(2)王强说:“根据实验,一次试验中出现向上点数为5的概率最大”.李刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”请判断王强和李刚说法的对错;(不必说明理由)
(2)如果王强和李刚各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
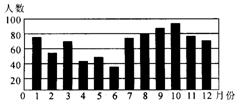
7.某校三个年级的初中在校学生共829名,学生的出生月份统计如下,根据图中数据回答以下问题:
(1)出生人数最少是几月?
(2)出生人数少于60人的月份有哪些?
(3)这些学生至少有两人生日在8月5日是可能的,不可能的,还是必然的?
(4)如果你随机地遇到这些学生中的一位,那么该学生生日在哪一个月的概率最大?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com