­1.某出版社一位编辑在设计一本书的封面时,想把封面划分为四个矩形,其中左上角矩形与右下角矩形相似(如图所示),给人一种和谐的感觉, 这样的两个相似矩形是怎样画出来的?

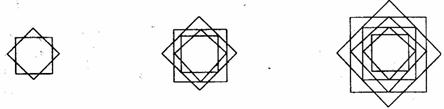
­2.如图所示,小芳用画正方形的办法画出下列一组图案, 你能按规律继续画下去吗?想想其中有哪些相似图形?

­3.用木条制成如图所示的形状,A,B,C三点钉上钉子,在D和D′处加上粉笔, 当用D′画图时,在D处的笔同时也画出一个图形,请问: 这样画上的两个图形是相似图形吗?

­三、中考题与竞赛题:(共19分)

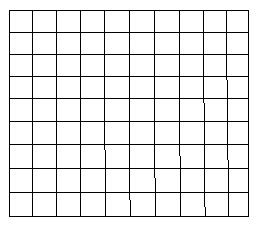
­　　 在方格纸中,每个小格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形,请你在如图所示的10×10的方格纸中,画出两个相似但不全等的格点三角形,并加以说明,要求所画的三角形是钝角三角形,并标明相应的字母.

­1.如图所示,将下列图形按相似比为3：2 画出它的相似图形.

毛

­2.如图所示,将下列图形分别分成四小块,使它们的形状、大小完全相同,并且与原图形相似,应怎样分?(画出大致图形即可)

­3.如图所示,把图(1)中的图形在图(2)中放大(形状完全一样).

4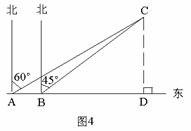．　今年入夏以来，松花江哈尔滨段水位不断下降，达到历史最低水位．一条船在松花江某水段自西向东沿直线航行，在A处测得航标C在北偏东60°的方向上．前进100米到达B处，又测得航标C在北偏东45°方向上(如图4)．在以航标C为圆心，120米长为半径的圆形区域内有浅滩．如果这条船继续前进，是否有被浅滩阻碍的危险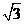？(≈1.73)．

解 　　如图，过点C作CD⊥AB，垂足为D．

在Rt△ADC中，AD＝CD·Cot∠CAD＝CD·Cot30°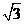＝CD．

在Rt△BDC中，AD＝CD·Cot∠CBD＝CD·Cot45°＝CD．

∴AB＝AD－BD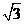＝CD－CD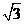＝(－1)CD＝100．

∴CD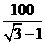＝＝50(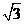+1)≈136.5(米)．

∵136.5米＞120米．∴若船继续前进没有被浅滩阻碍的危险．

3．　如图3，海中有一小岛P，在其距8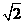海里范围内有暗礁，一轮船自西向东航行，它在A处时测得小岛P位于北偏东60°，且A、P之间的距离为16海里，若轮船继续向东方向航行，请计算轮船有无触礁的危险，如有危险，轮船自A处开始至少沿东偏南多少度方向航行，才能安全通过这一海域．

解　　 依题意画出航行图，如图3，由P向A的正东方向作垂线PB，垂足为B．

由∠PAB＝30°，得 PB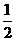＝AP＝8．

因为8＜8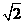，故有触礁的危险．

为了安全，应改变航行方向，并且保证P点到航向的距离不能小于暗礁的半径8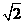，即这个距离至少等于8．

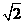设安全航向为AD，做PC⊥AD于C，由题意，AP＝16，PC＝8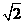，∴sin∠PAC＝．

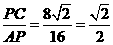∴∠PAC＝45°，从而知∠BAC＝15°．

故轮船自A开始，至少应沿东偏南15°的方向航行，才能安全通过此海域．

2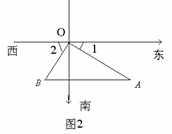．　甲、乙两船同时从港口O出发，甲船以16.1海里/小时的速度向东偏南32°方向航行，乙船向西偏南58°方向航行，航行了两小时，甲船到达A处并观测到B处的乙船恰好在其正西方向．求乙船的速度v(精确到0.1海里／小时)．　　　

(参考数据：　 sin32°＝0.53，Cos32°＝0.85，tAn32°＝0.62，Cot32°＝1.60)

分析　　 由题意知∠AOB＝90°，要求乙船的速度，得先求OB的长．

解 　　由题意可得：OA＝16．1×2＝32.2(海里)， ∠1＝32°，∠2＝58°．

∴∠AOB＝180°－(∠1+∠2)＝90°．

由B在A的正西方向，可得∠A＝∠1＝32°．

又∵在Rt△AOB中，tAnA＝，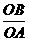

∴OB＝OA·tAnA＝32.2×0.62＝19.964．

∴v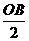＝＝19.964÷2＝9.982≈10.0(海里／小时)．

1．　台湾“华航”客机失事后，祖国大陆海上搜救中心立即通知位于A、B两处的上海救捞局所属专业救助轮“华意”轮、沪救12”轮前往出事地点协助搜救．接到通知后，“华意”轮测得出事地点C在A的南偏东60°，“沪救12”轮测得出事地点C在B的南偏东30°．已知B在A的正东方向，且相距100海里，分别求出两船到达出事地点C的距离．如图1．

分析 　　读懂题目，弄清与方位有关的词语，在△ABC中正确写出已知条件是解题的关键，依题意知△ABC是顶角为150°的等腰三角形，过点B作底边上的高，不难求出BC、AC的长．

解：作BD⊥AC，依题意知∠ABC＝120°，∠BAC＝30°，

∴BC＝AB＝100海里．在Rt△BDC中，∴∠C＝30°，

∴DC＝BC·Cos30°＝50 ．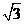

∴AC＝100．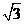

说明 　　本题是三角函数的应用问题，其实质上是用解直角三角形的知识解斜三角形的问题，如何把斜三角形的问题转化为直角三角形的问题，只要弄清题意，理解关键字词的含义，把实际问题转化为数学问题，方能正确作出辅助线，构造直角三角形求解．

22.2 过三点的圆同步练习

第1题． 经过不在同一条直线上的三点可以确定一个圆，则经过四边形ABCD的四个顶点，(　)

A．最多可作一个圆　 B．最多可作两个圆

C．最多可做三个圆　 D．最多可做四个圆

答案：A．

第2题． 已知等腰梯形ABCD，则(　)

A．它的外接圆只有一个　 B．它无外接圆

C．它的外接圆不止一个　 D．以上都不对

答案：A．

第3题． 已知Rt△ABC和Rt△ABD有公共斜边AB，若⊙O是Rt△ABC的外接圆，则⊙O是否是Rt△ABD的外接圆？

答案：⊙O是Rt△ABD的外接圆．斜边AB是Rt△ABC外接圆的直径，也是Rt△ABD外接圆的直径，同一条直径能唯一确定一个圆．

第4题． 矩形和菱形哪个有外接圆？直角梯形和等腰梯形哪个有外接圆？

答案：矩形，等腰梯形．

第5题． ⊙O的内接△ABC中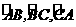，的度数之比为2∶3∶5，则∠A＝_________．

答案：54°．

第6题． 一个三角形有___________个外接圆，一个圆有___________个圆内接三角形．

答案：一，无数．

第7题． 如果圆的内接四边形的一个外角等于100°，那么它的内对角等于________度．

答案：100．

第8题． 三角形的三边分别为3，4，5，则此三角形外接圆的直径是_________．

答案：5．

第9题． 已知一条直线l的直线外两个定点A、B，经过A、B且圆心在直线l上的圆有_________个．

答案：1．

第10题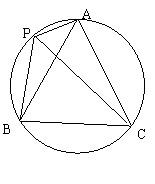． 如图，P是△ABC的外接圆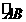上的一点，∠APC=∠BPC=60°,写出图中相等的角，并写出图中线段之间的关系(不包括比例线段)

答案：相等的角：∠BAC=∠ABC=∠ACB=∠APC=∠BPC，∠PBA=∠PCA，∠PAB=∠PCB，

边的关系：AB=BC=CA，PC=PA+PB．

第11题． 同时经过三个点可以作出的圆的个数(　)

A．只有1个　 B．只有2个　 C．有无数个 D．可能没有

答案：D．

第12题． ⊙O的内接△ABC中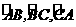，的度数之比为2∶3∶5，则∠A＝_________．

答案：54°．

第13题． 一个三角形有___________个外接圆，一个圆有___________个圆内接三角形．

答案：一，无数．

第14题． 一个三角形的外接圆的圆心叫做_______，它是_____________________的交点．

答案：外心，三角形两条边的垂直平分线．

第15题． 等边三角形的边长为1，此三角形外接圆的直径是_________．

答案：．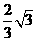

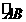第16题． 如图，P是△ABC的外接圆上的一点，∠APC=∠BPC=60°,写出图中相等的角，并写出图中线段之间的关系(不包括比例线段)

答案：相等的角：∠BAC=∠ABC=∠ACB=∠APC=∠BPC，∠PBA=∠PCA，∠PAB=∠PCB，

边的关系：AB=BC=CA，PC=PA+PB．

第17题． 以下四边形中，一定有外接圆的是(　 )

A．矩形　　 B．菱形　　 C．梯形　　 D．对角线相等的四边形

答案：A．

第18题． 下列关于确定一个圆的说法正确的是(　 )

A．经过三个点一定能确定一个圆　

B．以已知线段作为半径一定能确定一个圆

C．以已知线段作为直径一定能确定一个圆

D．经过菱形的四个顶点一定能确定一个圆

答案：C．

第19题． 直角三角形的两条直角边分别是12cm、5cm，这个三角形的外接圆的半径是(　)．

A．5cm　　 B．12cm　　 C．13cm　　 D．6．5cm

答案：D．

第20题． 下列命题中，正确的个数有(　 )

①钝角三角形没有外心；

②多边形没有外接圆；

③三角形的外心到三个顶点的距离相等；

④无论什么形状的三角形，都一定有外接圆．

A． 1个 　B．2个　 C．3个　 D．4个

答案：B．

第21题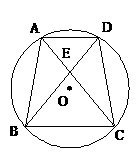． 如图，四边形ABCD是⊙O的内接四边形，且AD∥BC，对角线AC与BD交于E，那么图中有_____________对全等三角形；_____________对相似比不等于1的相似三角形．

答案：3，1．

第22题． 若线段AB=6， 则经过A、B两点的圆的半径r的取值范围是____________．

答案：．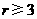

第23题． 已知Rt△ABC和Rt△ABD有公共斜边AB，若⊙O是Rt△ABC的外接圆，则⊙O是否是Rt△ABD的外接圆？

答案：⊙O是Rt△ABD的外接圆。斜边AB是Rt△ABC外接圆的直径，也是Rt△ABD外接圆的直径，同一条直径能唯一确定一个圆．

第24题． 不在同一条直线上的三点确定一个圆，“确定”的意思是_______．

答案：有且只有惟一性．

第25题． 锐角三角形的外心的位置在_________，直角三角形的外心的位置在_________，钝角三角形的外心的位置在_________．

答案：内部，斜边上，外部．

11.　 A，B，C三点表示三个村庄，为了解决村民子女就近入学的问题，计划新建一所小学，要使学校到三个村庄的距离相等，请你在途中用尺规确定学校的位置。(保留作图痕迹，不写作法)

10.　 A.1个　 B.2个　 C.3个　 D.4个

9.　　 下列命题：(1)一个圆的内接三角形有且只有一个(2)一个三角形有唯一的一个外接圆(3)过一直线上两点和它外一点可以确定一个圆(4)已知三点A，B，C，过这三点可以作并且只可以作一个圆。其中假命题的个数是(　 )