例1　 宏远广告公司要为某企业的一种产品设计商标图案，给出了如下几种初步方案，供继续设计选用(设图中圆的半径均为r)．

(1)如图1，分别以线段O₁O₂的两个端点为圆心，以这条线段的长为半径作出两个互相交错的圆的图案，试求两圆相交部分的面积．

　　 (2)如图2，分别以等边△O₁O₂O₃的三个顶点为圆心，以其边长为半径，作出三个两两相交的相同的圆，这时，这三个圆相交部分的面积又是多少呢？

　　 (3)如图3，分别以正方形O₁O₂O₃O₄的四个顶点为圆心，以其边长为半径作四个相同的圆，则这四个圆的相交部分的面积又是多少呢？(2005年黄冈市中考题)

　　 分析　 (1)利用“S_阴=S_菱形AO1BO2=4S_弓形”即可；(2)利用“S_阴=S_△O1O2O3+3S_弓”即可；(3)直接求解比较困难，可利用求补法，即“S_阴=S_{正方形O1O2O3O4}-S_空白”，考虑到四个圆半径相同，若延长O₂O­₁交⊙O₁于A，则S_空白=4S_O1AB，由(1)根据对称性可求S_O1BO4，再由“S_O1AB=S_扇形AO1O4-S_{O1BO4”，这样S空白}可求．

　　 解答　 (1)设两圆交于A、B两点，连结O₁A，O₂A，O₁B，O₂B．

　　 则S_阴=S_菱形AO1BO2+4S_弓．

　　 ∵S_菱形=2S_△AO1O2，△O₁O₂A为正△，其边长为r．

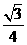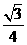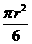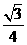　　 ∴S_△AO1O2=r²，S_弓=-r²=-r²．

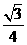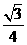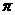　　 ∴S_阴=2×r²+4(r²-r²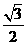)=r²-r²．

　　 (2)图2阴影部分的面积为S_阴=S_△O1O2O3+3S_弓．

　 　∵△O₁O₂O₃为正△，边长为r．

　　 ∴S_△O1O2O3=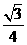r²，S_弓=-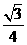r²．

　　 ∴S_阴=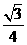r²+3(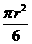-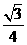r²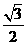)=r²-r²．

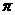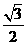　　 (3)延长O₂O₁与⊙O₁交于点A，设⊙O₁与⊙O₄交于点B，由(1)知，S_O1BO4=(r²-r²)．

　　 ∵S_O1AB=S_扇形AO1O4-S_O1BO4

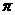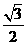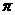　　 =-(r²=r²)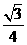

　　 =-r²+r²．

　　 则S_阴=S_{正方形O1O2O3O4}-4S_O1AB

　　 =r²-4(-r²+r²)

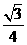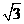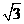　　 =r²+r²-r²=(+1-)r²．

18．如图,在钝角△ABC中,AD⊥BC,垂足为D点,且AD与DC的长度为x²-7x+12=0的两个根(AD<DC),⊙O为△ABC的外接圆,如果BD的长为6,求△ABC的外接圆⊙O的面积.

17.已知:AB是⊙O中长为4的弦,P是⊙O上一动点,cos∠APB=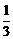, 问是否存在以A、P、B为顶点的面积最大的三角形?若不存在,试说明理由;若存在,求出这个三角形的面积.

16.要将如图所示的破圆轮残片复制完成,怎样确定这个圆轮残片的圆心和半径?(写出找圆心和半径的步骤).

15.如图,已知△ABC的一个外角∠CAM=120°,AD是∠CAM的平分线,且AD与△ABC的外接圆交于F,连接FB、FC,且FC与AB交于E.

　　 (1)判断△FBC的形状,并说明理由.

(2)请给出一个能反映AB、AC和FA的数量关系的一个等式,并说明你给出的等式成立.

14.如图,A、B、C三点表示三个工厂,要建立一个供水站, 使它到这三个工厂的距离相等,求作供水站的位置(不写作法,尺规作图,保留作图痕迹).

13.如图,已知:线段AB和一点C(点C不在直线AB上),求作:⊙O,使它经过A、B、C三点。(要求:尺规作图,不写法,保留作图痕迹)

12.平面上不共线的四点,可以确定圆的个数为(　 )

　 A.1个或3个　　　　 B.3个或4个

　 C.1个或3个或4个　 D.1个或2个或3个或4个

11.等腰直角三角形的外接圆半径等于(　 )

　 A.腰长　　　 B.腰长的倍;　　 C.底边的倍　 D.腰上的高

10.一个三角形的外心在它的内部,则这个三角形一定是(　 )

　 A.等腰三角形　　　　 B.直角三角形;　　 C.锐角三角形　　　　 D.等边三角形