
题目列表(包括答案和解析)
3.用计算器求 的按键顺序是________.
的按键顺序是________.
2.已知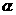 是锐角,且
是锐角,且 ,那么
,那么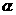 的范围是( )
的范围是( )
A. B.
B.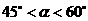
C. D.
D.
1.在 中,
中, ,
,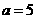 ,
, ,用计算器求
,用计算器求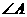 约等于( )
约等于( )
A. B.
B. C.
C. D.
D.
 例1 如图1,在
例1 如图1,在 中,
中,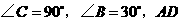
平分 .已知
.已知 ,那么
,那么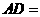 ______.
______.
析解:在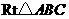 中,易知
中,易知 ,
,
 .在
.在 中,
中, ,
,
故 .
.
例2 如图2,一轮船原在 处,它的北偏东
处,它的北偏东 方向上有一灯塔
方向上有一灯塔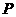 ,轮船沿着北偏西
,轮船沿着北偏西 方向航行
方向航行 小时到达
小时到达 处,这时灯塔
处,这时灯塔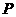 正好在轮船的正东方向上,已知轮船的航速为
正好在轮船的正东方向上,已知轮船的航速为 海里/时,求轮船在
海里/时,求轮船在 处时与灯塔
处时与灯塔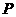 的距离.(结果可保留根号)
的距离.(结果可保留根号)

析解:如图3,构造两个直角三角形: 和
和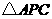 ,运用直角三角形中的边角关系求出
,运用直角三角形中的边角关系求出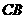 和
和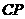 ,然后相加即可.
,然后相加即可.
 (海里),
(海里), (海里),所以
(海里),所以 海里。
海里。
锐角三角函数值的求法
基本要求:1.能够运用解直角三角形的有关知识,动手设计解决现实生活中的测量高度、长度的方案.
2.能够解决与解直角三角形有关的综合性问题和探索性问题.
基本要求:1.掌握仰角、俯角、坡角、坡度、方位角等概念.
2.能根据题意在所给的图形(或根据题意自己画出图形)中恰当地构造直角三角形,运用解直角三角形(有时还需要借助方程)的有关知识解决实际问题.
例1 (北京西城区中考题)若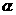 为锐角,
为锐角, ,则
,则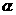 =__.
=__.
解:由公式①可知,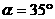 .
.
例2 (包头市中考题)已知在Rt△ABC中,∠C=90°, ,则
,则 =( )
=( )
A. B.
B. C.
C. D.
D.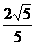
解:∵ ,∠B是锐角,
,∠B是锐角, >0,由公式①,得
>0,由公式①,得
∴ =
= ,所以,选(B).
,所以,选(B).
例3 (山西省中考题)计算:
 =_____.
=_____.
分析:因为48°+42°=90°,44°+46°=90°,
所以有: ,
, =1.
=1.
解:原式=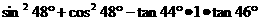 =1-1=0.
=1-1=0.
锐角三角形函数应用
 如右图,在Rt△ABC中,∠C=90°,由三角函数的定义可得:
如右图,在Rt△ABC中,∠C=90°,由三角函数的定义可得:
 ,
, ,
,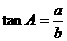 ,
,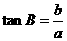 ,则有:
,则有:
(1)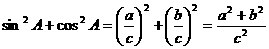
由勾股定理,得:a2+b2=c2,所以,有:sin2A+cos2A=1 ①
(2)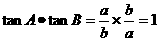
 ②
②
说明:(1)当∠A+∠B=90°时,因为sinB= ,
,
所以此时又有sin2A+sin2B=1.
(2)公式②成立的条件是∠A+∠B=90°.
例4 如图4, 在Rt△ABC中,ACB=90,CD⊥AB于点D,BC=3,AC=4,设BCD=α,tanα的值为( )
 (A)
(A)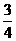 (B)
(B)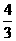 (C)
(C)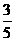 (D)
(D)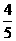
分析:由三角形函数的定义知tanα= ,
,
由Rt△CDB∽Rt△ACB,
所以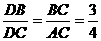 ,所以tanα=
,所以tanα=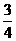 ,选(A).
,选(A).
三角函数中的两个关系式
 例3 如图3,CD是平面镜,光线从A点出发经CD上点E反射后照射到B点,若入射角为
例3 如图3,CD是平面镜,光线从A点出发经CD上点E反射后照射到B点,若入射角为 (入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=11,则tan
(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=11,则tan 的值为( )
的值为( )
(A) (B)
(B) (C)
(C)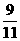 (D)
(D)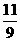
分析:根据已知条件可得∠α=∠CAE,所以只需求出tan∠CAE.
根据条件可知△ACE∽△BDE,所以 ,即
,即 ,
,
所以CE= ,在Rt△AEC中,tan∠CAE=
,在Rt△AEC中,tan∠CAE=
 .
.
所以tan =
=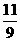 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com