
题目列表(包括答案和解析)
6.等腰三角形的腰长为2cm,面积为1 cm2,则顶角的度数为
5.已知△ABC中,∠B=30°,a=2,c=3,则S△ABC=
4.已知正六边形的面积为3cm2,则它的外接圆半径为
3.半径为10cm的圆内接正三角形的边长为 ,内接正方形的边长为 ,内接正六边形的边长为
2.在Rt△ABC中,AD是斜边BC上的高,如果BC=a,∠B=α,那么AD等于( )
(A)asin2α (B)acos2α (C)asinαcosα (D)asinαtanα
1.△ABC中,∠C=90°,根据表中的数据求其它元素的值:
|
a |
B |
c |
∠A |
∠B |
|
|
|
12 |
30° |
|
|
|
4 |
|
|
45° |
|
|
|
|
|
60° |
|
5 |
5 |
|
|
|
|
|
4 |
8 |
|
|
4.3解直角三角形及其应用
[预习练习]
25.3解直角三角形
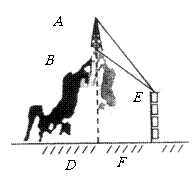 第1题.如图,在观测点
第1题.如图,在观测点 测得小山上铁塔顶
测得小山上铁塔顶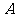 的仰角为
的仰角为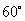 ,铁塔底部
,铁塔底部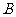 的仰角为
的仰角为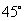 .已知塔高
.已知塔高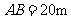 ,观测点
,观测点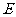 到地面的距离
到地面的距离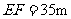 ,求小山
,求小山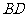 的高(精确到
的高(精确到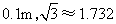 ).
).
答案:解:如图,过点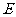 作
作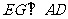 于点
于点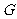 .
.
由已知,得
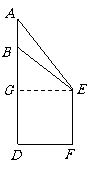
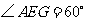 ,
,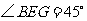 .
.
在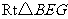 中,
中,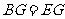 .
.
在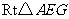 中,由
中,由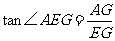 ,得
,得
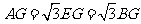 ,
,
又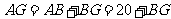 ,
,
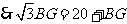 ,即
,即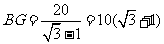 .
.

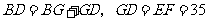 ,
,
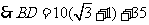
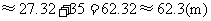 .
.
答:小山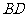 的高约为
的高约为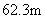 .
.
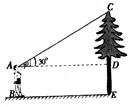 第2题.如图,身高1.6m的小丽用一个两锐角分别为
第2题.如图,身高1.6m的小丽用一个两锐角分别为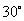 和
和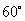 的三角尺测量一棵树的高度,已知她与树之间的距离为6m,那么这棵树高大约为 .(结果精确到0.1m,其中
的三角尺测量一棵树的高度,已知她与树之间的距离为6m,那么这棵树高大约为 .(结果精确到0.1m,其中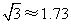 ,小丽眼睛距离地面高度近似为身高)
,小丽眼睛距离地面高度近似为身高)
答案:5.1m
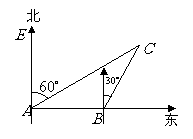
第3题.某船以每小时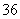 海里的速度向正东方向航行,在点
海里的速度向正东方向航行,在点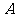 测得某岛
测得某岛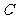 在北偏东
在北偏东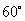 方向上,航行半小时后到达点
方向上,航行半小时后到达点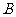 ,测得该岛在北偏东
,测得该岛在北偏东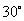 方向上,已知该岛周围
方向上,已知该岛周围 海里内有暗礁
海里内有暗礁
 (1)试说明点
(1)试说明点 是否在暗礁区域外?
是否在暗礁区域外?
(2)若继续向东航行有无触礁危险?请说明理由.
答案:(1)过点 作
作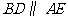 ,交
,交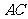 于点
于点
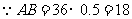 (海里)
(海里)
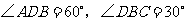

又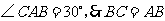
即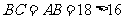
 点
点 在暗礁区域外
在暗礁区域外
(2)过点 作
作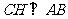 ,垂足为
,垂足为
在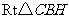 中,
中,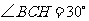
令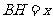 ,则
,则
在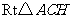 中,
中,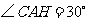

 ,
,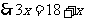
解得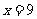

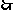 船继续向东航行有触礁的危险
船继续向东航行有触礁的危险
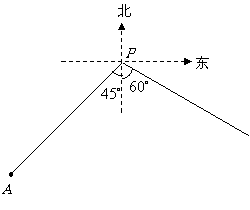
第4题.如图,小岛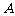 在港口
在港口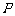 的南偏西
的南偏西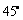 方向,距离港口81海里处.甲船从
方向,距离港口81海里处.甲船从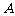 出发,沿
出发,沿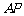 方向以9海里/时的速度驶向港口,乙船从港口
方向以9海里/时的速度驶向港口,乙船从港口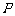 出发,沿南偏东
出发,沿南偏东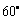 方向,以18海里/时的速度驶离港口.现两船同时出发,
方向,以18海里/时的速度驶离港口.现两船同时出发,
(1)出发后几小时两船与港口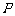 的距离相等?
的距离相等?
(2)出发后几小时乙船在甲船的正东方向?(结果精确到0.1小时)(参考数据: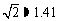 ,
,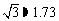 )
)
答案:解:(1)设出发后 小时两船与港口
小时两船与港口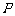 的距离相等.
的距离相等.
根据题意,得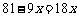 .
.
解这个方程,得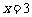 .
.
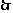 出发后3小时两船与港口
出发后3小时两船与港口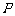 的距离相等.
的距离相等.
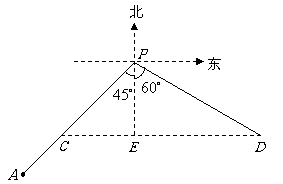
(2)设出发后 小时乙船在甲船的正东方向.此时甲、乙两船的位置分别在点
小时乙船在甲船的正东方向.此时甲、乙两船的位置分别在点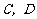 处.连接
处.连接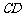 .过点
.过点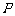 作
作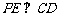 ,垂足为
,垂足为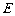 .则点
.则点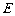 在点
在点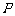 的正南方向.
的正南方向.
在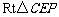 中,
中,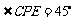 ,
,
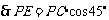 .
.
在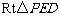 中,
中,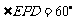 ,
,
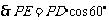 .
.
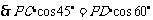 .
.
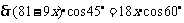 .
.
解这个方程,得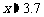 .
.
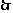 出发后约3.7小时乙船在甲船的正东方向.
出发后约3.7小时乙船在甲船的正东方向.
第5题.如图,在一个坡角为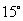 的斜坡上有一棵树,高为
的斜坡上有一棵树,高为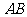 .当太阳光与水平线成
.当太阳光与水平线成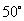 时,测得该树在斜坡上的树影
时,测得该树在斜坡上的树影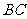 的长为
的长为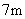 ,求树高.(精确到
,求树高.(精确到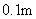 )
)
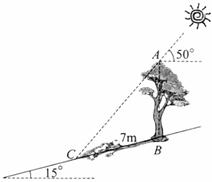
答案:解:如图,过点 作水平线与
作水平线与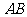 的延长线交于点
的延长线交于点 ,则
,则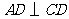 .
.
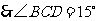 ,
, .分
.分
在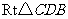 中,
中,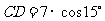 ,
,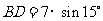 .
.
 在
在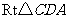 中,
中,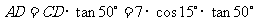 .
.
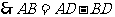
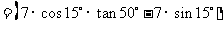
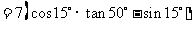
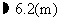 .
.
答:树高约为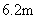 .
.
第6题.如图,某市郊外景区内一条笔直的公路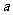 经过三个景点
经过三个景点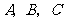 .景区管委会又开发了风景优美的景点
.景区管委会又开发了风景优美的景点 .经测量景点
.经测量景点 位于景点
位于景点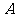 的北偏东
的北偏东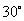 方向
方向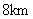 处,位于景点
处,位于景点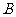 的正北方向,还位于景点
的正北方向,还位于景点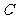 的北偏西
的北偏西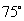 方向上.已知
方向上.已知 .
.
(1)景区管委会准备由景点 向公路
向公路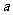 修建一条距离最短的公路,不考虑其他因素,求出这条公路的长.(结果精确到0.1km)
修建一条距离最短的公路,不考虑其他因素,求出这条公路的长.(结果精确到0.1km)
(2)求景点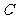 与景点
与景点 之间的距离.(结果精确到1km)
之间的距离.(结果精确到1km)
(参考数据: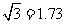 ,
,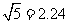 ,
,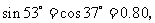
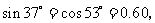
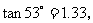
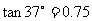 ,
,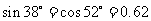 ,
, ,
,

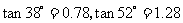 ,
,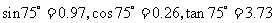 .)
.)
答案:解:(1)如图,过点 作
作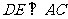 于点
于点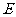 ,
,
过点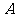 作
作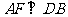 ,交
,交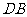 的延长线于点
的延长线于点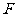 .
.
在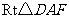 中,
中,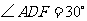 ,
,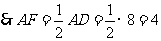 .
.
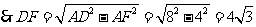 .
.
 在
在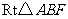 中,
中,
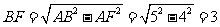 .
.
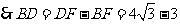 .
.
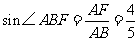 .
.
在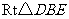 中,
中,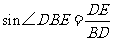 ,
,
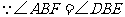 ,
,
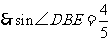 .
.
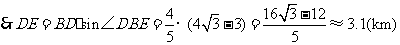 .
.
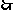 景点
景点 向公路
向公路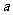 修建的这条公路的长约是3.1km.
修建的这条公路的长约是3.1km.
(2)由题意可知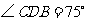 ,
,
由(1)可知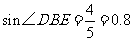 ,所以
,所以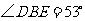 ,
,
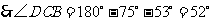 ,
,
在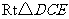 中,
中,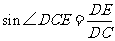 ,
,
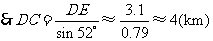 .
.
 景点
景点 与景点
与景点 之间的距离约为4km.
之间的距离约为4km.
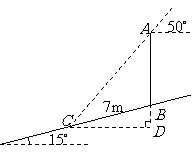
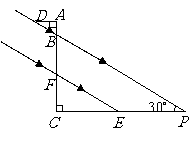
第7题. 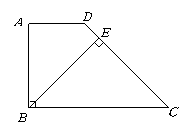 已知:如图,在梯形
已知:如图,在梯形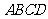 中,
中,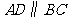 ,
,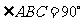 ,
,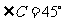 ,
,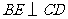 于点
于点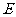 ,
,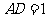 ,
,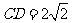 .
.
求: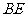 的长.
的长.
解:答案:解:如图,过点 作
作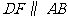 交
交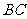 于点
于点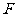 .
.
因为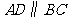 ,
,
所以四边形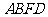 是平行四边形.
是平行四边形.
 所以
所以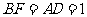 .
.
由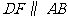 ,
,
得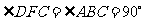 .
.
在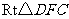 中,
中,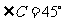 ,
,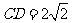 ,
,
由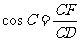 ,
,
求得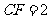 .
.
所以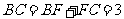 .
.
在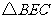 中,
中,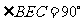 ,
,
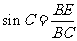 .
.
求得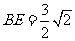 .
.
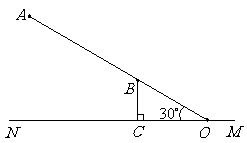
第8题.如图所示,在一笔直的公路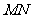 的同一旁有两个新开发区
的同一旁有两个新开发区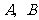 ,已知
,已知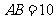 千米,直线
千米,直线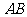 与公路
与公路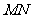 的夹角
的夹角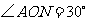 ,新开发区
,新开发区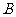 到公路
到公路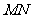 的距离
的距离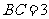 千米.
千米.
(1)求新开发区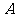 到公路
到公路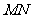 的距离;
的距离;
 (2)现要在
(2)现要在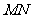 上某点
上某点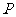 处向新开发区
处向新开发区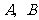 修两条公路
修两条公路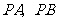 ,使点
,使点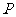 到新开发区
到新开发区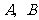 的距离之和最短.请你用尺规作图在图中找出点
的距离之和最短.请你用尺规作图在图中找出点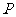 的位置(不用证明,不写作法,保留作图痕迹),并求出此时
的位置(不用证明,不写作法,保留作图痕迹),并求出此时 的值.
的值.
答案:解:(1)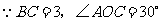 ,
,
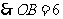
过点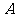 作
作 于点
于点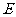 ,
,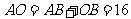 ,
,
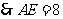 .
.
即新开发区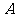 到公路的距离为
到公路的距离为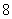 千米.
千米.
(2)画图正确.
过 作
作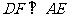 的延长线(点
的延长线(点 是点
是点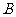 关于
关于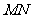 的对称点),垂足为
的对称点),垂足为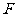 ,则
,则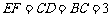
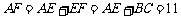
过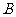 作
作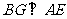 于
于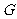
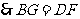
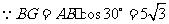
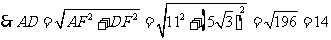 ,
,
连结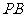 ,则
,则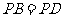 ,
,
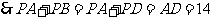 (千米).
(千米).
第9题.如图,在某建筑物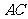 上,挂着“多彩贵州”的宣传条幅
上,挂着“多彩贵州”的宣传条幅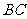 ,小明站在点
,小明站在点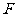 处,看条幅顶端
处,看条幅顶端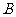 ,测得仰角为
,测得仰角为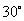 ;再往条幅方向前行
;再往条幅方向前行 米到达点
米到达点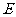 处,看条幅顶端
处,看条幅顶端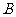 ,测得仰角为
,测得仰角为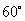 .求宣传条幅
.求宣传条幅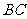 的长.(小明的身高忽略不计,结果精确到
的长.(小明的身高忽略不计,结果精确到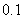 米)
米)

答案:解: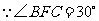 ,
,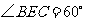 ,
,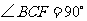 ,
,
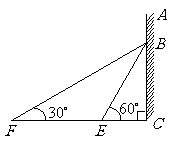
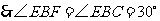 ,
,
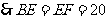 .
.
在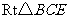 中,
中,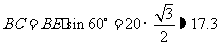 (
(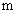 )
)
答:宣传条幅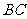 的长约为
的长约为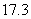 米.
米.
第10题.菏泽市在城市建设中,要折除旧烟囱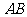 (如图所示),在烟囱正西方向的楼
(如图所示),在烟囱正西方向的楼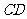 的顶端
的顶端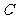 ,测得烟囱的顶端
,测得烟囱的顶端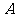 的仰角为
的仰角为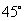 ,底端
,底端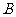 的俯角为
的俯角为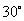 ,已量得
,已量得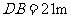 .
.
(1)在原图上画出点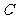 望点
望点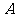 的仰角和点
的仰角和点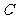 望点
望点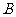 的俯角,并分别标出仰角和俯角的大小.
的俯角,并分别标出仰角和俯角的大小.
(2)拆除时若让烟囱向正东倒下,试问:距离烟囱东方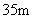 远的一棵大树是否被歪倒的烟囱砸着?请说明理由.
远的一棵大树是否被歪倒的烟囱砸着?请说明理由.

答案: 解:(1)
解:(1)
(2)在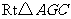 中,
中,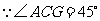 .
.
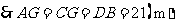 ,
,
在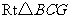 中,
中,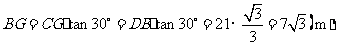 ,
,
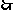 烟囱高
烟囱高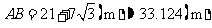 ,
,
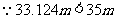 ,
,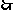 这棵大树不会被歪倒的烟囱砸着.
这棵大树不会被歪倒的烟囱砸着.
第11题.如图,某一时刻太阳光从教室窗户射入室内,与地面的夹角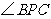 为
为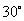 ,窗户的一部分在教室地面所形成的影长
,窗户的一部分在教室地面所形成的影长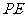 为
为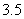 米,窗户的高度
米,窗户的高度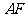 为
为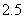 米.求窗外遮阳蓬外端一点
米.求窗外遮阳蓬外端一点 到窗户上椽的距离
到窗户上椽的距离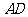 .(结果精确
.(结果精确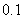 米)
米)
答案:方法一:
过点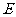 作
作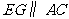 交
交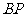 于点
于点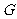 ,
,
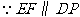
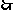 四边形
四边形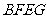 是
是 ,
,
在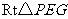 中,
中,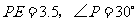 ,
,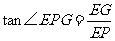
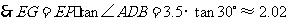 (或
(或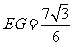 )
)
又 四边形
四边形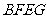 是
是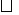 ,
,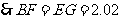
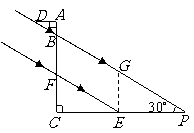
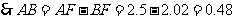 (或
(或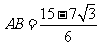 )
)
又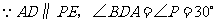 ,
,
在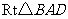 中,
中,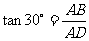 ,
,
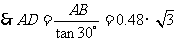 (或
(或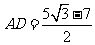 )
)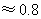 ,
,
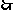 所求的距离
所求的距离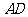 约为
约为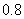 米.
米.
方法二:
在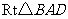 中,设
中,设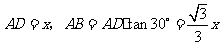 ,
,
在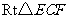 中,设
中,设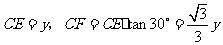 ,
,
在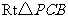 中,
中,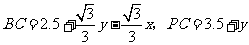
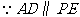
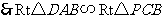
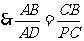
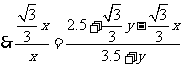 化简得:
化简得: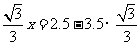
解答: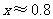 (米)
(米)
方法三:
过点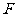 作
作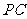 的平行线,
的平行线,
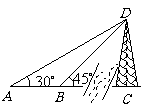 第12题.小红同学想测量河对岸一通信塔的高度,她先在点
第12题.小红同学想测量河对岸一通信塔的高度,她先在点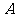 处测得塔顶
处测得塔顶 的仰角为
的仰角为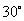 ,这时她再往正前方前进20米到点
,这时她再往正前方前进20米到点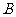 ,又测得塔顶
,又测得塔顶 的仰角为
的仰角为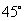 ,请你帮她算一算塔
,请你帮她算一算塔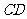 的高(答案保留根号).
的高(答案保留根号).
答案:解:设塔高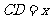 米,则
米,则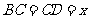 米
米
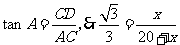 .
.
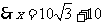 .
.
答:塔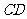 的高为
的高为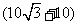 米.
米.
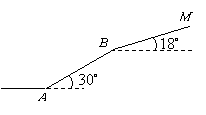
第13题.某科技馆座落在山坡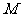 处,从山脚
处,从山脚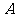 处到科技馆的路线如图所示.已知
处到科技馆的路线如图所示.已知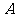 处海拔高度为
处海拔高度为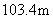 ,斜坡
,斜坡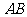 的坡角为
的坡角为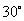 ,
,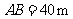 ,斜坡
,斜坡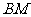 的坡角为
的坡角为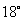 ,
,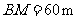 ,那么科技馆
,那么科技馆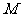 处的海拔高度是多少?(精确到
处的海拔高度是多少?(精确到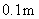 )
)
 (参考数据:
(参考数据: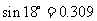
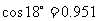
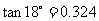
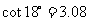 )
)
答案:解:过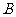 向水平线
向水平线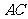 作垂线
作垂线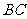 ,垂足为
,垂足为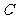 ,过
,过 向水平线
向水平线 作垂线
作垂线 ,垂足为
,垂足为 (如右图),则
(如右图),则
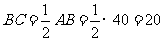 .
.
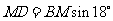
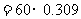
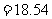 .
.
 科技馆
科技馆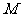 处的海拔高度是:
处的海拔高度是: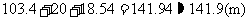 .
.
 第14题.如图,小鹏准备测量学校旗杆的高度.他发现当斜坡正对着太阳时,旗杆
第14题.如图,小鹏准备测量学校旗杆的高度.他发现当斜坡正对着太阳时,旗杆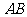 的影子恰好落在水平地面
的影子恰好落在水平地面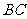 和斜坡坡面
和斜坡坡面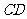 上,测得旗杆在水平地面上的影长
上,测得旗杆在水平地面上的影长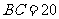 米,在斜坡坡面上的影长
米,在斜坡坡面上的影长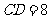 米,太阳光线
米,太阳光线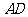 与水平地面成
与水平地面成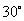 角,且太阳光线
角,且太阳光线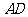 与斜坡坡面
与斜坡坡面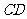 互相垂直.请你帮小鹏求出旗杆
互相垂直.请你帮小鹏求出旗杆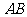 的高度(精确到1米).
的高度(精确到1米).
(可供选用数据:取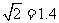 ,
,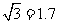 )
)
答案:解:延长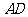 ,
,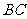 相交于点
相交于点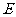 ,则
,则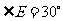 ,,
,,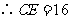 .
.
在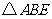 A中,
A中,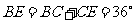 ,由
,由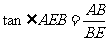 ,
,
得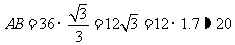
答:
 第15题.为测量某塔
第15题.为测量某塔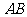 的高度,在离该塔底部20米处目测其顶,仰角为
的高度,在离该塔底部20米处目测其顶,仰角为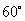 ,目高1.5米,试求该塔的高度
,目高1.5米,试求该塔的高度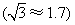 .
.
答案:解:如图所示,过点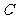 作
作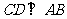 ,交
,交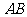 于点
于点 .
.
在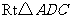 中,
中,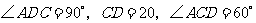 ,
,
所以,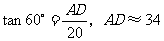 .
.
所以,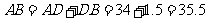 (米).
(米).
所以,该塔的高度是35.5米.
第16题.如图,某市郊外景区内一条笔直的公路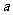 经过三个景点
经过三个景点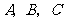 .景区管委会又开发了风景优美的景点
.景区管委会又开发了风景优美的景点 .经测量景点
.经测量景点 位于景点
位于景点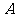 的北偏东
的北偏东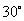 方向
方向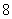 千米处,位于景点
千米处,位于景点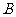 的正北方向,还位于景点
的正北方向,还位于景点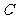 的北偏西
的北偏西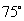 方向上.已知
方向上.已知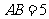 千米.
千米.
(1)景区管委会准备由景点 向公路
向公路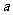 修建一条距离最短的公路,不考虑其他因素,求出这条公路的长;(结果精确到0.1千米)
修建一条距离最短的公路,不考虑其他因素,求出这条公路的长;(结果精确到0.1千米)
 (2)求景点
(2)求景点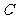 与景点
与景点 之间的距离.(结果精确到1千米)
之间的距离.(结果精确到1千米)
(参考数据: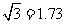 ,
,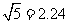 ,
,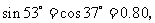
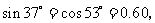
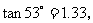
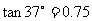 ,
,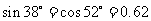 ,
, ,
,
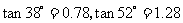 ,
,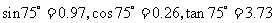 .)
.)
答案:解:(1)如图1,过点 作
作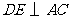 于点
于点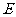
过点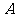 作
作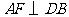 ,交
,交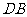 的延长线于点
的延长线于点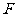
在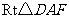 中,
中,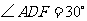 ,
,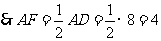

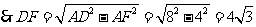
在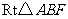 中
中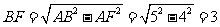
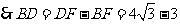
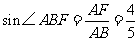
在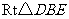 中,
中,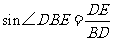
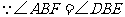
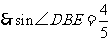
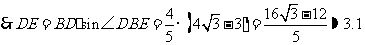 (千米)
(千米)
答:景点 向公路
向公路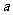 修建的这条公路的长约是
修建的这条公路的长约是 千米
千米
(2)由题意可知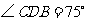
由(1)可知 ,所以
,所以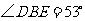
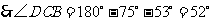
在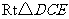 中,
中,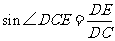
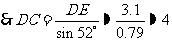 (千米)
(千米)
答:景点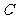 与景点
与景点 之间的距离约为
之间的距离约为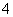 千米
千米
第17题.小明想测量校园内一棵不可攀的树的高度.由于无法直接度量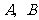 两点间的距离,请你用学过的数学知识按以下要求设计一种测量方案.
两点间的距离,请你用学过的数学知识按以下要求设计一种测量方案.
(1)画出测量图案;
(2)写出测量步骤(测量数据用字母表示);
(3)计算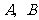 间的距离(写出求解或推理过程,结果用字母表示).
间的距离(写出求解或推理过程,结果用字母表示).
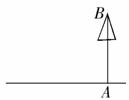
答案:(1)答案不唯一,提供一种方案:
 测量平面图如图:
测量平面图如图:
(2)测量出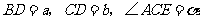
(3)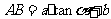 .
.
第18题.如图,某人在山坡坡脚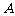 处测得电视塔尖点
处测得电视塔尖点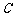 的仰角为
的仰角为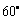 ,沿山坡向上走到
,沿山坡向上走到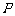 处再测得点
处再测得点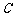 的仰角为
的仰角为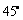 ,已知
,已知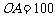 米,山坡坡度为
米,山坡坡度为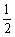 (即
(即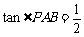 )且
)且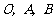 在同一条直线上.求电视塔
在同一条直线上.求电视塔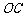 的高度以及此人所在位置点
的高度以及此人所在位置点 的铅直高度.(测倾器的高度忽略不计,结
的铅直高度.(测倾器的高度忽略不计,结
5、(安徽03/21)如图是五角星,已知AC=a,求五角星外接圆的直径(结果用含三角函数的式子表示)。
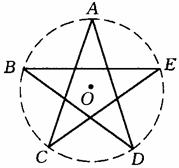
[解]

4、如图,在△ABC中,已知∠ACB=90°,CD⊥AB于D,AC=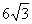 ,BD=3。
,BD=3。
(1)请根据下面求cosA的解答过程,在横线上填上适当的结论,使解答正确完整:
∵CD⊥AB ∠ACB=90°
∴AC= AB cosA, AD =AC·cosA
由已知AC=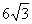 ,BD=3
,BD=3
∴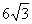 =AB cosA=(AD+BD)cosA=(
=AB cosA=(AD+BD)cosA=(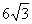 cosA+3)cosA
cosA+3)cosA
设t=cosA,则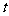 >0,且上式可化为
>0,且上式可化为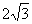
 +t-
+t-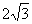 =0,则此解得cosA=
=0,则此解得cosA=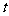 =
=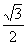
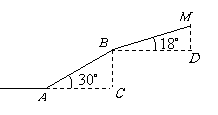
(2)求BC的长及△ABC的面积。

(2)解:在Rt△ABC中,BC=AC·tanA=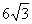 ·
·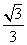 =6
=6
S△ABC=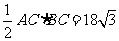
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com