3.先指出下列方程用哪种方法来解比较合适，然后再按这种方法解：

　 (1)(2x-3)²=25；

　 (2)(2x-3)²=5(2x-3)；

　 (3)(2x-3)=x(3x-2).

2.指出下列方程用哪种方法来解比较适当：

　 (1)(2x+3)²=-2x；

　 (2)(2x+3)²=4(2x+3)；

　 (3)(2x+3)²=6.

2.完成下面的解题过程：

　 (1)用直接开平方法解方程：2(x-3)²-6=0；

解：原方程化成　　　　　　　　　　　 .

开平方，得　　　　　　　　　　 ，

x₁=　　　 ，x₂=　　　 .

(2)用配方法解方程：3x²-x-4=0；

解：移项，得　　　　　　　　　　 .

　　 二次项系数化为1，得　　　　　　　　　 .

　　 配方　　　　　　　　　　　　　　　 ，

　　　　 　　　　　　　　　　　　.

　　 开平方，得　　　　　　　　　　　　 ，

　　　　　 x₁=　　　 ，x₂=　　　 .

　(3)用公式法解方程：x(2x-4)=2.5-8x.

解：整理，得 　　　　　　　　　　　.

a=　　　 ，b=　　　 ，c=　　　 .

　　 b²-4ac=　　　　　　　　　　 =　　　 ＞0.

　　 ,

　　　　　 x₁=　　　 ，x₂=　　　 .

(4)用因式分解法解方程：x(x+2)=3x+6.

解：移项，得　　　　　　　　　　　 .

　　 因式分解，得　　　　　　　　　　　 .

　　 于是得　　　　　　　　 或　　　　　　　　 ，

　　　　　 x₁=　　　 ，x₂=　　　 .

1.填空：解一元二次方程的方法有四种，它们是直接开平方法、　　　　　　 、

　 　　　　　　　、　　　　　　　　　　 .

3.用因式分解法解下列方程：

　 (1)x²+x=0；

　 (2)4x²-121=0；

　(3)3x(2x+1)=4x+2；

　 (4)(x-4)²=(5-2x)².

第6课时

2.完成下面的解题过程：

　 用因式分解法解方程：x²=2x.

解：移项，得　　　　　　　　　　　 .

因式分解，得　　　　　　　　　　 .

于是得　　　　　　　 或　　　　　　　 ，

　　　 x₁=　　　 ，x₂=　　　 .

1.完成下面的解题过程：

　 用公式法解方程：2x(x-1)+6=2(0.5x+3)

解：整理，得　　　　　　　　　　　　 .

a=　　　 ，b=　　　 ，c=　　　 .

　　 b²-4ac=　　　　　　　　　　 =　　　 ＞0.

　　 ，

　　 ，.

2.利用判别式判断下列方程的根的情况：

　 (1)x²-5x=-7；

　 (2)(x-1)(2x+3)=x；

　 (3)x²+5=2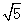x.

第5课时

1.完成下面的解题过程：

　 用公式法解下列方程：

(1)2x²-3x-2=0.

解：a=　　　 ，b=　　　 ，c=　　　 .

　　 b²-4ac=　　　　　　　　 =　　　 ＞0.

　　 ，

　　 ，.

(2)x(2x-)=x-3.

解：整理，得　　　　　　　　　　　 .

a=　　　 ，b=　　　 ，c=　　　 .

　　 b²-4ac=　　　　　　　　 =　　　 .

　　 ，

　　 .

(3)(x-2)²=x-3.

解：整理，得　　　　　　　　　　　 .

a=　　　 ，b=　　　 ，c=　　　 .

　　 b²-4ac=　　　　　　　　　 =　　　 ＜0.

　　 方程　　　　 实数根.

3.用配方法解方程：(2x+1)(x-3)=x-9.

第4课时