
题目列表(包括答案和解析)
4.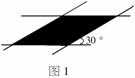 如图1,若两条宽度为1的带子相交成30°的角,则重叠部分(图中阴影部分)的面积是( )
如图1,若两条宽度为1的带子相交成30°的角,则重叠部分(图中阴影部分)的面积是( )
A.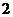 B.
B.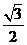 C.
C.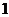 D.
D.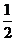
3.已知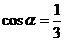 ,则
,则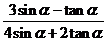 的值等于( )
的值等于( )
A.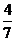 B.
B.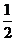 C.
C.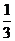 D.
D.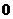
2.如果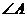 是锐角,且
是锐角,且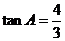 ,那么( )
,那么( )
A.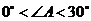 B.
B.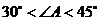
C.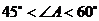 D.
D.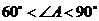
1.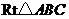 中,
中,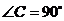 ,
,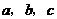 分别
分别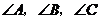 的对边,下列关系中错误的是( )
的对边,下列关系中错误的是( )
A.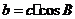 B.
B.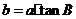 C.
C.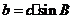 D.
D.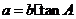
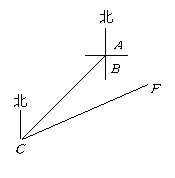
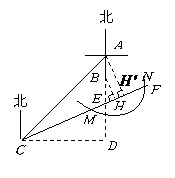
如图,某乡村小学有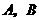 两栋教室,
两栋教室, 栋教室在
栋教室在 栋教室正南方向36米处,在
栋教室正南方向36米处,在 栋教室西南方向
栋教室西南方向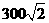 米的
米的 处有一辆拖拉机以每秒8米的速度沿北偏东
处有一辆拖拉机以每秒8米的速度沿北偏东 的方向
的方向 行驶.若拖拉机的噪声污染半径为
行驶.若拖拉机的噪声污染半径为 米,试问
米,试问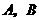 两栋教室是否受到拖拉机噪声的影响?若有影响,影响的时间有多少秒?(计算过程中
两栋教室是否受到拖拉机噪声的影响?若有影响,影响的时间有多少秒?(计算过程中 取
取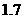 ,各步计算结果精确到整数)
,各步计算结果精确到整数)
 答案:解:过点
答案:解:过点 作直线
作直线 的垂线,垂足为
的垂线,垂足为 .
.
设拖拉机行驶路线 与
与 交于点
交于点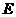 ,
,
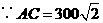 ,
,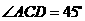 ,
,
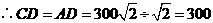 .
.
在 中,
中,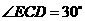 ,
,
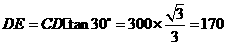 .
.
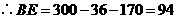 .
.
过点 作
作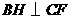 ,垂足为
,垂足为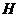 ,则
,则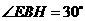 .
.
21.(12分)如图,小岛 在港口
在港口 的南偏西
的南偏西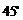 方向,距离港口81海里处.甲船从
方向,距离港口81海里处.甲船从 出发,沿
出发,沿 方向以9海里/时的速度驶向港口,乙船从港口
方向以9海里/时的速度驶向港口,乙船从港口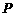 出发,沿南偏东
出发,沿南偏东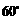 方向,以18海里/时的速度驶离港口.现两船同时出发,
方向,以18海里/时的速度驶离港口.现两船同时出发,
(1)出发后几小时两船与港口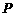 的距离相等?
的距离相等?
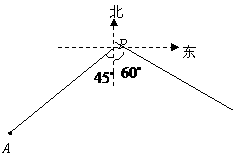 (2)出发后几小时乙船在甲船的正东方向?(结果精确到0.1小时)(参考数据:
(2)出发后几小时乙船在甲船的正东方向?(结果精确到0.1小时)(参考数据: ,
,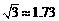 )
)
答案:解:(1)设出发后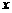 小时两船与港口
小时两船与港口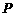 的距离相等.
的距离相等.
根据题意,得 .
.
解这个方程,得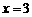 .
.
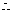 出发后3小时两船与港口
出发后3小时两船与港口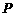 的距离相等.
的距离相等.
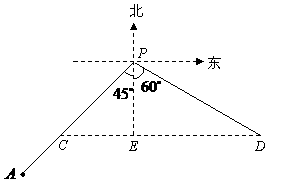 (2)设出发后
(2)设出发后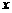 小时乙船在甲船的正东方向.此时甲、乙两船的位置分别在点
小时乙船在甲船的正东方向.此时甲、乙两船的位置分别在点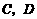 处.连接
处.连接 .过点
.过点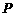 作
作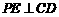 ,垂足为
,垂足为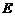 .则点
.则点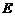 在点
在点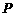 的正南方向.
的正南方向.
在 中,
中,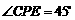 ,
,
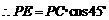 .
.
在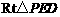 中,
中,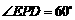 ,
,
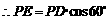 .
.
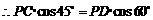 .
.
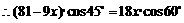 .
.
解这个方程,得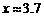 .
.
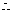 出发后约3.7小时乙船在甲船的正东方向.
出发后约3.7小时乙船在甲船的正东方向.
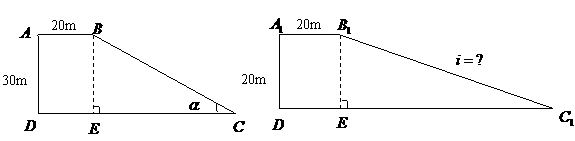
20.(12分)一段路基的横断面是直角梯形,如左下图所示,已知原来坡面的坡角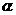 的正弦值为0.6,现不改变土石方量,全部利用原有土石方进行坡面改造,使坡度变小,达到如右下图所示的技术要求.试求出改造后坡面的坡度是多少?
的正弦值为0.6,现不改变土石方量,全部利用原有土石方进行坡面改造,使坡度变小,达到如右下图所示的技术要求.试求出改造后坡面的坡度是多少?
答案:解:
 由左图可知:
由左图可知: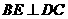 ,
,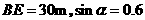 ,
,
在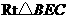 中,
中,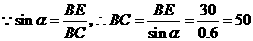 (m).
(m).
由勾股定理得,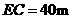 .
.
在不改变土石方量,全部充分利用原有土石方的前提下进行坡面改造,使坡度变小,则梯形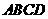 面积
面积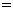 梯形
梯形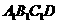 面积.
面积.
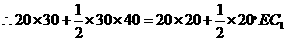 ,
,
解得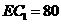 (m).
(m).
 改建后的坡度
改建后的坡度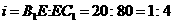 .
.
19. (12分)如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为
(12分)如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为 ,此人以每秒
,此人以每秒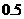 米收绳.问:
米收绳.问: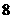 秒后船向岸边移动了多少米?(结果精确到
秒后船向岸边移动了多少米?(结果精确到 米)
米)
答案:设8秒后船移动到点 ,在
,在 中,
中,
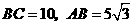
在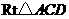 中,
中,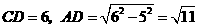
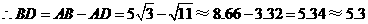 .
.
答:船向岸边移动了5.3米.
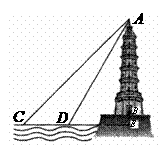
18.(12分)某中学初三(2)班数学活动小组利用周日开展课外实践活动,他们要在湖面上测量建在地面上某塔 的高度.如图,在湖面上点
的高度.如图,在湖面上点 测得塔顶
测得塔顶 的仰角为
的仰角为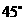 ,沿直线
,沿直线 向塔
向塔 方向前进
方向前进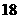 米到达点
米到达点 ,测得塔顶
,测得塔顶 的仰角为
的仰角为 .已知湖面低于地平面
.已知湖面低于地平面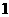 米,请你帮他们计算出塔
米,请你帮他们计算出塔 的高度(结果保留根号).
的高度(结果保留根号).
 答案:解法1:如图,延长
答案:解法1:如图,延长 ,交
,交 的延长线于点
的延长线于点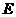
,则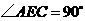 ,
,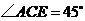 ,
,
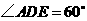 ,
,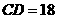 .
.
设线段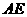 的长为
的长为 米.
米.
在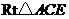 中,
中,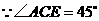 ,
,
 .
.
在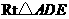 中,
中,
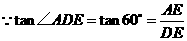 ,
,
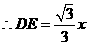 .
.
∵CD=18,且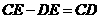 ,
,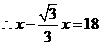 .
.
解得: .
.
∵BE=1米,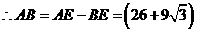 (米).
(米).
答:塔 的高度是
的高度是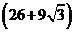 米.
米.
解法2:提示:设塔 的高为
的高为 米.
米.
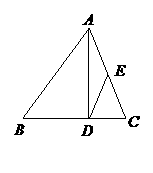
17.(12分)已知:如图,在 中,
中, 是边
是边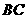 上的高,
上的高,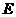 为边
为边 的中点,
的中点,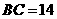 ,
,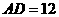 ,
,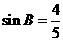 .求(1)线段
.求(1)线段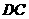 的长;(2)
的长;(2)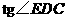 的值.
的值.
 答案:解:(1)在
答案:解:(1)在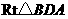 中,
中,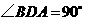 ,
,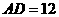 ,
,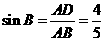 ,
,
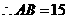 .
.
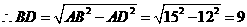 .
.
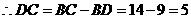 .
.
(2)[方法一]过点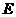 作
作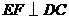 ,垂足为
,垂足为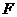 ,
,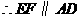 .
.
∵AE=EC,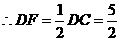 ,
,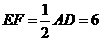 .
.
 在
在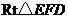 中,
中,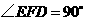 ,
,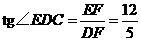 .
.
[方法二]在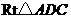 中,
中,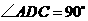 ,
,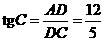 .
.
∵DE是斜边 上的中线,
上的中线,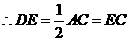 .
.
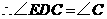 .
.
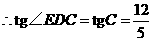 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com