6．★ 已知在一个样本中，50个数据分别落在5个组内，第一、二、三、五组数据的个数分别为2，8，15，5，则第四组的频数和频率分别是________.

5．★★ 某校抽查了50名九年级学生对手足口病三种主要传播途径的知晓情况，结果如下表：

估计该校九年级600学生中，三种传播途径都知道的有　　人.

三种传播途径都知道的有300人．

4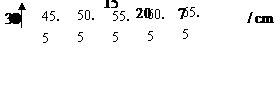． ★ 某校测量了初三(1)班学生的体重(精确到)，按为一段进行分组，得到如下频数分布直方图，则下列说法正确的是(　)

A．该班人数最多的体重段的学生数为7人

B．该班体重低于60.5的学生数为15人

C．该班体重最重段的学生数为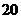人

D．该班体重最重段的学生数为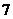人

2．★ 已知样本7，8，10，14，9，7，12，11，10，8，13，10，8，11，10，9，12，9，13，11，那么这组样本数据落在8.5~11.5内的频率是(　　 )

A．0.4　 B．0.5　 C．0.6　 D．0.65

1．★ 某中学对200名年满16岁的男生的身高进行了测量，结果身高(单位：m)在1.68-1.70这一小组的频率为0.25，则该组的人数为　　　　　　　　　　　　　　　　　 (　)

A．60人　 B．15人　 C．50人　 D．25人

2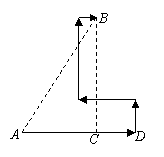．如图所示,某人到岛上去探宝，从A处登陆后先往东走4km，又往北走1.5km，遇到障碍后又往西走2km，再折回向北走到4.5km处往东一拐，仅走0.5km就找到宝藏。问登陆点A与宝藏埋藏点B之间的距离是多少？

解：如图，过点B作BC⊥AD于C，则AC=2.5，BC=6，

由勾股定理求得AB=6.5(km)

1.解：根据题意得：Rt△ADE≌Rt△AEF

∴∠AFE=90°,AF=10 cm,EF=DE

设CE=x cm，则DE=EF=CD－CE=8－x

在Rt△ABF中由勾股定理得：

AB²+BF²=AF²，即8²+BF²=10²，

∴BF=6 cm

∴CF=BC－BF=10－6=4(cm)

在Rt△ECF中由勾股定理可得：

EF²=CE²+CF²，即(8－x)²=x²+4²

∴64－16x+x²=x²+16

∴x=3(cm),即CE=3 cm

1.如图3，已知长方形ABCD中AB=8 cm,BC=10 cm,在边CD上取一点E，将△ADE折叠使点D恰好落在BC边上的点F，求CE的长.

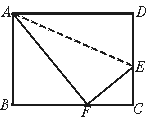
6．解：本题中虽然给出了直角三角形的两边是3、4，而没有指出它们一定是直角边或斜边，所以本题应该分情况讨论。

(1)当3、4，是直角边时，第三边等于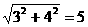

(2)当3与所求的第三边时直角边，4是斜边时，第三边等于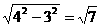

所以本题的答案应该是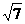或5。

备用题：