
题目列表(包括答案和解析)
1解(1)原式=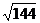 =12
=12
(2)原式=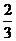 .
.
 2解:本题主要考查学生运用平移和旋转的性质进行作图的能力.如图所示.
2解:本题主要考查学生运用平移和旋转的性质进行作图的能力.如图所示.
3解:甲、乙、丁三位同学的条件均符合要求.
理由:甲从同一底上的两个角进行限定;乙则从对角及邻角之间的关系进行限定,
由于AB∥CD,故∠B+∠C=180°,从而可由∠B+∠D=180°,得∠C=∠D;丁则从对称性进行限定,这些条件都能使梯形ABCD成为等腰梯形.
对于丙的限定,由于∠A+∠D=180°,故∠A=∠D=90°,从而梯形ABCD是直角梯形.
可另外添加∠C=∠D.
4解:(1)猜想AB1∥CB.
 因为△ABC为等腰三角形,所以,由旋转性质知AC=AC1,且△AB1C1也是等腰三角形,所以AB=BC=AB1=B1C.,∠ACB=∠AC1B1=∠B1AC1.
B1
因为△ABC为等腰三角形,所以,由旋转性质知AC=AC1,且△AB1C1也是等腰三角形,所以AB=BC=AB1=B1C.,∠ACB=∠AC1B1=∠B1AC1.
B1
由AC=AC1,得∠AC1C=∠ACB,知∠B1AC1=∠AC1C,所以AB1∥CB.
(2)当∠C=600时,△ABC为等边三角形,同理可得AB1∥CB.
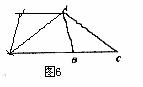
(3)当∠C<600时,如图6所示,同理可得AB1∥CB.
5解:(1)因为MN∥BC,所以∠OEC=∠ECB,∠OFC=∠FCD.又因为CE平分∠ACB,FC平分∠ACD.所以∠ECB=∠OCE,∠OCF=∠FCD,所以∠OEC=∠OCE,∠OFC=∠OCF,所以EO=OC,FO=OC,故EO=FO;
(2)由(1)知,OE=OC=OF,当OC=OA,即点O为AC的中点时,有OE=OC=OF=OA,这时四边形AECF是矩形;
(3)由正方形AECF可知,AC⊥EF,又由于EF∥BC,得∠ACB=90°,所以△ABC是∠ACB=90°的直角三角形.
6解:分两种情况讨论:①若以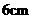 为底,
为底, 为腰,则如图3,在
为腰,则如图3,在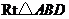 和
和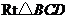 中,分别由勾股定理,得
中,分别由勾股定理,得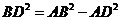
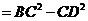 ,
,

 即
即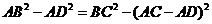 ,所以
,所以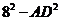
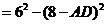 ,即
,即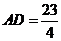 ,所以
,所以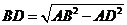 =
=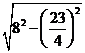 =
=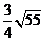 ;②若以
;②若以 为底,
为底, 为腰,则如图4,在
为腰,则如图4,在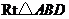 和
和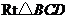 中,分别由勾股定理,得
中,分别由勾股定理,得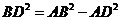
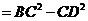 ,即
,即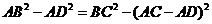 ,所以
,所以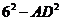
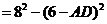 ,即
,即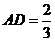 ,所以
,所以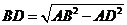 =
=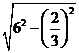 =
=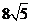 .
.
6.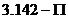 7.17 8.6
9.18 10.等腰或直角或等腰直角三角形
7.17 8.6
9.18 10.等腰或直角或等腰直角三角形
1.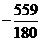 、345.
、345.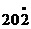 2.< 3.2 4.6、1500 5.9
2.< 3.2 4.6、1500 5.9
1.D 2.A 3.A 4.A 5.C 6.C 7.B 8.C 9.D 10.B
6.已知:等腰三角形中,一边长是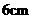 ,另一边是
,另一边是 ,求一腰上的高.
,求一腰上的高.
附答案
5. 如图,△ABC中,点O是AC边上的一个动点,过点O作
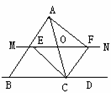 直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角
直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角
平分线于点F.
(1)试探索OE与OF之间的数量关系.
(2)当点O运动到何处时,四边形AECF是矩形,并给出说理
过程.
(3)在(2)的前提下,如果四边形AECF是正方形,那么△ABC将是什么三角形呢?请说明理由.
4.在△ABC中,AB=BC,将△ABC绕点A沿顺时针方向旋转得△A1B1C1,使点Cl落在直线BC上(点Cl与点C不重合).
(1)如图5一①,当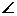 C>60°时,写出边ABl与边CB的位置关系,并加以证明;
C>60°时,写出边ABl与边CB的位置关系,并加以证明;
(2)当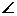 C=60°时,写出边ABl与边CB的位置关系(不要求证明);
C=60°时,写出边ABl与边CB的位置关系(不要求证明);
(3)当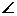 C<60°时,请你在图5一②中用尺规作图法作出△AB1C1(保留作图痕迹,
C<60°时,请你在图5一②中用尺规作图法作出△AB1C1(保留作图痕迹,
不写作法),再猜想你在(1)、(2)中得出的结论是否还成立?并说明理由

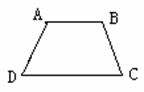
3.已知梯形ABCD,如图所示,其中AB∥CD,现要
求添加一个条件.例如AD=BC,使梯形ABCD是等腰梯形,那么除
了AD=BC外,还可添加一个什么条件,能使梯形ABCD是等腰梯
形?甲、乙、丙、丁四名同学分别添加了一个条件.
甲:∠A=∠B;乙:∠B+∠D=180°;丙∠A=∠D;丁:梯形是轴对称图形.
你认为哪些同学的条件符合要求?理由是 .
你能另外添加一个其他的条件,使梯形ABCD是等腰梯形吗?
2.在下图的正方形网格中有一个直角梯形ABCD,请你在该图中分别按下列要求画出图形(不要求写出画法):
(1)把直角梯形ABCD向下平移3个单位得到直角梯形A1B1C1D1;
 (2)将直角梯形ABCD绕点D逆时针旋转180°后得到直角梯形A2B2C2D.
(2)将直角梯形ABCD绕点D逆时针旋转180°后得到直角梯形A2B2C2D.
图8
1. (1)计算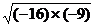 (2)化简
(2)化简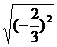
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com