4.1 视角与盲区 同步练习

◆基础训练

20.　　 一枚质量均匀的正方体骰子，六个面上分别标有数字1，2，3，4，5，6，连续抛掷两次．

(1)用列表法或树状图表示出朝上的面上的数字所有可能出现的结果；

(2)记两次朝上的面上的数字分别为p，q，若把p，q分别作为点A的横坐标和纵坐标，求点A(p，q)在函数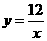的图象上的概率．

19.　　 某商场搞摸奖促销活动：商场在一只不透明的箱子里放了三个相同的小球，球上分别写有“10元”、“20元”、“30元”的字样．规定：顾客在本商场同一日内，每消费满100元，就可以在这只箱子里摸出一个小球(顾客每次摸出小球看过后仍然放回箱内搅匀)，商场根据顾客摸出小球上所标金额就送上一份相应的奖品．现有一顾客在该商场一次性消费了235元，按规定，该顾客可以摸奖两次，求该顾客两次摸奖所获奖品的价格之和超过40元的概率．

18.　　 某中学九年级共有6个班，要从中选出两个班代表学校参加一项重大活动，九(1)班是先进班，学校指定该班必须参加，另外再从九(2)班到九(6)班选出一个班，九(4)班有同学建议用如下方法选班：从装有编号为1，2，3的三个白球的袋中摸出一个球，再从装有编号也为1，2，3的三个红球的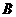袋中摸出一个球(两袋中球的大小、形状与质地完全一样)，摸出的两个球编号之和是几就派几班参加．(1)请用列表或画树状图的方法列举出摸出的两球编号的所有可能出现的结果；(2)如果采用这一建议选班，对五个班是一样公平的吗？请说明理由．

17.　　 小颖和小红两位同学在学习“概率”时，做投掷骰子(质地均匀的正方体)实验，他们共做了60次实验，实验的结果如下：

(1)计算“3点朝上”的频率和“5点朝上”的频率．(4分)

(2)小颖说：“根据实验，一次实验中出现5点朝上的概率最大”；小红说：“如果投掷600次，那么出现6点朝上的次数正好是100次．”小颖和小红的说法正确吗？为什么？(4分)

(3)小颖和小红各投掷一枚骰子，用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率．(4分)

16.　　 一个不透明的口袋里装有红、黄、绿三种颜色的球(除颜色不同外其余都相同)，其中红球有2个，黄球有1个，从中任意摸出1球是红球的概率为．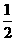

(1)试求袋中绿球的个数；

(2)第1次从袋中任意摸出1球(不放回)，第2次再任意摸出1球，请你用画树状图或列表格的方法，求两次都摸到红球的概率．

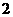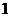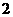15.　　 不透明的口袋里装有红、黄、蓝三种颜色的小球若干个(除颜色外其余都相同)，其中红球个(分别标有号、号)，蓝球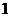个。若从中任意摸出一个球，它是蓝球的概率为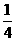.(1)求袋中黄球的个数；(2)第一次任意摸一个球(不放回)，第二次再摸一个球，请用画树状图或列表格的方法，求两次摸到不同颜色球的概率.

14.　　 甲、乙、丙三名学生各自随机选择到A、B两个书店购书．

(1)求甲、乙两名学生在不同书店购书的概率；

(2)求甲、乙、丙三名学生在同一书店购书的概率．

13.　　 将背面相同，正面分别标有数字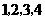的四张卡片洗匀后，背面朝上放在桌面上．

(1)从中随机抽取一张卡片，求该卡片正面上的数字是偶数的概率；

(2)先从中随机抽取一张卡片(不放回)，将该卡片正面上的数字作为十位上的数字；再随机抽取一张，将该卡片正面上的数字作为个位上的数字，则组成的两位数恰好是4的倍数的概率是多少？请用树状图或列表法加以说明．

12.　　 不透明的口袋中装有白、黄、蓝三种除颜色外其余都相同的小球，其中白球1个，黄球2个，蓝球1个，第一次任意摸出一个球不放回，第二次再从中随机摸出一个球，求两次都摸到黄球的概率。