
题目列表(包括答案和解析)
7.方程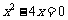 的解是______________.
的解是______________.
6.关于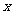 的一元二次方程
的一元二次方程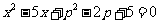 的一个根为1,则实数
的一个根为1,则实数 的值是( )
的值是( )
A.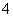 B.
B.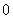 或
或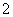 C.
C.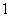 D.
D.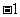
5.用换元法解方程 ,若设
,若设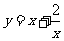 ,则原方程可化为( )
,则原方程可化为( )
(A)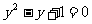 (B)
(B)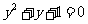
(C)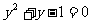 (D)
(D)
4.已知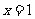 是方程
是方程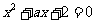 的一个根,则方程的另一个根为( )
的一个根,则方程的另一个根为( )
A. B.
B.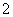 C.
C. D.
D.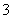
3.方程x2 = x +1的根是( )。
A.x = B. x = C. x =± D. x =
2.用配方法将代数式a2+4a-5变形,结果正确的是( )
A.(a+2)2-1 B. (a+2)2-5
C. (a+2)2+4 D. (a+2)2-9
1.方程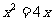 的解是( )
的解是( )
A.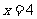 B.
B.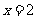
C.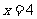 或
或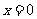 D.
D.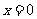
4.求两种函数的解析式的方法是 .
思维扩散
扩散思维是创造思维的重要组成部分,所以通过学习知识,发展扩散思维是十分有益的,使对问题想得宽、想得远、想得细.
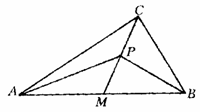
图代13-2-2
例: 如图代13-2-2,在直角三角形ABC中,∠C=90°,已知AC=20cm,BC=15cm.
(1)求AB边上的中线CM的长;
(2)在CM上取一点P(点P与点C、点M不重合),求出△APB的面积y(cm)2与CP的
长x(cm)之间的函数关系式;
(3)在直角坐标系中,画出这个函数图象.
[思考] 1.请你叙述勾股定理.2.直角三角形斜边中线性质你知道吗?
[思路分析] 从条件中不难发现,用勾股定理和直角三角形斜边上的中线定理,很
容求得CM的长,凡有关直角三角形的计算常用勾股定理和锐角三角函数.
解: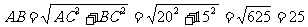 .
.
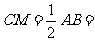 12.5(cm)
12.5(cm)
本例的重点是求解(2),求解这一问方法很多,就求解这一问作如下提示.
[扩散1] 求函数式首先要找到两个变量,本例的两个高精尖量各是什么?哪个量是自变量P点为CM上任一点(P不与C,M重合),即为动点,S△APB是随着P点的变化而变化的,CP的长短是变化的,所以它是什么变量,如何找到S△APB与CP的关系这是关键,从条件和图形应联想到,寻找三角形面积与特定线段的函数关系,即面积的比等于某些线段的比,则想到,“共底不等高的两个三角形面积的比等于高的比”,由此求求.
[思路分析] “共底三角形面积的比等于对应高的比”,那么,它们的高在哪里?在图中找不到,它就暗示必须作出两个三角形的高,这时出现相似三角形,抓住这个契机,便由此可以突破.
解:作PN⊥AB,CD⊥AB,N,D是垂足,
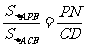
PN∥CD △PMN∽△CMD
△PMN∽△CMD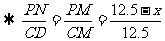
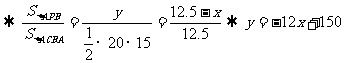 ,
,
从事例的实际出发,CP在0-12.5cm之间变化,∴0<x<12.5.
由于本例寻找的是三角形面积与特定线段之间函数关系,这种解法不止一个,其关键是联想到关定理,“看到图形就能想到它的有关性质”.
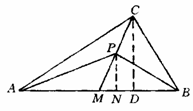
图代13-2-3
[扩散2] 依据定理“等高(或共高)两个三角形面积的比等于两底之比”,
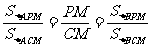 S
S
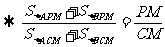
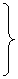
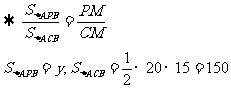
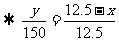
 y=-12x+150.
y=-12x+150.
[扩散3] 依据“三角形中线把原三角形分成面积相等的两个小三角形”,
∵
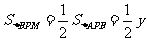 ,
,
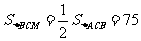 ,
,
∴
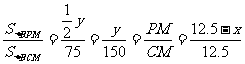 .
.
∴ y=-12x+150.
[扩散4] 应用三角形面积公式,
∵
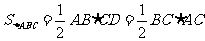
∴
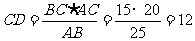 .
.
∵PN⊥AB,CD⊥AB,(见扩散1图代13-2-3)
∴PN∥CD,∴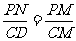 .
.
∴
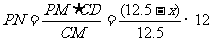 .
.
∵
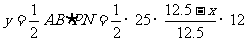 ,
,
∴
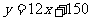 .
.
[扩散5] 依据“遇到中线常加倍”的方法,延长PM到P',且使P'M=PM,则四边形APBP'为平行四边形,S△APP'=S△APB.
∴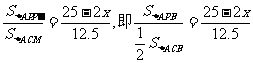 ,
,
∴
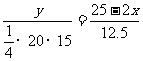 ,
,
∴
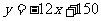 .
.
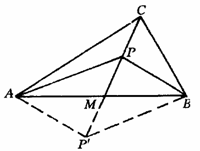
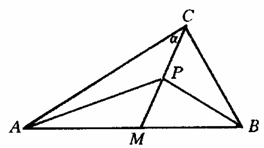
图代13-2-4 图代13-2-5
[扩散6] 遇到直角三角形,可利用锐角三角函数求解.
设∠ACM=α,则∠BCM=90°-α,
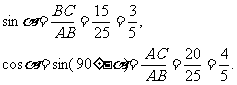
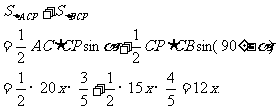
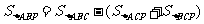
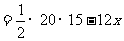 .
.
即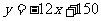 .
.
(3)画图象略.
集中分析
从上例我们可以发现三角形中,等高(或共高)不等底,等底(或共底)不等高特点.三角形这一独特性质是解决三角形面积问题的常用方法,扩散1-2借助它们,思路便疏通了,三角形中线把原三角形面积分成等积的两个三角形的这一性质,使扩散3获得十分简捷解法,对于类似问题都可仿效此法,扩散4借助小学学过的三角形面积公式,也找到了思路,由此可知,三角形面积公式在几何证题中有独到之功,切不可忽视它.今后再遇到类似难题,可以试一试“绝招”,尽管解得有些麻烦,但也可顺利达到目的.扩散5、扩散6的标题已展现出它们的“功劳”.因为,这两种解法很顺畅,尤其扩散6,又开辟证解几何问题的新航道--三角法.请同学们继续进行扩散,还有其他方法.
本例是一道涉及一次函数与几何题的综合题,把数与形交融一体.因而既扬形之可见之长又能发挥数之计算之优,即借助几何原理建立起关系式,再代入数字与字母,应用代数进行化简计算,便可达到目的.只要熟练驾驭数形结合的方法,就能思维扩散自如,数学素养才能提高.
3.两种函数的联系与区别
联系:(1)两种函数都是一条 ;(2)当k>0或k<0时,两函数的增减
性 同;(3)当b=0时,一次函数y=kx+b转化为正比例函数,因此正比例函数可看作一次函数的特例;(4)两种函数的自变量x的指数均为1且k≠0.
区别:(1)正比例函数也是 函数,但是一次函数 是正比例函数;(2)正比例函数的图象一定经过 点,且经过 个象限,一次函数的图象一般不经过 点,且经过 个象限.
2.一次函数的定义、图象、性质
y=kx+b(k≠0)是 函数,其图象是经过两点(0, )和(1, )一条直线.
(1)当k>0时,y随x的增大而 .当k>0,且b>0时,图象经过第 象
限,其示意图是 ;当k>0且b<0时,图象经过第 象限,其示意图是 .
(2)当k<0时,y随x的增大而 .当k<0且b>0时,图象经过第 象限,其示意图是 ;当k<0且b<0时,图象经过第 象限,其示意图是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com