
题目列表(包括答案和解析)
1.3 一元二次方程的应用(3)同步练习
考标要求:
1 会建立一元二次方程模型解决实际问题,并能根据问题的实际意义检验结果的合理性
2 感受数学的应用价值
重点难点:
重点:建立一元二次方程模型解决实际问题;难点:把实际问题化归为一元二次方程
一 填空题(每小题5分,共25分)
1 从正方形的铁片上,截去2cm宽的一条长方形,余下的面积是35 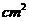 ,那么原正方形铁片的面积是( )
,那么原正方形铁片的面积是( )
A 25 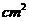 , B 49
, B 49 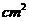 C 81
C 81 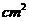 D 36
D 36 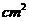
2 用一块长为40cm,宽为30cm的硬纸板,在四个角上截去四个相同的边长为xcm的小正方形,做成底面积为600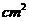 的没有盖的长方体盒子,为求出x ,依题意得方程不正确的是( )
的没有盖的长方体盒子,为求出x ,依题意得方程不正确的是( )
A (40-2x)(30-2x)=600 B 1200-2×40x-2x (30-2x)=600
C 4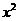 +2x (30-2x)+2×40x) =1200-600
D (40+x) (30+x)=600
+2x (30-2x)+2×40x) =1200-600
D (40+x) (30+x)=600
3 某航空公司有若干个飞机场,每两个飞机场之间都开辟一条航线,一共开辟了15条,则这个航空公司共有飞机场( )
A 4个 B 5个 C 6个 D 7个
4 (2007连云港)为执行“两免一补”政策,某地区2006年投入教育经费2500万元,预计2008年投入3600元,设这两年投入教育经费的年平均增长百分数为x,则可得列方程为( )
A 2500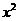 =3600
B
=3600
B 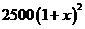 =3600
=3600
C 2500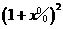 =3600
D
=3600
D 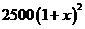 +2500(1+x)=3600
+2500(1+x)=3600
5 (2007吉林) 某中学准备建一个面积为375 的矩形游泳池,且游泳池的宽比长短10m ,设游泳池的长为xm,则可得方程( )
的矩形游泳池,且游泳池的宽比长短10m ,设游泳池的长为xm,则可得方程( )
A x (x-10)=375 B x (x+10)=375 C 2x (2x-10)=375 D 2x (2x+10)=375
二 填空题(每小题5分,共25分)
6已知线段AB=2,点C是AB的黄金分割点,且AC>BC,则线段AC=______
7梯形的下底比上底长3cm,高比上底短1cm,面积为26 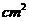 ,如果设上底为
,如果设上底为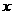 cm,依题意可得方程:_________________
cm,依题意可得方程:_________________
8在一块长方形镜面玻璃的四周镶上与它的周长相等的边框,制成一面镜子。镜子的长与宽的比是2比1。已知镜面玻璃的价格是每平方米120元,边框的价格是每米30元,另外制作这面镜子还需加工费45元。如果制作这面镜子共花了195元,求这面镜子的长和宽。设镜子的宽为x米,依题意得方程______________________________________
9某商品出售价600元,第一次降价后,销售较慢,第二次大幅降价,降价的百分率是第一次的2倍,结果以432元迅速出售,若设第一次降价的百分数为x ,依题意得方程:____________________
10一个容器盛满了纯药液20升,第一次倒出若干升,用水加满,第二次倒出同样多的液体,这时容器里只剩下纯药液5升,若设每次倒出液体x升依题意得方程:_________________
三 解答题(每小题10,共15分)
11某商店如果将进货价为8元的商品按每件10元售出,每天可销售200件,现在采取提高售价,减少进货量的方法增加利润,已知这种商品每涨价0.5元,其销量减少10件,
(1) 要使每天获得700元,请你帮忙确定售价;
(2) 当售价定为多少时,能使每天获得的利润最多?并求出最大利润。
12某市供电公司规定,本公司职工,每户一个月用电量若不超过 千瓦·时,则一个月的电费只要交10元,若超过
千瓦·时,则一个月的电费只要交10元,若超过 千瓦·时,则除了交10元外,超过部分每千瓦/时还要交
千瓦·时,则除了交10元外,超过部分每千瓦/时还要交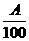 元.一户职工三月份用电80千瓦·时,交电费25元;四月份用电45千瓦·时,交电费10元,试求
元.一户职工三月份用电80千瓦·时,交电费25元;四月份用电45千瓦·时,交电费10元,试求 的值.
的值.
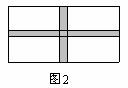
13将一块长18米,宽15米的矩形荒地修建成一个花园(阴影部分)所占的面积为原来荒地面积的三分之二.(精确到0.1m)
(1)设计方案1(如图2)花园中修两条互相垂直且宽度相等的小路.
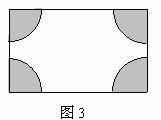
(2)设计方案2(如图3)花园中每个角的扇形都相同.
以上两种方案是否都能符合条件?若能,请计算出图2中的小路的宽和图3中扇形的半径;若不能符合条件,请说明理由.
|
|
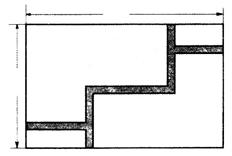 14如图1,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为
14如图1,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为 ,求道路的宽.(部分参考数据:
,求道路的宽.(部分参考数据: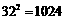 ,
,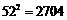 ,
,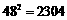 )
)

15 (2006年广东省)将一条长为20cm的铁丝剪成两段,
并以每一段铁丝的长度为周长做成一个正方形.(1)要使这
两个正方形的面积之和等于17cm2,那么这段铁丝剪成两段后
的长度分别是多少?(2)两个正方形的面积之和可能等于12cm2吗? 若能,求出两段铁丝的长度;若不能,请说明理由.
1.3 一元二次方程的应用(1)同步练习
考标要求
1能应用一元二次方程解决简单的代数问题;
2感受一元二次方程的应用价值,提高分析问题解决问题的能力。
重点: 建立一元二次方程模型解决代数问题
难点 根据实际问题建立一元二次模型。
一选择题(每小题5分,共25分)
1 如果代数式: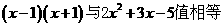 ,则x=( )
,则x=( )
A 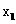 =1,
=1,  =-4 B
=-4 B 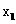 =-1,
=-1,  =4 C
=4 C 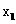 =
=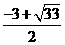 ,
,  =
=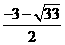
2 要使代数式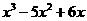 的值等于0,则x的值为( )
的值等于0,则x的值为( )
A 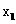 =2
=2  =3 ,
=3 , 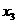 =0 B -2, -3 ,
=0 B -2, -3 , 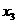 =0, C
=0, C 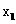 =1
=1  =6,
=6, 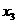 =0 D
=0 D 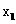 = -1
= -1  = -6,
= -6, 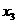 =0
=0
3 当x=1时,代数式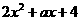 的值为8,当x=-1时这个代数式的值为( )
的值为8,当x=-1时这个代数式的值为( )
A – 8 B 8 C 4 - 4
4 已知一元二次方程 =0,有两个相等的实数根,则k=( )
=0,有两个相等的实数根,则k=( )
A 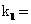 0,
0,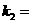 -4,B
-4,B 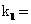 0,
0,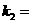 4 C k=4 D k= -4
4 C k=4 D k= -4
5已知关于x的方程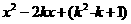 =0有两个相等的实数根,那么关于x的方程
=0有两个相等的实数根,那么关于x的方程
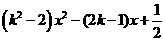 =0的根的情况是( )
=0的根的情况是( )
A 没有实数根 B 有两个不相等的实数根 C 有两个相等的实数根,D 不一定
二 填空题(每小题5分,共25分)
6两个连续奇数的积是323,那么这两个数是_________;
7 若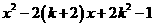 是一个完全平方式,则k=______
是一个完全平方式,则k=______
8 两个函数:y=x-1与y=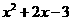 的交点坐标为________________________
的交点坐标为________________________
9 (2006辽宁) 已知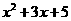 的值是9,则代数式
的值是9,则代数式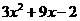 的值为_______
的值为_______
10 已知关于x的方程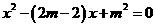 有两个不相等的实数根,那么m的最大整数值是__________
有两个不相等的实数根,那么m的最大整数值是__________
三 解答题(每小题10分,共50分)
11 当x为何值时,代数式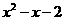 与2x-1值互为相反数
与2x-1值互为相反数
12 (2007福州)若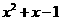 =0,求代数式
=0,求代数式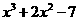 的值
的值
13 一个两位数,十位上的数字比个位上的数字的平方小2,如果把这个数的个位数字与十位数字交换,那么所得到的两位数比原来的数小36,求原来的两位数
14 求证关于x的方程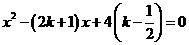 总有实数根
总有实数根
15 (2007成都) 已知x是一元二次方程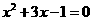 的实数根,那么代数式
的实数根,那么代数式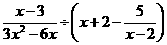 的值为多少?
的值为多少?
四 拓展探究(不计入总分)
16是否存在某个实数m,使得方程 有且只有一个共同根;如果存在,求出这个实数m及两个方程的公共根,如果不存在,说明理由。
有且只有一个共同根;如果存在,求出这个实数m及两个方程的公共根,如果不存在,说明理由。
1.3一元二次方程的应用(2)同步练习
考标要求:
会建立一元二次方程模型解决实际问题,并能根据问题的实际意义检验结果的合理性
重点难点:
重点:建立一元二次方程模型解决实际问题;难点:把实际问题化归为一元二次方程
一 选择题(每小题5分,共25分)
1市政府为了解决市民看病难的问题,决定下调药品的价格。某种药品经过连续两次降价后,由每盒200元下调至128元,这种药品平均每次降价的百分率是( )
A 10% B 15 % C 20 % D 25 %
2 一架长为10米的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为6米,如果梯子的顶端沿墙壁下滑1米,那么梯子的底端向后滑动的距离( )
A 等于1米,B 大于1米,C 小于1米, D 不能确定
3 在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形图.如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )
A.x2+130x-1400=0 B.x2+65x-350=0
C.x2-130x-1400=0 D.x2-65x-350=0
4 某电视机厂计划两年后产量为现在的2倍,如果每年增长率为x,则可得方程( )
A 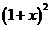 =3, B 1+x=2 C 1+2x=2 D
=3, B 1+x=2 C 1+2x=2 D 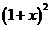 =2
=2
5 借助一面墙为一边,再用13米的铁丝网围成一个面积为20平方米的长方形,求长方形的长和宽,设长为x米,根据题意可得方程( )
A x (13-x)=20
B x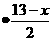 =20 C x (13-0.5x)=20 D
=20 C x (13-0.5x)=20 D 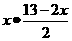 =20
=20
二 填空题(每小题5分,共25分)
6 某印刷厂今年一季度印刷了50万册书,第三季度印刷了72万册书,如果每个季度的增长率相同,设为x,依题意可得方程__________________;
7 某村家用电脑总量,2007年比2005年增长69%,若设平均每年的增长率为x,依题意得方程:______________________;
8 某生活小区准备在每幢楼房之间,开辟面积为200平方米的一块长方形绿地,并且长比宽多10米,则绿地的长为_____米,宽为_______米;
9 用长为24厘米的铁丝围成一个斜边为10cm的直角三角形,则两直角边分别为_______;
10 如图,某小区规划在一个长40米,,宽26米的矩形场地ABCD上修建三条同样宽的小路,使其中两条与AB平行,另一条与BC平行,其余部分种草,若使每一块草坪面积都为144平方米,求小路的宽。设小路宽为x米,依题意得方程:______________________________.
 三 解答题(每小题10分,共50分)
三 解答题(每小题10分,共50分)
11将进货单价为40元的商品按50元售出时,
就能卖出500个.已知这种商品每个涨价1元,
其销售量就减少10个,问为了赚得8000元的利润,
售价应定为多少?这时应进货多少个?
12 读诗词解题:(通过列方程式,算出周瑜去世时的年龄).
大江东去浪淘尽,千古风流数人物;
而立之年督东吴,早逝英年两位数;
十位恰小个位三,个位平方与寿符;
哪位学子算得快,多少年华属周瑜?
13 象棋比赛中,每个选手都与其他选手恰好比赛一局,每局赢者记2分,输者记0分.如果平局,两个选手各记1分,四个同学统计了全部选 手的得分总数,分别是1979,1980,1984,1985.经核实,有一位同学统计无误.试计算这次比赛共有多少个选手参加.
14 春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如图对话中收费标准.

某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元.请问该单位这次共有多少员工去天水湾风景区旅游?
15 (2006年南京市) 西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本共24元.该经营户要想每天盈利200元,应将每千克小型西瓜的售价降低多少元?
17. (本题6分)某校团委准备举办学生绘画展览,为美化画面,在长为30cm、宽为20cm的矩形画面四周镶上宽度相等的彩纸,并使彩纸的面积恰好与原画面面积相等(如图所示),求彩纸的宽度.

16. (本题6分)如图,用一块正方形纸板,在四个角上截去四个相同的边长为2厘米的小正方形,然后把四边折起来,做成一个没有盖的长方体盒子,使它的容积为32立方厘米.所用的正方形纸板的边长应是多少厘米?

15. (本题7分)已知下列n(n为正整数)个关于x的一元二次方程:
(1)方程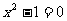 的解为 ;
的解为 ;
方程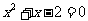 的解为 ;
的解为 ;
方程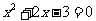 的解为 ;……
的解为 ;……
(2)解关于x的方程: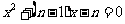 ;
;
14. (本题5分)如果一元二次方程x2+ax +b= 0的两个根是4和-2,则a、b分别等于多少?
13. (本题12分)用适当方法解方程:
(1)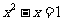 (2)2(2x-3)2-3(2x-3)=0
(2)2(2x-3)2-3(2x-3)=0
(3)3x2-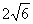 x+2=0
x+2=0
12. (本题16分)解下列方程:
(1)x2-4x+4=0; (2)8y2-2=4y(配方法)
(3)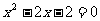 (4)
(4)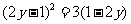
11. 三角形两边长分别为3和6,第三边是方程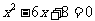 的解,则这个三角形的周长是( )
的解,则这个三角形的周长是( )
A.11 B.13 C.11或13 D.11和13
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com