8．若一个矩形的短边与长边的比值为(黄金分割数)，我们把这样的矩形叫做黄金矩形。

(1)操作：请你在如图20所示的黄金矩形ABCD(AB>AD)中，以短边AD为一边作正方形AEFD；

(2)探究：在(1)中的四边形EBCF是不是黄金矩形？若是，请予以证明；若不是，请说明理由；

(3)归纳：通过上述操作及探究，请概括出具有一般性的结论(不需要证明)。

7．如图18，一天早上，小张正向着教学楼AB走去，他发现教学楼后面有一水塔DC，可过了一会抬头一看：“怎么看不到水塔了？”心里很是纳闷。经过了解，教学楼、水塔的高分别为20m和30m，它们之间的距离为30m，小张身高为1.6m。小张要想看到水塔，他与教学楼的距离至少应有多少m？

6．三国魏人刘徽，自撰《海岛算经》，专论测高望远.其中有一题，

是数学史上有名的测量问题.今译如下：

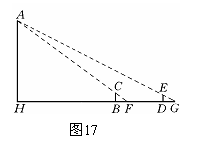如图17，要测量海岛上一座山峰A的高度AH，立两根高三丈的标

杆BC和DE，两竿相距BD＝1 000步，D、B、H成一线，从BC

退行123步到F，人目着地观察A，A、C、F三点共线；从DE退

行127步到G，从G看A，A、E、G三点也共线.试算出山峰的高

度AH及HB的距离.(古制1步＝6尺，1里＝180丈＝1 800尺＝

300步.结果用里和步来表示)

友情提醒：请写出必要的算法和过程。

5.如图16,△ABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F.

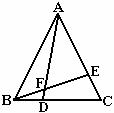(1)试说明△ABD≌△BCE.

(2)△AEF与△ABE相似吗?说说你的理由.

(3)BD²=AD·DF吗?请说明理由.

4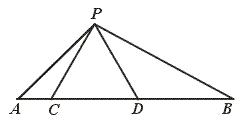．如图15，点C、D在线段AB上，△PCD是等边三角形．

(1)当AC、CD、DB满足怎样的关系时，△ACP∽△PDB？

3.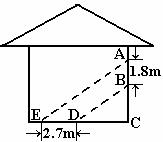阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区(如图14所示),已知亮区到窗口下的墙脚距离EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC.

2．如图13，四边形ABCD、CDEF、EFGH都是正方形.

(1)⊿ACF与⊿ACG相似吗？说说你的理由.

(2)求∠1+∠2的度数.

1．已知一矩形长20cm，宽为10cm，另一与它相似的矩形的一边长为10cm，求另一边长．

10、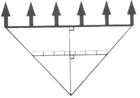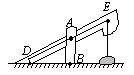如图12所示为农村一古老的捣碎器，已知支撑柱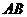的高为 0.3米，踏板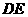长为1.6米，支撑点到踏脚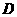的距离为0.6米，现在踏脚着地，则捣头点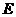上升了　　　　 _________米．