
题目列表(包括答案和解析)
4. ⊙O半径20cm, 弦AB∥CD, AB与CD距离等于4cm, 若AB=24cm, 则CD的长=__________.
3. 在⊙O中, 已知弦AB=m, 弧AB的中点C到AB的距离CD=n, 则圆的半径r为__________.
1.平分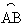 的方法是_____________,它的理论依据是___
的方法是_____________,它的理论依据是___
圆的半径等于4cm,圆内的一条弦长为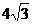 cm,则弦中点与弦所对弧中点的距离等于___________.
cm,则弦中点与弦所对弧中点的距离等于___________.
下列命题中,不正确的是 _________.[ ]
A.垂直于弦的直径平分这条弦
B.平分弦(不是直径)的直径垂直于这条弦
C.弦的垂直平分线是圆的直径
D.平分弦所对的一条弧的直径垂直这条弦
5. 分别过弦的三等分点作弦的垂线.将弦所对的两条弧分别三等分 .( )
4. 在圆中,如果一条直线经过圆心,且平分弦,必平分此弦所对的弧 .( )
3. 平分弦的直线必垂直弦 .( )
2. 平分弧的直径必平分弦 .( )
1. 过圆心平分弦(直径除外)的直线必平分弦所对的两条弧 .( )
3.2.圆的对称性
第1题. 若圆的半径为3,圆中一条弦为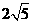 ,则此弦中点到弦所对劣弧的中点的距离为 .
,则此弦中点到弦所对劣弧的中点的距离为 .
答案:1
第2题. 若 是
是 的直径,弦
的直径,弦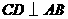 于
于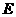 ,
,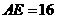 ,
,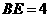 ,则
,则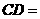 ,
,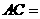 .
.
答案:16 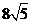
第3题. 已知在 中,
中,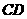 为直径,
为直径, 是弦,
是弦,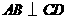 于
于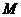 ,
, ,若
,若 ,则
,则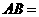 .
.
答案:
第4题. 一条弦 分圆的直径为
分圆的直径为 和
和 两部分,弦和直径相交成
两部分,弦和直径相交成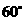 角,则
角,则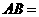 .
.
答案: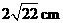
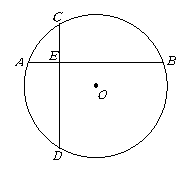 第5题. 如图,在半径为
第5题. 如图,在半径为 的
的 中,弦
中,弦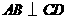 ,垂足为
,垂足为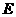 ,若
,若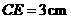 ,
,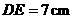 ,则
,则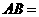 .
.
答案: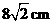
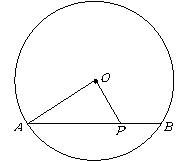
第6题. 如图, 的直径为
的直径为 ,弦
,弦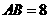 ,
,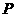 是弦
是弦 上的一个动点,那么
上的一个动点,那么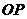 的取值范围是 .
的取值范围是 .
答案: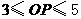
第7题. 在 中,已知
中,已知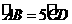 ,那么下列结论正确的是( )
,那么下列结论正确的是( )
A.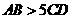 B.
B.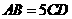 C.
C. D.不确定
D.不确定
答案:C
第8题. 弓形弦长为24,弓形高为8,则弓形所在圆的直径是( )
A.10 B.26 C.13 D.5
答案:B
 第9题. 如图,以
第9题. 如图,以 为圆心的两个同心圆中,大圆的弦
为圆心的两个同心圆中,大圆的弦 交小圆于
交小圆于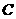 ,
,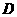 两点,
两点,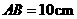 ,
,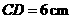 ,那么
,那么 的长为( )
的长为( )
A.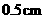 B.
B. C.
C.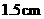 D.
D.
答案:D
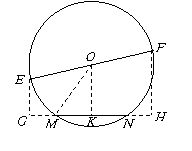 第10题. 如图,
第10题. 如图, 是
是 的直径,
的直径,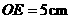 ,弦
,弦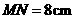 ,则
,则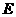 ,
,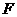 两点到直线
两点到直线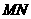 距离的和等于( )
距离的和等于( )
A. B.
B.
C. D.
D.
答案:B
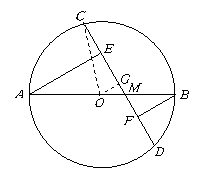 第11题. 如图,
第11题. 如图, 的直径
的直径 与弦
与弦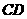 相交于
相交于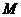 点,
点,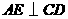 于
于 ,
,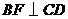 于
于 ,若
,若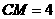 ,
,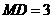 ,
,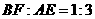 ,则
,则 的半径是( )
的半径是( )
A.4 B.5 C.6 D.8
答案:A
第12题. 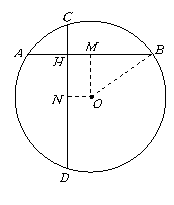 如图,
如图, 的两弦
的两弦 ,
,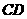 互相垂直于
互相垂直于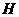 ,
,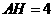 ,
,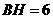 ,
,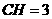 ,
,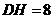 ,求
,求 的半径.
的半径.
答案:过 分别作
分别作 于
于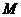 ,
,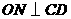 于
于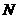 ,得矩形
,得矩形 ,
,
连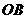 .
.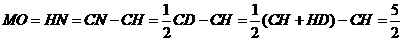 ,
,
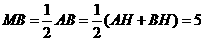 ,Rt△
,Rt△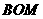 中,
中,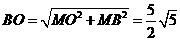 .
.
 第13题. 如图,
第13题. 如图, 的直径
的直径 和弦
和弦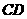 相交于点
相交于点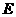 ,已知
,已知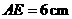 ,
,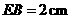 ,
,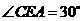 ,求
,求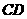 的长.
的长.
答案:过作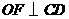 于
于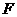 .连
.连 .
.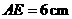 ,
,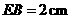 ,
,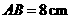 ,
,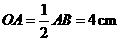 ,
,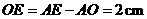 .在Rt△
.在Rt△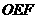 中,
中,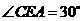 ,
,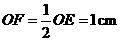 .在Rt△
.在Rt△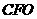 中,
中,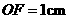 ,
,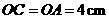 ,
,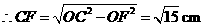 .
.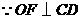 ,
,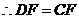 ,
,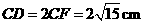 .
.
 第14题. 如图,
第14题. 如图,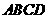 是直角梯形,以斜腰
是直角梯形,以斜腰 为直径作圆,交
为直径作圆,交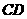 于点
于点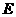 ,
,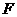 ,交
,交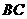 于点
于点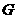 .求证:(1)
.求证:(1)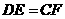 ;(2)
;(2)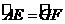 .
.
答案:(1)过 作
作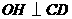 于
于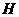 ,则
,则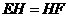 .
.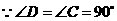 ,
,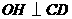 ,
,
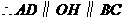 .
.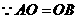 ,
,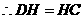 ,
,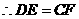 .
.
(2)连 .
.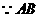 是直径,
是直径,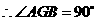 ,
,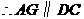 ,
,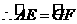 .
.
第15题. 如图,已知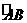 ,在
,在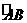 上作点
上作点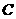 ,
,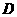 ,
,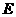 ,使
,使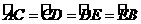 .
.

答案:连 ,作
,作 的垂直平分线交
的垂直平分线交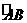 于
于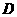 ,连结
,连结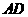 ,作
,作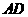 的垂直平分线交
的垂直平分线交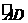 于点
于点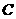 ,同理得
,同理得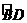 的中点
的中点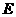 ,即
,即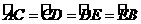 .
.
第16题. 在 中,弦
中,弦 的垂直平分线交
的垂直平分线交 于
于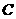 ,
,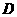 两点,
两点,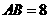 ,弦
,弦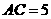 ,求
,求 的直径.
的直径.
答案:设 ,
,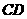 相交于
相交于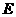 ,在Rt△
,在Rt△ 中,
中,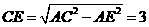 ,连结
,连结 ,得
,得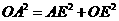 .设
.设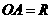 ,则有
,则有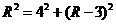 ,
,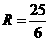 ,
, 的直径为
的直径为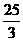 .
.
 第17题. 如图,在
第17题. 如图,在 中,弦
中,弦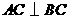 ,若
,若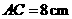 ,
,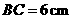 ,则
,则 的半径等于
的半径等于  ,
, 的弦心距等于
的弦心距等于  .
.
答案:5 3
第18题. 如图, 中,
中,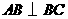 ,
,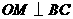 ,
,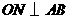 ,垂足分别为
,垂足分别为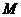 ,
,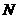 ,若
,若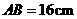 ,
,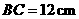 ,则
,则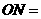
 ,
,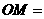
 ,
, 的半径
的半径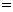
 .
.
答案:6 8 10
 第19题. 如图,在△
第19题. 如图,在△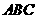 中,
中,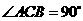 ,
,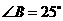 ,以
,以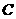 为圆心,
为圆心, 为半径的圆交
为半径的圆交 于
于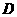 ,交
,交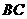 于
于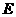 ,则
,则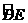 的度数为 .
的度数为 .
答案:
 第20题. 如图,已知
第20题. 如图,已知 中,弦
中,弦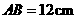 ,
, 点到
点到 的距离等于
的距离等于 的一半,则
的一半,则 的度数为 ,圆的半径为 .
的度数为 ,圆的半径为 .
答案:
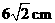
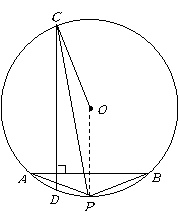
第21题. 如图,已知 的半径为
的半径为 ,
,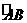 是
是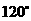 ,那么弦
,那么弦 的弦心距是( )
的弦心距是( )
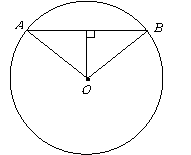 A.
A. B.
B.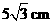
C.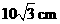 D.
D.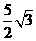
答案:A
 第22题. 如图,
第22题. 如图, 是
是 的弦,从圆上任意一点作弦
的弦,从圆上任意一点作弦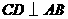 ,作
,作 的平分线交
的平分线交 于点
于点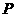 ,若
,若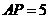 ,则
,则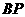 的值为( )
的值为( )
A.4 B.5 C.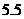 D.
D.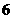
答案:B
第23题. 如图,如果 是
是 的直径,弦
的直径,弦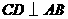 ,垂足为
,垂足为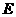 ,那么下面结论中,错误的是( )
,那么下面结论中,错误的是( )
A.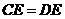 B.
B.
C.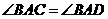 D.
D.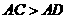

答案:D
第24题. 在半径为5cm的 内有一点
内有一点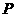 ,若
,若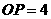 ,过点
,过点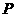 的最大弦长是 cm,过点
的最大弦长是 cm,过点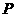 的最短弦的长是 cm.
的最短弦的长是 cm.
答案:10,6
第25题.  的半径为5cm,点
的半径为5cm,点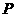 到圆的最小距离与最大距离之比为
到圆的最小距离与最大距离之比为 ,求
,求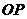 的长.
的长.
答案: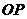 的长是1cm或25cm
的长是1cm或25cm
第26题. 比较下图中的三条弧,先估计它们所在圆的半径的大小关系,再用圆规验证你的结论是否正确.

答案:略
第27题. 已知:如图, 是
是 的直径,
的直径,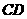 是弦,
是弦,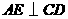 ,垂足是
,垂足是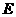 ,
,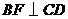 ,垂足是
,垂足是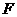 ,求证:
,求证: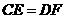 .
.
小明同学是这样证明的: 订正:
证明: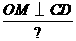
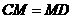
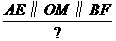
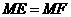
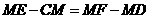
即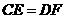
横线及问号是老师给他的批注.许老师还写了如下评语:“你的解题思路很清晰.但证明过程欠完整,相信你思考一下,一定能写出完整的证明过程”.请你帮助小明订正此题,好吗?
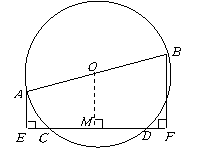
答案:订正:证明:过 作
作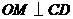 ,垂足为
,垂足为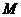 ,则有
,则有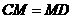 .因为
.因为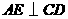 ,
,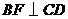 ,所以
,所以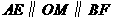 .又因为
.又因为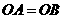 ,所以
,所以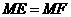 .所以
.所以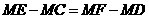 .即
.即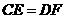 .
.
第28题. 在 中,弦
中,弦 的长恰好等于半径,则弦
的长恰好等于半径,则弦 所对的圆心角为 度,弦
所对的圆心角为 度,弦 所对的圆周角为 度.
所对的圆周角为 度.
答案: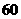 ,
, 或
或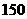
第29题. 圆的一条弦分圆为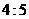 两部分,其中优弧的度数为 .
两部分,其中优弧的度数为 .
答案:
第30题. 同圆中的两条弦长为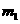 和
和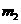 ,圆心到两条弦的距离分别为
,圆心到两条弦的距离分别为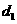 和
和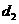 ,且
,且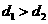 ,那么
,那么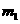 ,
,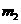 的大小关系是( )
的大小关系是( )
A.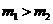 B.
B.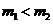 C.
C.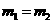 D.
D.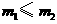
答案:B
第31题. 如图,在 中,
中,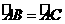 ,
,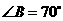 .求
.求 度数.
度数.
答案: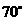
第32题. 如图, 是
是 的直径,
的直径,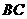 ,
,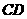 ,
,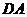 是
是 的弦,且
的弦,且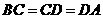 ,求
,求 的度数.
的度数.
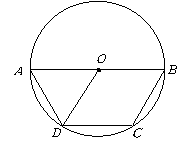
答案: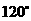
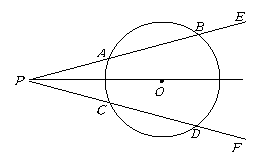
第33题. 如图,点 是
是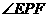 的平分线上的一点,以
的平分线上的一点,以 为圆心的圆和角的两边分别交于点
为圆心的圆和角的两边分别交于点 ,
,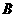 和
和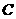 ,
,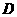 ,
,
(1) 和
和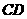 相等吗?为什么?
相等吗?为什么?
(2)若角的顶点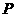 在圆上,或在圆内,本题的结论是否成立?请说明理由.
在圆上,或在圆内,本题的结论是否成立?请说明理由.
答案:(1)相等.作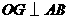 于
于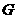 ,
,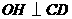 于
于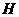 .因为
.因为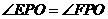 ,所以
,所以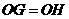 ,所以
,所以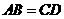
(2)成立(略)
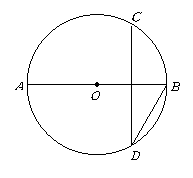
第34题. 如图, 是
是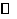 的直径,弦
的直径,弦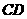 垂直平分
垂直平分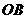 ,则
,则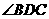 的度数为( )
的度数为( )
 A.
A.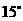 B.
B.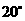
C. D.
D.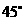
答案:C
第35题.  中
中 是直径,
是直径, 是弦,点
是弦,点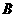 ,
,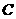 间的距离是2cm,那么圆心到弦
间的距离是2cm,那么圆心到弦 的距离是 cm.
的距离是 cm.
答案:1
第36题. 半径为5cm的圆内有两条互相平行的弦长度分别为6cm和8cm,则这两弦间的距离为 cm.
答案:1或7
 第37题. 如图,
第37题. 如图, 是
是 的直径,
的直径, ,
,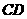 ,
,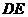 ,
,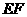 ,
,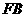 都是
都是 的弦,且
的弦,且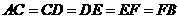 ,求
,求 与
与 的度数.
的度数.
答案: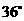 ,
,
第38题. 圆是以 为对称中心的中心对称图形,又是以 为对称轴的轴对称图形.
答案:圆心,过圆心的任一直线.
第39题. 已知 的半径为6cm,
的半径为6cm,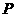 是
是 内一点,
内一点,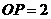 cm,那么过
cm,那么过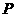 的最短的弦长等于 cm,过
的最短的弦长等于 cm,过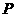 的最长的弦长为 cm.
的最长的弦长为 cm.
答案: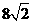 ,12
,12
第40题. 下列命题:①三点确定一个圆,②弦的平分线过圆心,③弦所对的两条弧的中点的连线是圆的直径,④平分弦的直线平分弦所对的弧,其中正确的命题有( )
A.3个 B.2个 C.1个 D.0个
答案:C
 第41题. 如图,
第41题. 如图, 的直径
的直径 垂直于弦
垂直于弦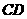 ,
, ,
,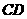 相交于点
相交于点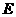 ,
,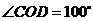 ,求
,求 ,
, 的度数.
的度数.
答案: ,
,
第42题. 如图,有一座石拱桥的桥拱是以 为圆心,
为圆心, 为半径的一段圆弧.
为半径的一段圆弧.
(1)请你确定弧 的中点;(要求:用尺规作图,保留作图痕迹,不写作法和证明)
的中点;(要求:用尺规作图,保留作图痕迹,不写作法和证明)
(2)若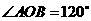 ,
,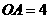 m,请求出石拱桥的高度.
m,请求出石拱桥的高度.
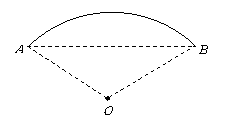
答案:(1)略;
(2)2m.
 第43题. 已知:如图,在同心圆中,大圆的弦
第43题. 已知:如图,在同心圆中,大圆的弦 ,
,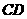 分别与小圆相切于点
分别与小圆相切于点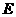 ,
,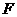 ,则弦
,则弦 ,
,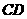 的大小关系是( )
的大小关系是( )
A.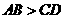 B.
B.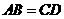
C.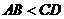 D.无法确定
D.无法确定
答案:B
第44题. 在半径为1的圆中,长为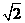 的弦所对的圆心角度数是( )
的弦所对的圆心角度数是( )
A. B.
B.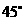 C.
C.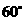 D.
D.
答案:D
第45题. 已知 的半径为
的半径为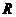 ,弦
,弦 的长也是
的长也是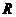 ,则
,则 的度数是 .
的度数是 .
答案: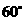
第46题. 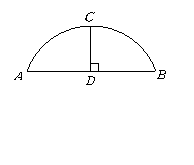 如图,有一圆弧形拱桥,桥的跨度
如图,有一圆弧形拱桥,桥的跨度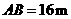 ,拱高
,拱高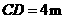 ,则拱桥的半径是 .
,则拱桥的半径是 .
答案:
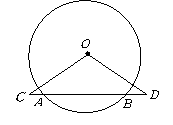 第47题. 如图,已知
第47题. 如图,已知 ,线段
,线段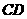 与
与 交于
交于 ,
,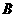 两点,且
两点,且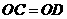 .试比较线段
.试比较线段 和
和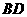 的大小,并说明理由.
的大小,并说明理由.
答案:
 第48题. 如图,在△
第48题. 如图,在△ 中,
中,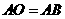 ,以点
,以点 为圆心,
为圆心,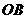 为半径的圆交
为半径的圆交 于
于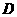 ,交
,交 于点
于点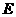 ,
,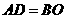 .试说明
.试说明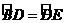 ,并求
,并求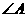 的度数.
的度数.
答案:设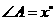 ,
,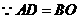 ,又
,又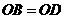 ,
, .
.
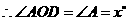 .
.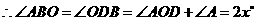 .
.
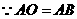 ,
,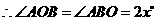 .
.
从而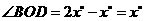 ,即
,即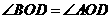 ,
,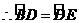 .由三角形的内角和为
.由三角形的内角和为 ,
,
故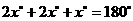 ,
,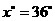 ,即
,即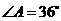 .
.
 第49题. 在直径为
第49题. 在直径为 的圆柱形油槽内装入一些油后,截面如图所示,若油面宽
的圆柱形油槽内装入一些油后,截面如图所示,若油面宽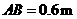 ,则油的最大深度为
,则油的最大深度为  .
.
答案: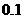
第50题. 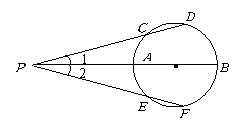 如图,弦
如图,弦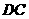 ,
,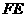 的延长线交于圆外一点
的延长线交于圆外一点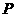 ,
,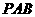 经过圆心,试结合现有图形,添加一个适当的条件 ,使
经过圆心,试结合现有图形,添加一个适当的条件 ,使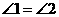 .
.
答案: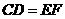
 第51题. 如图,在
第51题. 如图,在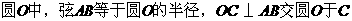 ,则
,则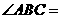 度.
度.
答案:15
第52题. 如图, 的直径,
的直径,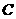 、
、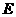 是圆周上关于
是圆周上关于 对称的两个不同点,
对称的两个不同点,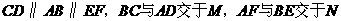 .
.
(1)在 、
、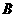 、
、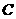 、
、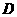 、
、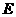 、
、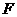 六点中,能构成矩形的四个点有哪些?请一一列出(不要求证明);
六点中,能构成矩形的四个点有哪些?请一一列出(不要求证明);
 (2)求证:四边形
(2)求证:四边形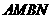 是菱形.
是菱形.
答案:解:(1)能构成矩形的四个点有①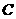 、
、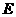 、
、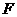 、
、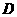 ;②
;② 、
、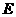 、
、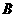 、
、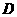 ;
;
③ 、
、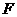 、
、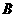 、
、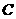 .
.
(2)
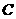 、
、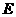 关于直径
关于直径试题详情
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com