
题目列表(包括答案和解析)
2.在同一时刻,一棵高5米的树的影长为2米,此时2米高的小树的影子长为( )
A.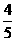 米 B.
米 B.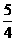 米 C.1米 D.2米
米 C.1米 D.2米
1.小明在某天下午测量了学校旗杆的影子长度,按时间顺序排列正确的是( )
A.6米,5米,4米 B.4米,5米,6米
C.4米,6米,5米 D.5米,6米,4米
3.5平行投影和中心投影
◆基础训练
2.1建立二次函数模型
第1题.
下列函数关系中,可以看作二次函数 模型的是( )
模型的是( )
A.在一定距离内,汽车行驶的速度与行使的时间的关系
B.我国人口自然增长率为1%,这样我国总人口数随年份变化的关系
C.矩形周长一定时,矩形面积和矩形边长之间的关系
D.圆的周长与半径之间的关系
答案:C
第2题. 下列两个量之间的关系不属于二次函数的是( )
A.速度一定时,汽车行使的路程与时间的关系
B.质量一定时,物体具有的动能和速度的关系
C.质量一定时,运动的物体所受到的阻力与运动速度的关系
D.从高空自由降落的物体,下降的高度与下降的时间的关系
答案:A
第3题. 写出下列函数关系式,并指出关系式中的自变量和函数:
圆锥的底面半径为定值r,则圆锥的体积V与圆锥的高h之间的关系
答案: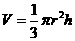
第4题. 已知正方形ABCD中,边长为4,E为AB边上的一动点,(E与A,B点不重合),设AE=x,以E为顶点的内接正方形的面积为y,求y与x的函数关系式,当x为何值时内接正方形的面积最小.
答案: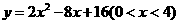 .当
.当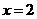 时,内接正方形的面积最小
时,内接正方形的面积最小
第5题. 等边三角形的周长为x,面积为y,用x表示y的关系式为y=_________.
答案: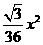
第6题. 当m=_________时,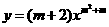 是关于x的二次函数.
是关于x的二次函数.
答案:1
第7题. 写出下列函数的关系式:有一个角是60°的直角三角形的面积S与斜边x的之间的函数关系式.
答案: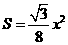
第8题. 一台机器原价60万元,如果每年的折旧率均为x,两年后这台机器的价位约为y万元,则y与x的函数关系式为( )
A.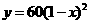 B.
B. C.
C.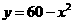 D.
D.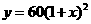
答案:A
第9题.
函数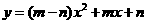 是二次函数的条件是( )
是二次函数的条件是( )
A.m、n是常数,且m≠0 B.m、n是常数,且m≠n
C.m、n是常数,且n≠0 D.m、n可以为任何常数
答案:B
第10题.
一个圆柱的侧面展开图是一个面积为10的矩形,这个圆柱的母线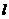 与圆柱的底面半径r之间的函数关系是( )
与圆柱的底面半径r之间的函数关系是( )
A.正比例函数 B.反比例函数 C.一次函数 D.二次函数
答案:B
第11题. 下列不是二次函数的是( )
A.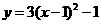 B.
B.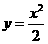 C.
C.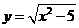 D.
D.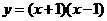
答案:C
第12题.
若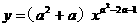 是二次函数,则( )
是二次函数,则( )
A.a=-1或a=3 B.a≠-1,a≠0 C.a=-1 D.a=3
答案:D
第13题. 如果水的流速量 米/分(定量),那么每分钟的进水量Q(立方米)与所选择的水管直径D(米)之间的函数关系是 .其中自变量是 ,常量是 .
米/分(定量),那么每分钟的进水量Q(立方米)与所选择的水管直径D(米)之间的函数关系是 .其中自变量是 ,常量是 .
答案: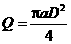 ;D;
;D;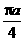
12.如图,在边长为2的正方形ABCD中,P为BC边上的任意一点(点P与B、C不重合),且DQ⊥AP,垂足为Q,设AP=x,DQ=y.
(1)如果连接DP,那么△ADP的面积等于_________;
(2)当点P为BC上的一个动点时,线段DQ也随之变化,若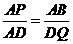 ,求y与x之间的函数关系式,并指出x的取值范围.
,求y与x之间的函数关系式,并指出x的取值范围.
11.下图中有一面围墙(可利用的最大长度为100m),现打算沿墙围成一个面积为120m2的长方形花辅.设花辅的一边AB=x(m),另一边为y(m),求y与x的函数关系式,并指出其中自变量的取值范围.

10.举出生活中变量具有反比例函数关系的实例(1-2例).
[拓展与延伸]
9.已知三角形的面积为100cm2,求三角形的边长y(cm)与该边上的高x(cm)之间的函数关系式,并写出自变量的取值范围.
8.关系式y=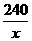 可以表示的实际意义为___________.
可以表示的实际意义为___________.
7.若y与x成反比例,且x=-3时,y=7,则y与x的函数关系式为________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com