
题目列表(包括答案和解析)
8、一张矩形纸片OABC放在平面直角坐标系内,O为原点,点A在x的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.
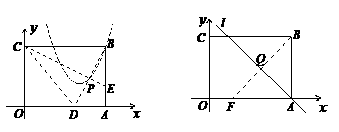
⑴如图①,将纸片沿CE对折,点B落在x轴上的点D处,求点D的坐标;
⑵在⑴中,设BD与CE的交点为P,若点P、B在抛物线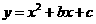 上,求b、c的值;
上,求b、c的值;
⑶如图②,若将纸片沿直线l对折,点B落在坐标轴上的点F处,l与BF的交点为Q,若点Q在的抛物线上,求l 的解析式.
7、如图,已知二次函数图象的顶点坐标为C(1,0),直线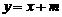 与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴
与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴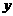 上.
上.
⑴求 的值及这个二次函数的关系式;
的值及这个二次函数的关系式;
⑵P为线段AB上的一个动点(点P与A、B不重合),过P作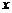 轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为
轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为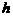 ,点P的横坐标为
,点P的横坐标为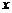 ,求
,求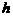 与
与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围;
的取值范围;
⑶D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四形?若存在,请求出此时P点的坐标;若不存在,请说明理由.

6、桂林红桥位于桃花江上,是桂林两江四湖的一道亮 丽的风景线,该桥的部分横截面如图所示,上方可看作是一个经过A、C、B三点的抛物线,以桥面的水平线为X轴,经过抛物线的顶点C与X轴垂直的直线为Y轴,建立直角坐标系,已知此桥垂直于桥面的相邻两柱之间距离为2米(图中用线段AD、CO、BE等表示桥柱)CO=1米,FG=2米.
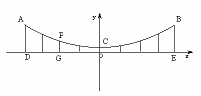 (1)求经过A、B、C三点的抛物线的解析式.
(1)求经过A、B、C三点的抛物线的解析式.
(2)求柱子AD的高度.
5、跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为O. 9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系,设此抛物线的解析式为y=ax2+bx+0.9.
(1)求该抛物线的解析式;
(2)如果小华站在OD之间,且离点O的距离为3米,当绳子甩到最高处时刚好通过他的头顶,请你算出小华的身高;
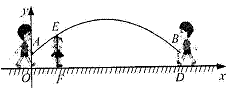 (3)如果身高为1.4米的小丽站在OD之间,且离点O的距离为t米,绳子甩到最高处时超过她的头顶,请结合图像,写出t自由取值范围 .
(3)如果身高为1.4米的小丽站在OD之间,且离点O的距离为t米,绳子甩到最高处时超过她的头顶,请结合图像,写出t自由取值范围 .
4、在直角坐标平面中,O为坐标原点,二次函数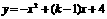 的图象与y轴交于点A,与x轴的负半轴交于点B,且
的图象与y轴交于点A,与x轴的负半轴交于点B,且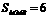 .
.
⑴求点A与点B的坐标; ⑵求此二次函数的解析式;
⑶如果点P在x轴上,且△ABP是等腰三角形,求点P的坐标.
3、某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,具体关系式为:w=-2x+240.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
⑴求y与x的关系式;⑵当x取何值时,y的值最大?
⑶如果物价部门规定这种绿茶的销售单价不得高于90元/千克,公司想要在这段时间内获得2250元的销售利润,销售单价应定为多少元?
2、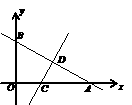 如图,一次函数
如图,一次函数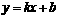 的图象与x轴和y轴分别交于点A(6,0)和B(0,
的图象与x轴和y轴分别交于点A(6,0)和B(0,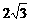 ),线段AB的垂直平分线交x轴于点C,交AB于点D.
),线段AB的垂直平分线交x轴于点C,交AB于点D.
⑴求这个一次函数关系式;⑵求过A、B、C三点的抛物线的函数关系式.
1、在同一直角坐标系中,反比例函数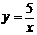 与二次函数
与二次函数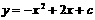 的图象交于点A(-1,m)
的图象交于点A(-1,m)
(1)求m、c的值;(2)求二次函数图象的对称轴和顶点坐标;
5、已知二次函数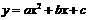 (
(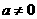 )的图象如上图,有下列4个结论:①
)的图象如上图,有下列4个结论:①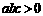 ;②
;②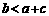 ;③
;③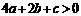 ;④
;④ ;其中正确的结论有( )
;其中正确的结论有( )
A、1个 B、2个 C、3个 D、4个
4、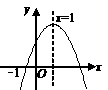 在反比例函数
在反比例函数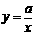 中,当
中,当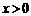 时,
时,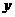 随
随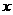 的增大而减小,则二次函数
的增大而减小,则二次函数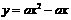 的图象大致是下图中的 ( )
的图象大致是下图中的 ( )
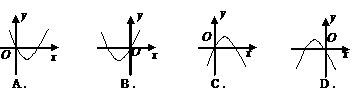
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com