
题目列表(包括答案和解析)
中.只有一项是符合题目要求的)
1.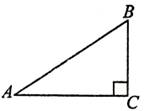 如图,在Rt
如图,在Rt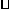 ABC中,
ABC中,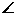 ACB=Rt
ACB=Rt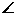 ,BC=1,AB=2,则下列结论正确的
,BC=1,AB=2,则下列结论正确的
是( )
A、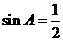 B.
B.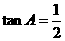
C、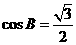 D.
D.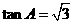
26、已知一次函数y1=-x+6和反比例函数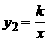 (k≠0)
(k≠0)
(1)k满足什么条件时,这两个函数在同一坐标系中的图象有两个公共点?
(2)给出一个符合(1)的k值,画出这两个函数在同一坐标系中的图象;
(3)设(1)中的两个公共点分别为A、B,∠AOB是锐角还是钝角?
25、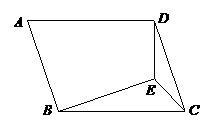 如图,在平行四边形内有一点E满足ED⊥AD于D,∠EBC=∠EDC,
如图,在平行四边形内有一点E满足ED⊥AD于D,∠EBC=∠EDC,
∠ECB=45º,请在图中找出与BE相等的一条线段,并予以证明.
24、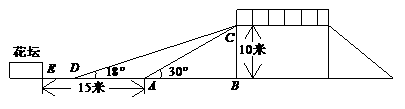 如图,一人行天桥的高是10米,坡面CA的坡角为30°.为了方便行人推车过桥,市政部门决定降低坡度,使新坡面CD的坡角为18°.
如图,一人行天桥的高是10米,坡面CA的坡角为30°.为了方便行人推车过桥,市政部门决定降低坡度,使新坡面CD的坡角为18°.
(A类4分)求新坡长CD.(精确到0.01米)
(B类6分)求原坡脚向外延伸后DA的长. (精确到0.01米)
(C类8分)若需留DE为4米的人行道,问离原坡脚A处15米的花坛E是否需要拆除?
(参考数据sin18°=0.309; cos18°=0.951 ;tan18°=0.325)
附加题:(每小题10分,成绩不记入总分,共20分)
23、妞妞和她的爸爸玩“锤子、剪刀、布”游戏,每次用一只手可以出锤子、剪刀、布三种手势之一,规则是锤子赢剪刀、剪刀赢布、布赢锤子,若两人出相同手势,则算打平.
(1)妞妞和爸爸出相同手势的概率是多少?
(2)妞妞决定这次出“布”手势,妞妞赢的概率有多大?
(3)玩一次游戏,妞妞赢的概率是多少?
(A类5分)完成(1).
(B类6分)完成(1)(2).
(C类7分)完成(1)(2)(3).
22、(A类5分)如图1,平行四边形ABCD中,DE⊥AC,BF⊥AC,垂足分别为E、F,求证:∠ADE=∠CBF.
(B类6分)如图2,在梯形ABCD中,AB∥CD,AD=BC,延长AB到E,使BE=DC,连结AC、CE,求证:AC=CE.
(C类7分)如图3,已知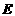 是正方形ABCD的对角线BD上一点,
是正方形ABCD的对角线BD上一点,
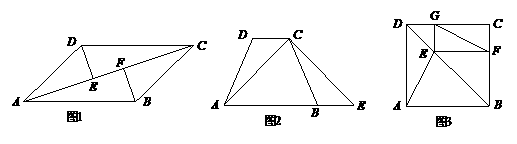 EF⊥BC,EG⊥CD,垂足分别是F、G . 求证:AE=FG..
EF⊥BC,EG⊥CD,垂足分别是F、G . 求证:AE=FG..
.
21、水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
20、如图,一天晚上,李杨在广场上乘凉. 图中线段AB表示站在广场上的李杨,线段PQ表示直立在广场上的灯杆,点P表示照明灯.
(1)请你在图中画出李杨在照明灯P照射下的影子;
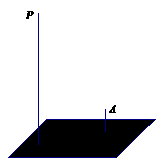 (2)如果灯杆高PQ=12m,李杨的身高AB=1.6m,李杨与灯杆的距离BQ=13m,请求出李杨影子的长度.
(2)如果灯杆高PQ=12m,李杨的身高AB=1.6m,李杨与灯杆的距离BQ=13m,请求出李杨影子的长度.
19、如图,一次函数y1=ax+b(a≠0)与反比例函数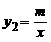 (m≠0)的图象交于P(-2,1)、Q(1,n)两点.
(m≠0)的图象交于P(-2,1)、Q(1,n)两点.
(1)求反比例函数和一次函数的解析式;
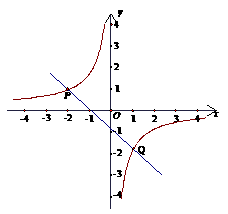 (2)根据图象写出当y1>y2时自变量
(2)根据图象写出当y1>y2时自变量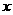 的取值范围.
的取值范围.
18、计算:
(1)sin245°- cos60°+ tan60°cos230° (2)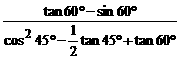
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com